#programming_language

תחשיב למדא

תחשיב למדא הוא צורה לוגית-פורמלית להצגה וטיפול בפונקציות במתמטיקה ומדעי המחשב.

תחשיב למדא הוא מודל חישובי שעל פי תזת צ'רץ'-טיורינג הוא שלם טיורינג כלומר הוא שקול ל מכונת טיורינג .

סימון למדה הוא ביטוי מהצורה $f = λ x . f (x)$ כאשר האיבר אחרי הנקודה הוא כלל התאמה שבדרך כלל מוצג כביטוי של $x$ . למשל את הפונקציה של שורש ריבועי נרשום כך: $λ x . \sqrt{x}$ .

הגדרה:
הביטויים בתחשיב $λ$ מוגדרים באופן הבא:
א) משתנה: $x, y, z$ ... כל משתנה הוא ביטוי.
ב) Abstraction: אם $x$ הוא משתנה ו $t_{1}$ הוא ביטוי אז $λ x . t_{1}$ הוא ביטוי שנקרא ״אבסטרקציה״ לדוגמה: $λ x . x + 1$
ג) Application: אם $t_{1}, t_{2}$ הם ביטויים אז $t_{1} t_{2}$ הוא ביטוי ״הפעלה״ לדוגמה: $(λ x . x + 1) 3$

Note

סוגריים שהושמטו בהפעלות חודרות שמאלה למשל $t_{1} t_{2} t_{3} = (t_{1} t_{2}) t_{3}$

הגדרה:
בביטוי $λ x . t$ כל מופע של $x$ ב $t$ נקרא קשור. $x$ נקרא חופשי אם אינו קשור.
לדוגמה, $x y$ הוא ביטוי שבוא גם $x$ וגם $y$ חופשיים אבל ב $λ y . x y$ מתקיים ש $x$ חופשי ו $y$ קשור

קומבינטור

ביטוי ללא משתנים חופשיים נקרא קומבינטור.

הגדרה:
קומבינטור הזהות הוא $λ x . x$ ונסמנה $i d$ .

כלל אלפה

כלל זה אומר ש $λ x . f (x) = λ y . f (y)$ ומשמעותו הוא ש למדא הוא כמת לוגי קושר. כלומר, מותר לשנות את השם של המשתנה הקשור, כך עוד מחליפים את שמו לשם של משתנה המופיע חופשית.

כלל בתא

רדוקציית $β$ מוגדרת כך:

(λ x . t_{12}) t_{2} \to t_{12} [x \mapsto t_{2}]

כאשר $t_{12} [x \mapsto t_{2}]$ הוא הביטוי המתקבל מ $t_{12}$ על ידי החלפת כל מופע חופשי של $x$ ב $t_{2}$ , זה נקרא substitution .

המשמעות היא שהפעלה של הפונקציה על איבר כלשהו מחזירה את התמונה של אותו איבר לפי כלל ההתאמה של הפונקציה. במילים אחרות, זה כלל הצבה לחישוב הערך שמחזירה הפונקציה.

נשים לב שמחפשים משתנים חופשיים ב $t_{12}$ ולא ב $λ x . t_{12}$ . זה עוזר בהמשך כאשר נתעסק עם למדות שמפעילות למדות אחרות.

דוגמה:
$(λ x . x) y \to y$ , $(λ x . x + 3) 7 \to 10$

בהקשר לנאמר למעלה על ביטויים חופשיים, נסתכל על הדוגמה הבאה $(λ x . x (λ x . x)) (u r)$ .

אנחנו כעת מסתכלים על הביטוי $x (λ x . x)$ ורוצים להפעיל עליו את $u r$ ה $x$ הראשון הוא חופשי אבל הוא מכיל בתוכו ביטוי למדה (שלא הופעל, כלומר יש פה הגדרה של פונקציה פנימית אם נחשוב על זה מנקודת מבט תכנותית) ולכן הפלט יהיה $u r (λ x . x)$ .

תכנות בתחשיב למדא

פונקציה עם כמה ארגומנטים מתנהגים כמו בOCaml :

λ x . λ y . t = λ x . (λ y . t)

ביטויים בוליאניים
הגדרה: הקומבינטורים tru ו fls מוגדרים כך :

\begin{matrix} t r u = λ t . λ f . t \\ f l s = λ t . λ f . f \end{matrix}

במילים אחרות זאת פונקציה שמקבלת שני ארגומנטים ומחזירה את הראשון עבור tru ועבור fls זאת פונקציה שמקבל שני ארגומנטים ומחזירה את השני.

נוכל להגדיר אופרטורים יותר מורכבים למשל $N o t = λ b . b f l s t r u$
הגדרה:
נגדיר את הקומבינטור test להיות

t e s t = λ l . λ m . λ n . l m n

נראה דוגמה

\begin{matrix} test tru v w = (λ l . λ m . λ n . l m n) true v w \to \\ (λ m . λ n . tru m n) v w \to \\ (λ n . tru v n) w \to tru v w \to v \end{matrix}

הפיתוח הוא לפי רדוקציית $β$ עליה דיברנו.

הגדרה:
נגדיר את הקומבינטור and להיות

a n d = λ b . λ c . b c fls

נוכח להוכיח בחלוקה למקרים:
אם $b = t r u$ :
אם $c = t r u e$ אז מפעילים את הפונקציה $tru tru fls$ ונקבל מהגדרה $t r u$ .
אם $c = f a l s e$ אז נריץ את הפונקציה $tru fls fls$ ומהגדרה יוחזר $f l s$ .

המקרה השני כמובן תמיד יחזיר $f a l s e$ .

באופן דומה :

O r = λ b . λ c . b t r u c

הגדרה:
זוגות סדורים

\begin{matrix} pair = λ f . λ s . λ b . b f s \\ first = λ p . p t r u \\ snd = λ p . p f l s \end{matrix}

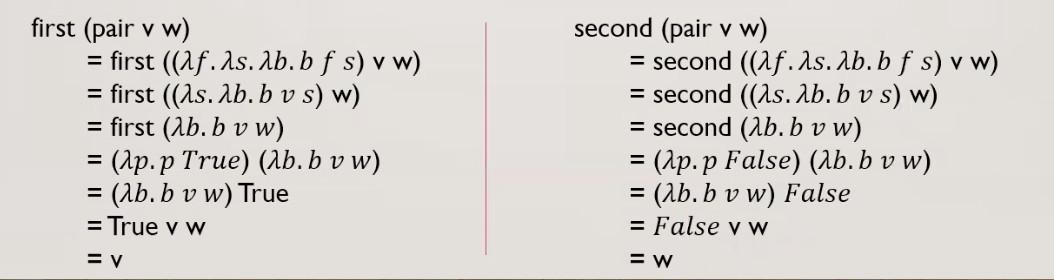
Screenshot 2024-02-13 at 11.51.44.png

pair זאת פונקציה שמקבל שני ארגומנטים ומחזירה פונקציה בוליאנית. אם הקלט אליה הוא tru אז היא תחזיר את f , אחרת היא תחזיר את s. הפונקציות האחרות הן דרך לשלוף את האיבר הראשון/ השני בהתאמה מהזוג הסודר. למשל כדי להוציא את האיבר הראשון נריץ $f i r s t p a i r$ .

הגדרה:
מספרים טבעיים
הקומבינטורים $c_{0}, c_{1}, \dots$ מוגדרים כך

\begin{matrix} c_{0} = λ s . λ z . z \\ c_{1} = λ s . λ z . s z \\ c_{2} = λ s . λ z . s (s z) \\ c_{3} = λ s . λ z . s (s (s z)) \\ ⋮ \end{matrix}

בעצם s היא פונקציית successor ו z זאת פונקציית האפס ועבור $c_{n}$ מפעילים את פונקציית הsuc $n$ פעמים.

הבחנה

הייצוג של $0$ הוא בידיוק כמו הייצוג של $f l s$ ולכן יש שפות תכנות שבהן $0$ מוגדר כ $F a l s e$

נגדיר את פונקציית הsucc : $s u c c = λ n . λ s . λ z . s (n s z)$

בעצם היא מפעילה את $s$ על הפלט מהפעלת $s$ , $n$ פעמים על $z$ .

אריתמטיקה:

p l u s = λ m . λ n . λ s . λ z . m s(n s z)

כאשר $m, n$ אמורים להיות בפועל הקומבינטורים $c_{i}, c_{j}$ כלשהם.

t i m e s = λ m . λ n . m (p l u s n) c_{0}

p o w = λ m λ n . m (times n) c_{1}

מה זה $p l u s n$ ? זאת פונקציה שמקבלת מספר כלשהו ומוסיפה לו את $n$ .

את הפונקציה הזאת מפעילים $m$ פעמים עם הקלט $c_{0}$ וסך הכל מקבלים $m \cdot n$ .

נשתמש בכלים שהגדרנו כדי לכתוב קומבינטור שמקבל מספר ומחזיר tru אם הוא 0 ו fls אחרת:

i s z e r o = λ m . m (λ x . f a l s e) t r u

Pasted image 20240213121445.png

אם $m = c_{0}$ אז הפונקציה תקבל $c_{0}$ תקבל שני ארגומנטים ותחזיר את השני ולכן במקרה הזה מתקבל $t r u$ . כל מקרה אחר יריץ את פונקצית ה succ במקרה הזה $λ x . f a l s e$ שאפשר לראות שלכל $n$ היא מחזירה $f l s$ בסוף.

פתרון לבעיית פיבונצ׳י בתחשיב למדא
הגדרה:

\begin{matrix} z z = p a i r c_{0} c_{0} \\ s s = λ p . p a i r (s n d p) (p l u s c_{1} (s n d p)) \\ p r d = λ m . f s t (m s s z z) \end{matrix}

$z z$ מגדיר את הזוג הסדור $c_{0}, c_{0}$ ו ss מקבלת זוג סדור $p$ ומחזירה זוג סדור כך ש האיבר הראשון הוא האיבר השני ב $p$ והאיבר השני הוא האיבר השני ב $p$ פלוס $1$ .
כעת הפונקציה $p r d$ עושה את החישוב המלא כאשר היא מחזירה את האיבר הראשון מזוג סדור המתקבל מהרצת $s s$ m פעמים עם הקלט ההתחלתי $z z$ .

כעת נוכל להגדיר קומבינטורים אריתמטיים נוספים

s u b = λ m . λ n . n p r d m

כמו כן נוכל להגדיר שיוויון על ידי

e q u a l = λ m . λ n . a n d (i s z e r o (s u b m n) (i s z e r o (s u b m m)))

הסיבה שלעשות רק $i s z e r o (s u b m n)$ לא יעבור היא שהמספרים השליליים לא מוגדרים עבור $s u b$ ולכן זה פשוט יצא עבור מספרים שליליים.

לולאה אינסופית

האתגר כאן הוא קריאה של פונקציה לעצמה שכן לפונקציות אין שם בתחשיב למדה.

לפני שנגדיר נשים לב שעבור הקומבינטור

Ω = (λ x . x x) (λ x . x x)

נקבל שלפי כלל $β$ זה יוצא שהפלט של הפונקציה הוא הפונקציה עצמה כלומר מדובר כאן בלולאה אינסופית.

בעיית העצירה

נזכיר ש בעיית העצירה היא בעיה NPH שמתארת פונקציה וארגומנט ובודקת אם היא עוצרת (מחזירה $t r u$ אם עוצרת ו $f l s$ אם נתקעת):

H a l t = λ f . λ x . /*if f Halt on x /* True False

נניח שזאת פונקצייה אפשרית אזי נגדיר פונקציה חדשה $I s N o t H a l t i n g$ שמקבלת פונקציה ובודקת האם היא לא עוצרת כאשר היא מקבלת את עצמה כארגומנט.

i s N o t H a l t i n g := λ f . H a l t (f, f) (Ω) T r u e

נשים לב שאם f עוצרת על עצמה אז נכנסים ללולאה אינסופית , אם היא לא עוצרת אז הפונקציה מחזירה tru.

כעת נשאל, מה הערך שיוחזר עבור $H a l t (I s N o t H a l t i n g i s N o t H a l t i n g)$ ?

נניח שצריך לחזור אמת כלומר Halt הכריעה שהפונקציה עוצרת על עצמה אבל :

Pasted image 20240213144107.png
בסתירה לכך שחזר true

נניח שזה מחזיר false :
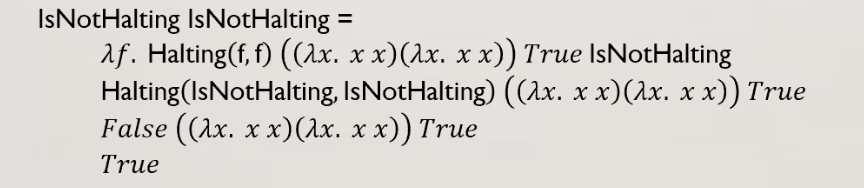
Screenshot 2024-02-13 at 14.46.21.png
בסתירה לכך ש Halt החזירה false

המסקנה היא שלא קיימת פונקציה Halt.

רקורסיה

כעת נגדיר את הקומבינטור Y

r e c = Y = λ f . (λ x . f (x x)) (λ x . f (x x))

למה זה בעצם מהווה רקורסיה?
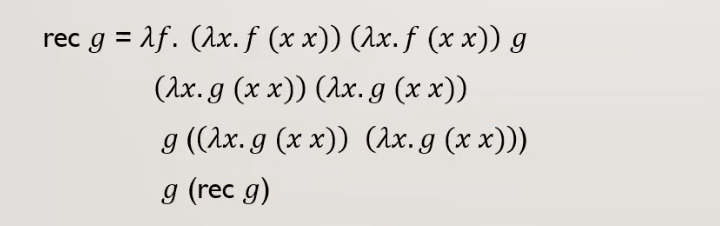
Screenshot 2024-02-13 at 15.58.30.png
בעצם Y מאפשר לנו להעביר כקלט פונקציה אחרת ולהפעיל אותה בצורה אינסופית. על הפונקציה שמעבירים לקבוע מה יהיה התנאי העצירה של הרקורסיה.

למשל נרצה לחשב את פונקציית העצרת: בצורה שהיא לא תחשיבית
למדא טהורה זה היה נראה מהצורה $f a c t = λ f . λ n . if n =1 then 1 else n * f n-1$ .

בצורה שמבוססת רק על תחשיב למדא זה היה נראה כך :

λ f . λ n . test (realeq n c1)c1(times n f pred n)

Screenshot 2024-02-13 at 16.13.27.png

Substitution

יהי $t$ ביטוי. קבוצת המשתנים החופשיים של $t$ מסומנת ב $F v (t)$ ומוגדרת כך

\begin{matrix} F v (x) = {x} \\ F v (λ x . t) = F v (t) - {x} \\ F v (t_{1}, t_{2}) = F v (t_{1}) \cup F v (t_{2}) \end{matrix}

משתנה שמופיע ב $t$ נקרא חופשי ב $t$ אם הוא שייך ל $F v (t)$ וקשור אחרת.

כעת נוכל להגדיר את כללי ה substitution $t [x \mapsto s]$ :

\begin{matrix} x [x \mapsto s] = s \\ y [x \mapsto s] = y \\ (λ y . t_{1}) [x \mapsto s] = λ y . (t_{1} [x \mapsto s]) \\ (t_{1} t_{2}) [x \mapsto s] = (t_{1} [x \mapsto s]) (t_{2} [x \mapsto s]) \end{matrix}

את $(λ y . t_{1}) [x \mapsto s] = λ y . (t_{1} [x \mapsto s])$ מותר לי לעשות רק אם $y$ משתנה שונה מ $x$ ו $y \notin F v (s)$
נשים לב שבלי הדרישה הראשונה נקבל

(λ x . x) [x \mapsto y] = λ x . y

הפכנו קומבינטור לביטוי שאינו קומבינטור.

בלי הדרישה השנייה נקבל

(λ y . x) [x \mapsto y] = λ y . y

כאן הפכנו ביטוי שאינו קומבינטור לקומבינטור.

בצורה יותר מורחבת נקבל:
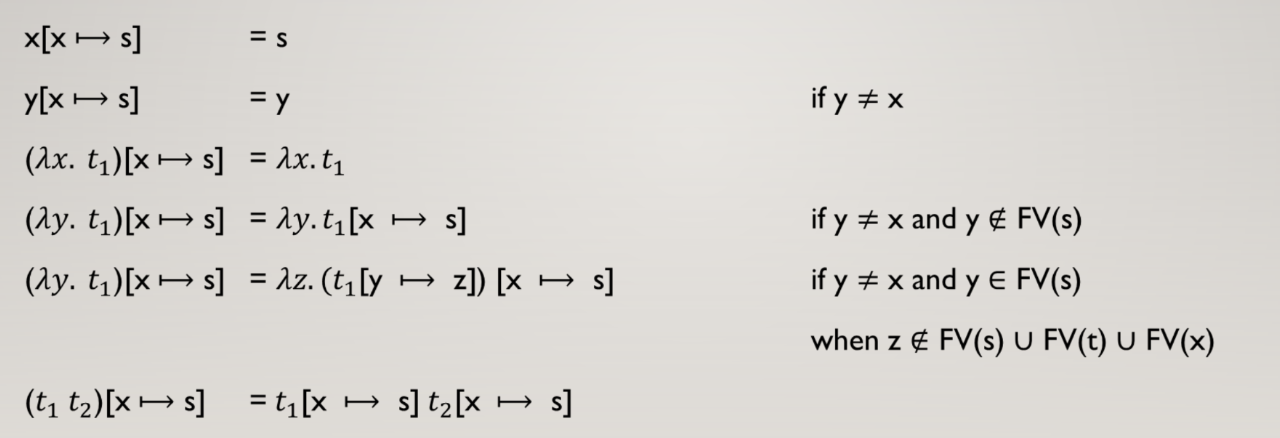
Pasted image 20240325180406.png

סמנטיקה לא דטרמינסטית

הסמנטיקה של רדוקציית בטא היא לא דטרמינסטית למשל :

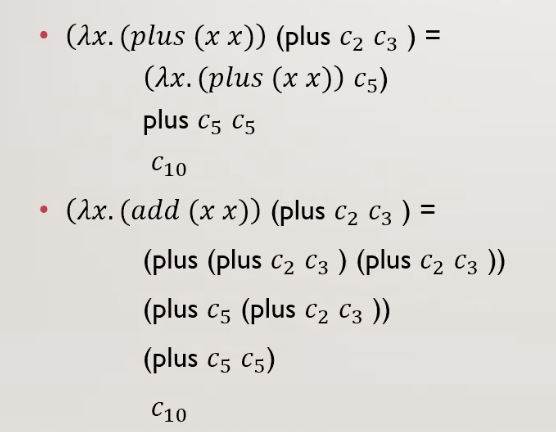
Pasted image 20240213161745.png

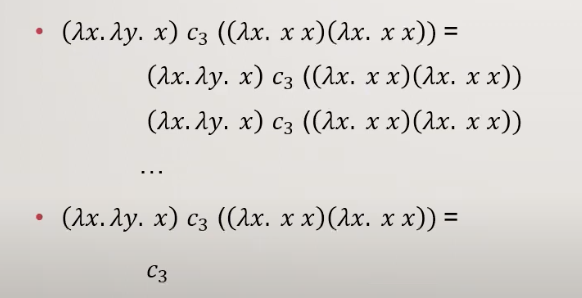
Pasted image 20240213161843.png

כדי להבין מהן השיטות לגשת לבעיות מסוג זה נגדיר קודם כל את המונח רדקס.

הגדרה: ביטוי מהצורה $(λ x . t_{1}) t_{2}$ נקרא רדקס. לעומת זאת, לביטוי מהצורה $λ x . t$ קוראים אבסטרקציה.

\overset{r e d e x}{\overset{⏞}{\underset{a b s t r a c t}{\underset{⏟}{(λ x . t)}} s}}

כמו כן כללי הרדוקציה הקיימים בצורה פורמלית הם
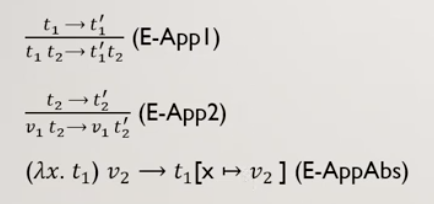
Pasted image 20240213162521.png
הראשון אומר ש אם ניתן לבצע רדוקציית בטא מ $t_{1}$ ל $t_{1}^{'}$ אז הרדוקציית בטא קודם כל תהיה $t_{1} t_{2} \to t_{1}^{'} t_{2}$ כלומר לבצע קודם כל על $t_{1}$ אם ניתן.

השני אומר שאם לא ניתן לבצע על $t_{1}$ את כלל בטא אז צריך לבדוק אם אפשר לבצע על $t_{2}$ .

השלישי אומר שאם מדובר ב״רדקס״ אז מחזירים את $t_{1}$ עם evaluation של $x \mapsto v_{2}$ .

evaluation strategies

כעת ננסה להבין כיצד לקרוא ביטוי מהצורה $(x y) (z w)$ : מספר אסטרטגיות אפשריות:
א) רדוקציה מלאה - אין מגבלות.
ב) סדר נורמלי - מתחילים תמיד עם הרדקס השמאלי ביותר (החיצוני ביותר).
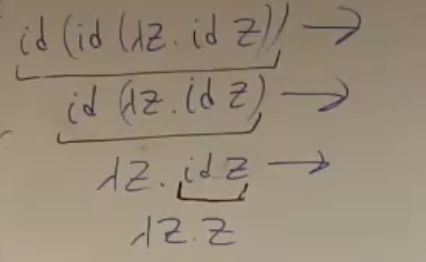
Pasted image 20240211222227.png
ג) call by name - כמו סדר נורמלי אבל לא עושים רדוקצית בטא בתוך אבסטרקציות. כלומר קודם מבצעים השמה ורק אם צריך מחשבים את הביטוי (קדימות ל E-AppAbs)
Pasted image 20240211222239.png
ד) call by value - מותר לבצע רדוקציית בטא על רדקס רק אם צד ימין של הרדקס הוא אבסטרקציה או משתנה. אסור לבצע רדוקציות בתוך אבסטרקציות. כלומר מבצעים השמה רק עבור משתנים ולא ביטויים. (קדימות ל E-App)
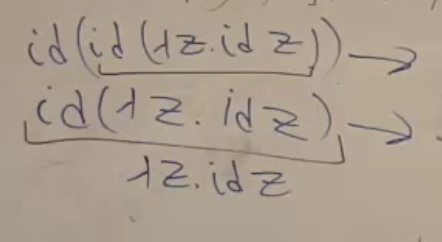
Pasted image 20240211222259.png

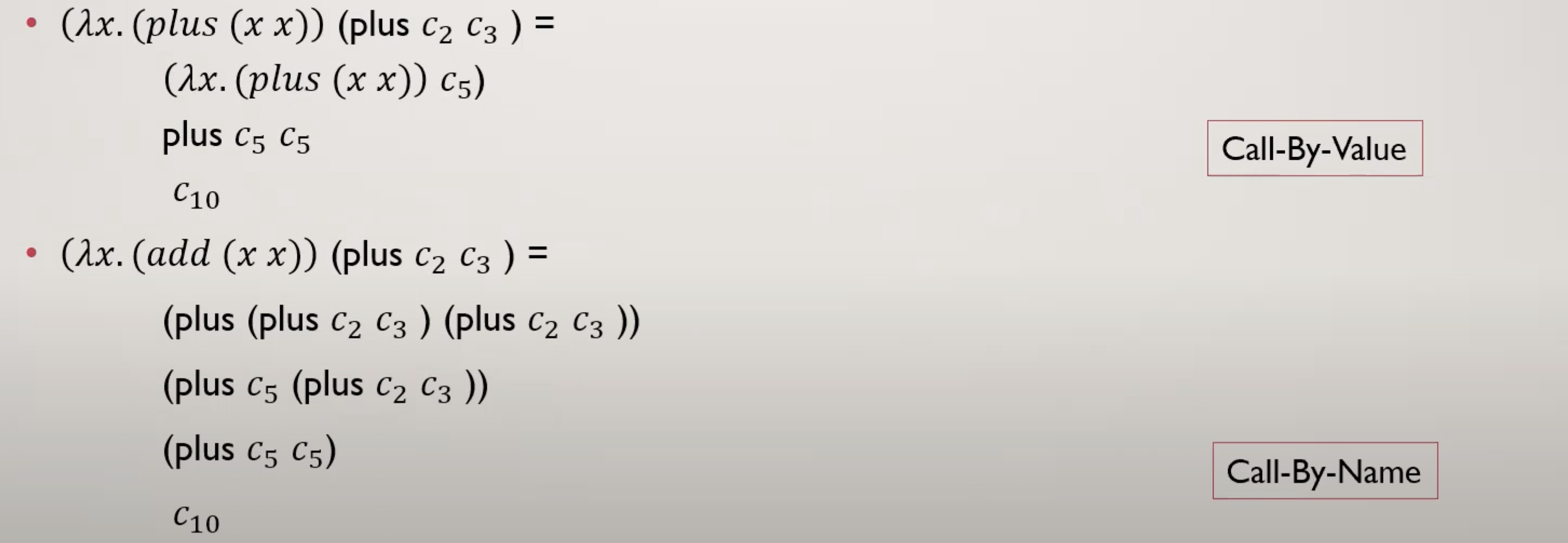
Pasted image 20240227135047.png
ניתן לראות כיצד ב call by value קודם חישבו את ההפעלה ״הפנימית״ ואז החליפו בהפעלה ״החיצונית״ בעוד ש ב call by name קודם ביצעו השמה באבסטרקצייה החיצונית ואז חישבו את ההפעלה הפנימית.

תחשיב למדא עם טיפוסים

בכל השפות תכנות יש תמיכה בטיפוסים. למשל בOCaml על משנה let x = 5 לא נוכל להתייחס כפונקציה. ויש מקרים מורכבים יותר שהקומפילר מצליח לזהות למשל קלט לא תקין לפונקציה.

הקומפילר למעשה לא מריץ התוכנית כדי לגלות את השגיאות הללו. אלא הוא מייצר Abstract Syntax Tree בשלב הראשון ולאחר מכן מבצע Type Checking ו (ישנן שפות כמו אוקמל שעושות גם Type Inference).

נרצה להבין כיצד קומפיילרים מבצעים את הבדיקת טיפוסים הזאת
נשים לב ש type inference זה פיצ׳ר יותר מתקדם מ type checking ולא נתעסק בו כאן.

הגדרה:
קבוצת הטיפוסים מוגדרת כך:
א. Bool
ב. אם $T$ ו $S$ טיפוסים אז $T \to S$ הוא גם טיפוס.

עם ההגדרות האלה ניתן להרחיב את ההגדרות שלנו לטיפוסים נוספים למשל מספרים טבעיים
נגדיר $T :== N a t$ עם החוקים הבאים :
Pasted image 20240215132636.png|300
נשים לב שזה הגדרה לא מדויקת שכן $p r e d 0$ לא משאיר אותנו בטבעיים אבל זה בסדר כי אנחנו יכולים גם להגדיר ש $p r e d 0 = 0$ אם נרצה. כעת נוכל להשתמש בכללי גזירה בסיסיים על הטיפוסים האלה

הגדרה:
ביטויים בתחשיב $λ$ עם טיפוסים מוגדרים כך:
א. כל משתנה הוא ביטוי.
ב. אם $x$ משתנה , $T$ טיפוס ו $t$ ביטוי אז $λ x : T . t$ הוא ביטוי.
ג. אם $t_{1}, t_{2}$ הם ביטויים אז גם $t_{1} t_{2}$
ד. true, false הם ביטויים.
ה. אם $t_{1}, t_{2}, t_{3}$ הם ביטויים אז גם $i f t_{1} t h e n t_{2} e l s e t_{3}$ .

דוגמה: נסמן $i d = λ x : B o o l . x$ ונגדיר
$f = λ x : B o o l \to B o o l . λ y : B o o l x y$
זאת פונקציה שמקבלת ״שני ארגומנטים״ שמפעילה אותם אחד על השני ומחזירה את הפלט הבוליאני (f=test).

נשים לב שההגדרות שלנו עדיין לא מטפלות בטיפוסים למשל $f t r u e i d$ הוא ביטוי תקין לפי ההגדרות שלנו אם כי אנחנו יודעים שהקלט הראשון ל $f$ אמור להיות פונקציה.

הגדרה:
evaluation מוגדר להיות

(λ x : T_{1} . t_{2}) v_{2} \to t_{2} [x \mapsto v_{2}]

i f t r u e t h e n t_{1} e l s e t_{2} \to t_{1}

i f f a l s e t h e n t_{1} e l s e t_{2} \to t_{2}

דוגמה:
נמשיך להסתכל על הפונקציות מהדוגמה הקודמת.

f id true \to true

\begin{matrix} f true id \to (λ x : B o o l \to B o o l . λ y : B o o l . x y) \to (λ y : B o o l t r u e y) i d \\ \to t r u e i d \end{matrix}

true הוא כעת ביטוי בסיסי בשפה ולפי חוקי ה evaluation לא ניתן לפתח את זה ונתקענו עם ביטוי ״בעייתי״ כלומר לפני שהגעתי לערך כלשהו.

הגדרה:
ביטוי ללא משתנים חופשיים נקרא ערך אם הוא $t r u e, f a l s e, λ x : T . t$

הקשרי הטפסה ועצי טיפוסים

הגדרה:
הקשר הטפסה הוא קבוצה של היגדים מהצורה $x : T$ כך $x$ משתנה ו $T$ טיפוס.

נגדיר כעת את יחס ההטפסה להיות

Γ ⊢ t : T

המשמעות של זה באופן אינטואיטיבי היא שהטיפוס של הביטוי $t$ הוא $T$ , תחת ההנחות של הטיפוסים האחרים שנקבעים ביחס $Γ$ שהוא הקשר הטפסה כלשהו .

הביטוי $⊢ t : T$ משמעותו שביטוי $t$ הוא מטיפוס $T$ בסביבה הריקה כלומר בלי הנחות מוקדמות.

Pasted image 20240215152454.png

$⊢$ מוגדר לפי הכללים הבאים :
א. $T - v a r$ : $\frac{x : T \in Γ}{Γ ⊢ x : T}$

ב. $T - T r u e$ $\frac{}{Γ ⊢ t r u e : B o o l}$

ג. $T - F l a s e$ $\frac{}{Γ ⊢ f a l s e : B o o l}$

ד. $T - I F$ $\frac{Γ ⊢ t_{1} : B o o l Γ ⊢ t_{2} : T t_{3} : T}{Γ ⊢ if t1 then t2 else t3:T}$

ה. $T - A P P$ $\frac{Γ ⊢ t_{1} : T_{11} \to T_{12} Γ ⊢ t_{2} : T_{11}}{Γ ⊢ t_{1} t_{2} : T_{12}}$

ו. $T - A B S$ $\frac{Γ, x : T_{1} ⊢ t_{2} : T_{2}}{Γ ⊢ (λ x : T_{1} . t_{2}) : T_{1} \to T_{2}}$
כאשר אין ב $Γ$ ביטוי מהצורה $λ x . . .$ במצב זה מפעילים כלל אלפה. הסימון $Γ, x : T_{1}$ שקול ל $Γ \cup {x : T_{1}}$ .

למשל דוגמה לשימוש בכללי גזירה לפי הקשר הטפסה:
Pasted image 20240215132951.png
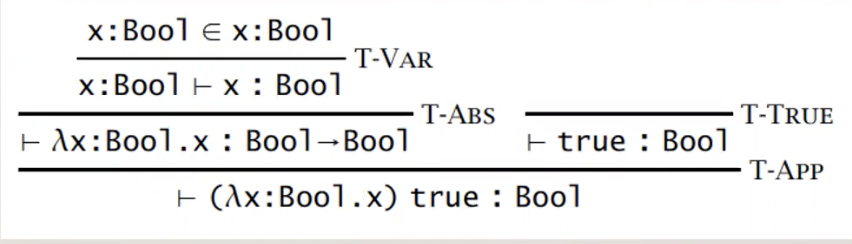
Pasted image 20240215153028.png
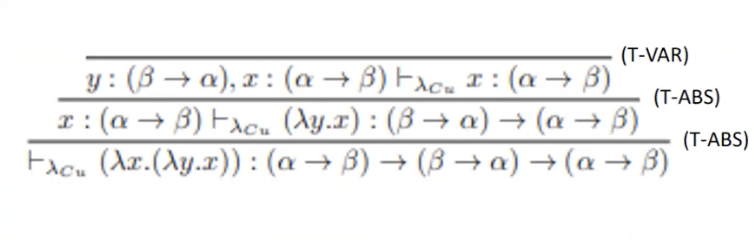
Pasted image 20240215153201.png

נראה דוגמה נוספת על $i d, f$ שהגדרנו למעלה.
נרצה לראות ש $⊢ f i d t r u e : B o o l$ וגם שאין $T$ המקיים $⊢ f t r u e i d : T$ .

Pasted image 20240215153556.png

Pasted image 20240215153948.png

Type Safety

בטיחות סוג ותקינות סוג הן המידה שבה שפת תכנות מרתיעה או מונעת שגיאות סוג. שפות תכנות שונות מגדירות איך לטפל בסתירות או בעיות בהגדרות הסוגים בשפה. כאשר נתקלים בבעיה שכזו, היא תוכל לגרור למשל שגיאה, אזהרה או פשוט התעלמות מהבעיה.

אכיפת סוגים יכולה להיות סטטית, כלומר, לתפוס שגיאות פוטנציאליות בזמן הידור, או דינמית, כלומר לשייך מידע על הסוגים השונים לערכים בזמן ריצה ולהשתמש בסוגים הקיימים לפי הצורך כדי לזהות שגיאות קרובות, או שילוב של שתיהן. אכיפה דינאמית מאפשרת לעיתים קרובות להפעיל תוכניות שיהיו לא חוקיות במסגרת אכיפה סטטית.

Well-typed programs cannot "go wrong". Robin milner

הגדרה:
ביטוי $t$ נקרא מטופס היטב (well-typed program) אם $Γ ⊢ t : T$ עבור $T, Γ$ כלשהם.
הגדרה:
נכתוב $t \to^{*} t^{'}$ אם $t = t_{1} \to t_{2} \to \dots t^{'}$ .

משפט:
אם $t$ ביטוי ללא משתנים חופשיים ומטופס היטב, ו $t \to^{*} t^{'}$ אז $t^{'}$ הוא ערך או שיש $t^{''}$ כך ש $t^{'} \to^{} t^{''}$ .

הוכחה:
ראשית נגדיר את:

למת ההתקדמות: נניח ש $t$ ללא משתנים חופשיים ומטופס היטב אז $t$ ערך או שיש $t^{'}$ כך ש $t \to t^{'}$ .

למת השימור: אם $Γ ⊢ t : T$ ו $t \to t^{'}$ ו $t^{'}$ אינו ערך אז $Γ ⊢ t^{'} : T$
כעת מכיוון ש $t \to^{*} t^{'}$ אז יש $t = t_{1} \to \dots t_{n} = t^{'}$ . נוכיח באינדוקציה על $n$ ש $t_{n}$ הוא ערך או שאפשר להתקדם ממנו וכן ש $t_{n}$ מטופס היטב.

בסיס- $n = 1$ אז $t = t^{'}$ ולכן מטופס היטב ולפי למת ההתקדמות או שהוא ערך או שאפשר להתקדם ממנו.

צעד- $n > 1$ ו $t^{'} = t_{n}$ . אם $t_{n}$ הוא ערך אז סיימנו כי כל הערכים מטופסים היטב. אחרת, לפי הגדרת האינדוקציה $t_{n - 1}$ מטופס היטב ומלמת השימור מתקיים $t_{n}$ מטופס היטב. כמו כן מלמת ההתקדמות מתקיים שניתן להתקדם ממנו.

הוכחת למת ההתקדמות:
באינדוקציה על הגזירה של $Γ ⊢ t : T$ (קיימים כאלה כי $t$ מטופס היטב).

בסיס: אם הכלל הוא $T - T r u e$ או $T - F a l s e$ אז $t$ הוא ערך.
לא יתכן שהכלל הוא $T - V a r$ כי ב $t$ אין משתנים חופשיים.

צעד: עבור $T - A B S$ אז $t$ הוא אבסטרקציה ולכן ערך.
אם $T - A P P$ אז $t = t_{1} t_{2}$ עבור $t_{1}, t_{2}$ כלשהם. לפי הכלל מתקיים ששניהם מטופסים היטב ולפי הנחת האינדוקציה או שהם ערכים או שניתן להתקדם מהם לפי המקרים הבאים
א. $t_{1}$ ניתן להתקדם ל $t_{1}^{*}$ ובמקרה כזה $t_{1} t_{2} \to t_{1}^{*} t_{2}$
ב. אם ניתן להתקדם מ $t_{2}$ זה כמו סעיף א.
ג. אם שניהם ערכים אז $Γ ⊢ T_{11} \to T_{12}$ לפי הכלל. לכן
$$t_{1}=\lambda x: T_{11}.t_{12}$$
עבור $x, t_{12}$ כלשהם.

כלומר $t_{1} t_{2} = (λ x . T_{11} : t_{12}) t_{2} \to t_{12} [x \mapsto t_{2}]$ וכך התקדמנו.

עבור $T - I F$ נקבל הוכחה דומה.

הוכחת למת השימור:
נוכיח באינדוקציה על הגזירה של $Γ ⊢ t : T$ .
בסיס:
1) אם T-true אז t ערך
2) כנ״ל לגבי T-false
3) T-VAR אז t משתנה ולכן $t ↛ t^{'}$ .

צעד:
1) T-ABS אז t ערך
2) T-IF יהיה דומה ל T-APP
3) T-APP

\frac{Γ ⊢ t_{1} : T_{11} \to T_{12} Γ ⊢ t_{2} : T_{11}}{Γ ⊢ t_{1} t_{2} : T_{12}}

כך ש $t = t_{1} t_{2}$ וגם $t_{1} = λ x : T_{11} . t_{11}$ ולכן $t^{'} = t_{11} [x \mapsto t_{2}]$ .

נרצה להוכיח ש $Γ ⊢ t_{11} [x \mapsto t_{2}] : T$ כיוון שהנחת האינדוקציה שלנו היא על $t_{1}$ ולא על $t_{11}$ ולכן נתקענו כרגע.

כדי להמשיך את ההוכחה נשתמש ב-

למת ההחלפה:
אם $Γ, x : S ⊢ t : T$ וגם $Γ ⊢ s : S$ אז $Γ ⊢ t [x \mapsto s] : T$ .
במילים, זה אומר שאם נבצע החלפה בין משתנים מאותו טיפוס, הביטוי עדיין נשאר באותו טיפוס.

נוכיח באינדוקציה על עץ הגזירה של $Γ, x : S ⊢ t : t$ .
בסיס:
1) T-TRUE אז t=true כלומר T=Bool ולכן $t [x \mapsto s] = t r u e$ ולכן מתקבל הדרוש.
2) T-FALSE דומה ל1.
3) T-VAR אז t משתנה. נחלק ל2 מקרים
* $t = x$ אז $S = T$ ו $t [x \mapsto s] = s$ . וכבר ידוע ש $Γ ⊢ s : S$ .
* $t$ משתנה אחר ואז $t [x \mapsto s] = t$ ואז נפעיל את T-VAR ונקבל את הדרוש.

צעד:
א) T-APP. אז $\frac{Γ, x : S \to t_{1} : T_{11} \to T_{12} Γ . x : S ⊢ t_{2} \to T_{11}}{Γ, x : S ⊢ t_{1} t_{2} : T_{12}}$

נרצה להראות ש $Γ ⊢ (t_{1} t_{2}) [x \mapsto s] : T_{12}$ כלומר $Γ ⊢ t_{1} [x \mapsto s] t_{2} [x \mapsto s] : T_{12}$ .

לפי הנחת האינדוקציה מתקיים ש $Γ ⊢ t_{1} [x \mapsto s] : T_{11} \to T_{12}$ וגם $Γ ⊢ t_{2} [x \mapsto s] : T_{11}$

נפעיל שוב את T-APP ונקבל

\frac{Γ ⊢ t_{1} [\mapsto s] : T_{11} \to T_{12} Γ ⊢ t_{2} [x \mapsto s] : T_{11}}{Γ ⊢ t_{1} [x \mapsto s] t_{2} [x \mapsto s] : T_{12}}

שזה בידיוק מה שרצינו להוכיח.

ב) T-ABS :

\frac{Γ, x : S, y : T_{1} ⊢ t_{2} : T_{2}}{Γ, x : S ⊢ λ y : T_{1} . t_{2} : T_{1} \to T_{2}}

כאשר נסמן $t = λ y : T_{1} . t_{2}$ ו $T = T_{1} \to T_{2}$ .
לפי הנחת האינדוקציה מתקיים $Γ, y : T_{1} ⊢ t_{2} [x \mapsto s] : T_{2}$ אם נפעיל את T-ABS כעת נקבל את הדרוש.

\frac{Γ, y : T_{1} ⊢ t_{2} [x \mapsto s] : T_{2}}{Γ ⊢ λ y : T_{1} . t_{2} [x \mapsto s] : T_{1} \to T_{2}}

ג) T-IF דומה.

כעת נוכל לחזור להוכחה של למת השימור רצינו להראות ש: $Γ ⊢ t_{11} [x \mapsto t_{2}] : T$ לאחר שהפעלנו T-APP:

\frac{Γ ⊢ t_{1} : T_{11} \to T_{12} Γ ⊢ t_{2} : T_{11}}{Γ ⊢ t_{1} t_{2} : T_{12}}

והסברנו ש $t = t_{1} t_{2}$ וגם $t_{1} = λ x : T_{11} . t_{11}$ ולכן $t^{'} = t_{11} [x \mapsto t_{2}]$ .

מלמת ההחלפה די להראות
א) $Γ ⊢ t_{2} : T_{11}$
ב) $Γ, x : T_{11} ⊢ t_{11} : T_{12}$

הסעיף הראשון ידוע מהנחות הכלל T-APP.
לגבי ב׳ , ידוע ש $Γ ⊢ t_{1} : T_{11} \to T_{12}$

ניתן לקבל זאת רק משימוש ב T-ABS

\frac{Γ, x : T_{11} ⊢ t_{11} : T_{12}}{Γ ⊢ λ x : T_{11} . t_{11} : T_{11} \to T_{12}}

שזה בידיוק מה שרצינו להוכיח.

נורמליזציה

נגדיר ביטוי t כמנתנרמל אם יש ערך $t^{'}$ כך ש $t \to^{*} t^{'}$ .
כעת, משפט הנורמליזציה אומר ש-
אם ב t אין משתנים חופשיים ו $⊢ t : T$ אז $t$ מתנרמל.

הוכחה:
כדי להוכיח את המשפט נניח שהאסטרטגה היא CBV. כעת, נגדיר עבור טיפוס T את הקבוצה $R_{T}$ באופן הבא:
* $R_{B o o l}$ היא קבוצת כל הביטויים מטיפוס Bool שמתנרמלים
* $R_{T_{1} \to T_{2}}$ היא קבוצת כל הביטויים t מטיפוס $T_{1} \to T_{2}$ שמתנרמלים ובנוסף לכל ביטוי $s \in R_{T_{1}}$ מתקיים ש $t s \in R_{T_{2}}$ .

דוגמה:
$(λ x : B o o l . x) t r u e : R_{B o o l}$

למה: אם $Γ t : T$ ו $t \to t^{'}$ אז $t^{'} \in R_{T} \leftrightarrow t \in R_{T}$
נוכיח באינדוקציה על T.
בסיס:
T=Bool :
$\leftarrow$ נניח $t \in R_{B o o l}$ . מלמת השימור $⊢ t^{'} : B o o l$ . מכיוון שאנו בCBV ו t מתנרמל, גם $t^{'}$ מתנרמל
$\to$ דומה (פשוט יותר)

צעד:
$T = T_{1} \to T_{2}$
$\leftarrow$ נניח ש $t \in R_{T}$ כמו קודם, ברור ש $t^{'}$ מתנרמל ומטיפוס T.
יהי $s \in R_{T_{2}}$ . נרצה להוכיח ש $t^{'} s \in R_{T_{2}}$ .
$t \in R_{T}$ ולכן $t s \in R_{T_{2}}$ . מכיוון ש $t \to t^{'}$ אז גם $t s \to t^{'} s$ הטיפוס של שניהם הוא $T_{2}$ ולפי הנחת האינדוקציה כיוון ש $t s \in R_{T}$ נקבל שכך גם $t^{'} s$
$\to$ דומה.

כעת כדי להוכיח את הטענה הקודמת, נכליל את הטענה ונניח כי

x_{1} : T_{1}, \dots, x_{n} : T_{n} ⊢ t : T

ו $v_{1} \dots v_{n}$ ערכים מטיפוסים $T_{i}$ בהתאמה כך שלכל i מתקיים $v_{i} \in R_{T_{i}}$ אז

t^{'} := t [x_{1} \mapsto v_{1}] [x_{2} \mapsto v_{2}] \dots [x_{n} \mapsto v_{n}] \in R_{T}

הוכחה:
באינדוקציה על עץ הגזירה. המקרה המעניין היחיד הוא T-ABS כאשר $t = λ x : S_{1} . t_{2}$ .

ברור ש $t^{'}$ ערך ולכן מתנרמל. יהי $s \in R_{S_{1}}$ . נוכיח ש $t^{'} s \in R_{S_{2}}$ . מהגדרת $R_{S_{1}}$ $s \to^{*} v$ עבור v ערך כלשהו. מהלמה הקודמת $v \in R_{S_{1}}$ ולפי האנחת האינדוקציה $t_{2} [\dots] \dots [\dots] \in R_{S_{2}}$ אבל זה בידיוק מה שנקבל מ ts.

נשים לב: עבור n=0 קיבלנו מיד את משפט הנורמליזציה לפי הגדרת $R_{T}$

הבחנה

המשמעות של משפט זה היא שתחשיב $λ$ עם טיפוסים זה מודל מאוד חלש שכן ברוב שפות התכנות הקיימות התכונה הזאת לא מתקיימת (התכונה במובנים תכנותיים היא שהקומפיילר ידע לזהות טיפוסים כך שלא נתקע או נכנס ללולאה אינסופית בזמן קומפילציה)

Curry Howard Isomorphism

שימוש חשוב ל typed lambda expression הוא CHI. הרעיון הוא שניתן להוכיח פסוקיות לוגיות בעזרת חישוב בתחשיב למדא עם טיפוסים:
א) ניתן לייצר משתנים בלוגיקה פסוקית כטיפוסים.
ב) הוכחה היא פונקציה.
ג) נייצג אופרטורים לוגיים בעזרת תחשיב למדא על טיפוסים.

ניתן להשתמש בתחשיב למדא כמערכת הוכחה ללוגיקה פסוקית כאשר כל פרדיקט מהווה איזשהו טיפוס.

Screenshot 2024-02-15 at 15.57.26.png|300

נסתכל על הביטוי הבא

P \land (Q \lor R) \to (P \land Q) \lor (P \land R)

משפט זה הוא תיאותולוגיה (פסוק שהוא תמיד אמת). ניתן להוכיח שהוא תיאותולוגיה בעזרת בניית פונקציה $f$ כך ש

f : P + (Q \times R) \to (P + Q) \times (P + R)

כעת נוכל להראות שזה תיאותולוגיה אם נראה עת גזירה שמראה שהטיפוס של $f$ הוא אמת.