אמידה סטטיסטית נקודתית
דיברנו על הגשר מתורת ההסתברות אל הההסקה הסטטיסטית .
כעת נרצה לדבר על התאוריה שמשתמשת בתורת ההסתברות כדי להסיק מסקנות לגבי האוכלוסייה מתוך התוצאות של מדגם תצפיות.
אחד הנושאים המרכזיים של הסקה סטטיסטית הוא, אמידה של מאפיינים שונים של האוכלוסייה שבוא נתעסק בסיכום זה.
עקרונות של אמידה
במקרים רבים נרצה לדעת את ערכו של פרמטר מסוים באוכלוסייה. בגלל גודלה של האוכלוסייה איננו יכולים לחשב אותו ואנו נאלצים להתבסס על הסטטיסטי המתאים במדגם מקרי מתוך אותה אוכלוסייה. תהליך זה נקרא אמידה.
דוגמה לבעיה של אמידה היא למשל , אמידה של ההסתברות להצלחה של טיפול רפואי באמצעות מדגם של חולים שיקבלו את הטיפול.
בכל בעיית אמידה נרצה לאמוד מדד מסוים של המשתנה המקרי הנבדק או של האוכלוסייה הנבדקת. מדד זה נקרא פרמטר.
פרמטר של פונקציית ההתפלגות של מ״מ הוא ערך הנקבע על ידי התפלגות זו, ומהווה אחד המאפיינים שלה.
הפרמטרים החשובים ביותר של מ״מ שדיברנו עליהם הינם התוחלת והשונות של משתנה מקרי:
פרמטר חשוב נוסף שנאמוד בקורס הוא הפרמטר
כיצד אומדים פרמטר?
בעזרת סטטיסטי מתאים.
סטטיסטי הוא ביטוי מתמטי מוגדר (פונקציה) של תצפיות המדגם
נסמן ב
במקרה זה נאמר כי
הכוונה היא שהערך שיקבל המשתנה המקרי
למשל, עבור התוחלת
הערך ש
פרמטר הוא מספר קבוע, ואילו האומד שלו
נזכיר ש התפלגות הדגימה היא פונקציית ההסתברות של סטטיסטי כלשהו. גם לאומד
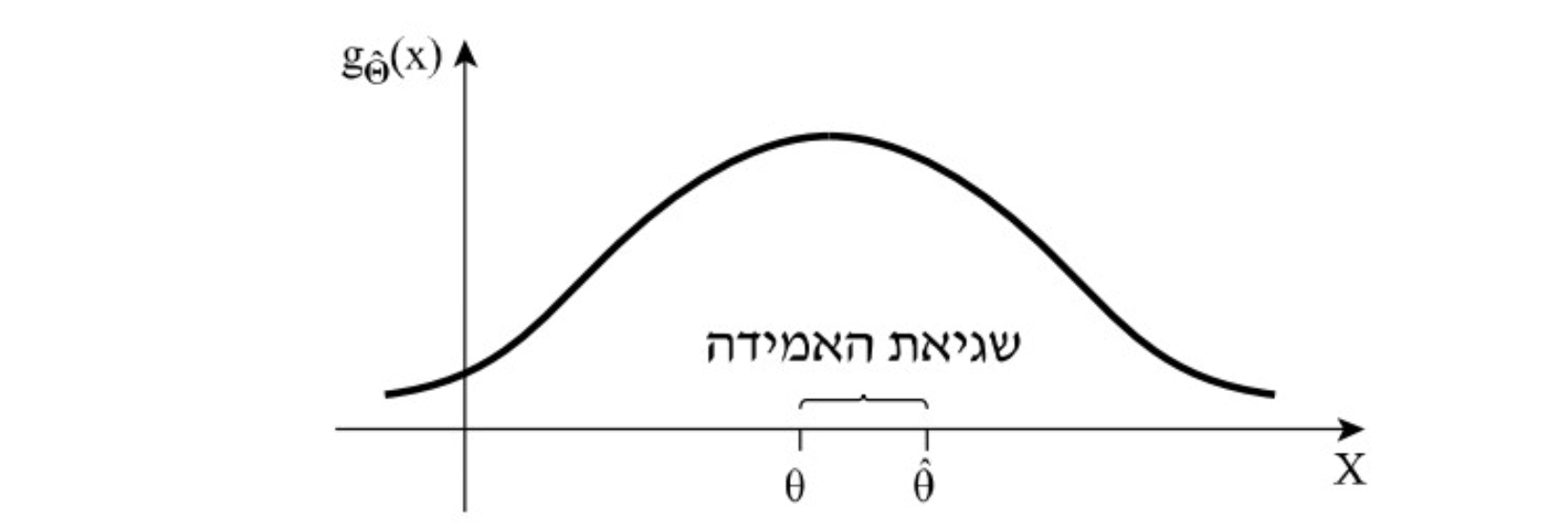
כלומר, מתוך אוכלוסייה בעלת הפרמטר
שגיאת אמידה:
כיוון שאומד הוא משתנה מקרי והוא מקבל ערכים שונים אז ברור שבניסויי דגימה שונים נוכל לקבל ערכים שונים לאומד. נגדיר שגיאת אמידה להיות
תכונות האמד
א. עקביות- ככל שהמדגם גדול יותר ההסתברות שהאמד יתכנס לפרמטר האמיתי
ב. אי הטיה- התוחלת של האמד שווה לפרמטר
נשים לב אלו תכונות לקביעה של אמד תקין, הם לא חייבים בהכרח להתקיים.
אומד חסר-הטיה
ננסה לענות על השאלה: כיצד נבחר איזה סטטיסטי יש לחשב במדגם שנוציא, כדי לאמוד את הפרמטר בצורה הטובה ביותר.
אנחנו מחפשים סטטיסטי שיקיים
כלומר, נחפש סטטיסטי כזה שאילו היינו מוציאים אינסוף מדגמים בגודל שהחלטנו עליו, ובכל מדגם היינו מחשבים את הסטטיסטי שבחרנו, אז ממוצע ההתפלגות של כל הערכים הללו הייתה שווה בידיוק לפרמטר.
סטטיסטי
אומד ייקרא מוטה אם השיוויון אינו מתקיים.
אם כן, ממוצע המדגם הוא דוגמה לאומד חסר הטיה עבור הפרמטר התוחלת.
שכן התוחלת שלו שווה בידיוק לתוחלת של הפרמטר.
במצב שבו
כלומר התוחלת של שגיאת האמידה היא
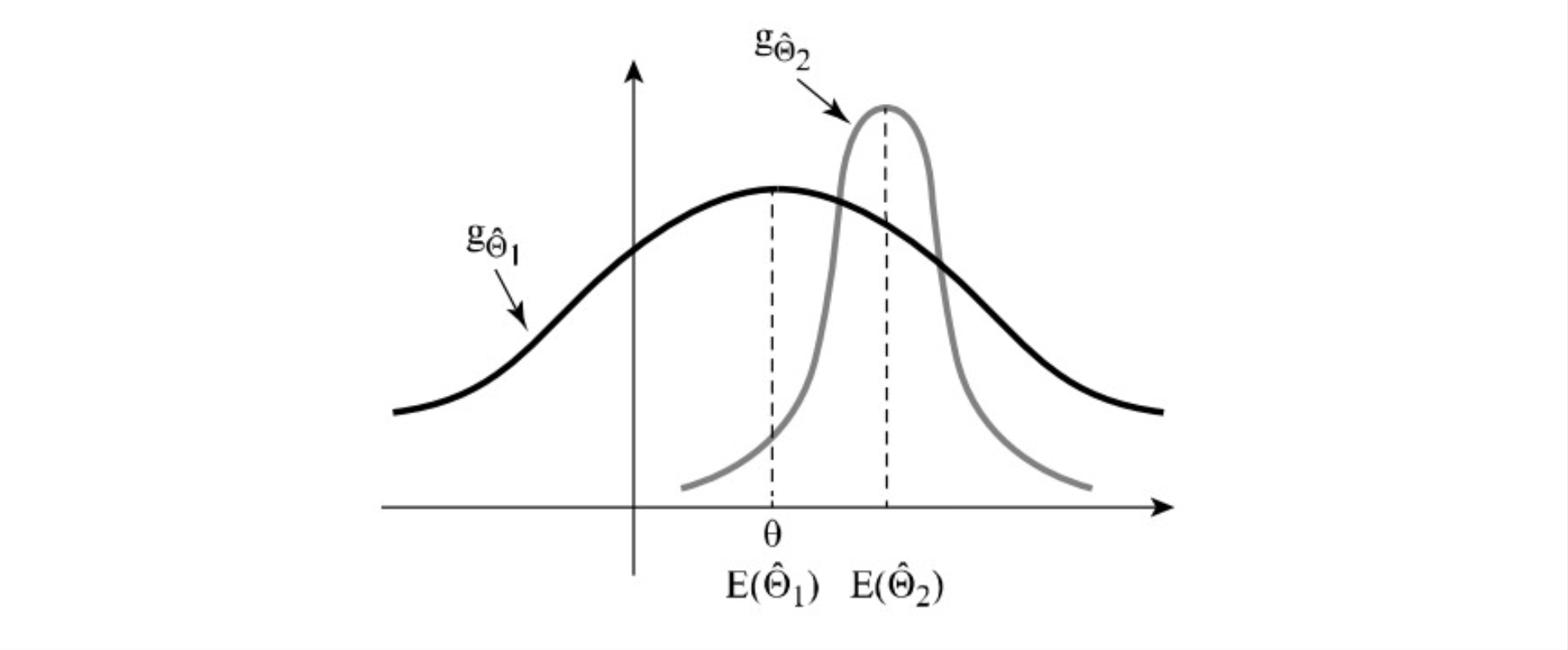
למשל , ההתפלגות הראשונה היא חסרת הטייה ביחס ל
אומדים חסרי הטיה לתוחלת ושונות
ממוצע המדגם
הראנו כבר שממוצע המדגם , ללא תלות בגודלו וללא תלות בהתפלגות של
כפי שכבר אמרנו, המתבקש מכך הוא שממוצע המדגם הוא אומר חסר הטיה לתוחלת
אומד לשונות
ננסה לבנות אומד חסר הטיה לשונות
זה מאוד דומה לשונות המדגם אם כי ההבדל הוא שכאן מודדים את המרחק מהתוחלת ולא ממוצע המדגם.
נוכיח שזהו אומד חסר הטייה על ידי חישוב תוחלתו
לפי ההגדרה של מדגם מקרי, לכל
ולכן הנ״ל הוא אומד חסר הטייה לשונות.
החסרון העיקרי של אומד זה הוא התלות בתוחלת שהרבה פעמים לא ידועה לנו, לכן הפתרון הטבעי ביותר העולה על הדעת הוא להחליף את התוחלת באומד שלו
באופן הזה התוחלת תהיה
נסמן את הביטוי הנ״ל
ביטוי השונות עד כה:
א. השונות באוכלוסייה או במ״מ (בהתפלגות הסתברותיות) היא
ב. השונו במדגם מסוים (בהתפלגות שכיחויות) היא
בשני המקרים השונות היא מדד פיזור, המבוטא על ידי ממוצע ריבועי הסטיות מן הממוצע של האוכלוסייה או המדגם
ג. אומד חסר הטיה לשונות של האוכלוסייה על סמך מדגם
ד. במדגם מסוים נקבל את הערך
קיים כמובן קשר בין
כלומר נוכל לקחת את האומדן לשונות של האוכלוסייה ולתאר איתו את מידת הפיזור של הסטטיסטי בתוך המדגם.
המסקנה : ככל שהמדגם גדול יותר כך ההבדל בין האומדן לבין שונות המדגם קטנה יותר ולכן שונות המדגם מהווה אומד כמעט חסר הטיה ל
שיטות אמידה
שיטת המומנטים
שיטת המומנטים היא שיטת אמידה לפרמטרים שמאפיינים התפלגות של אוכלוסייה מסויימת.
נגדיר את המומנט ה
נניח שיש לנו התפלגות עם פרמטרים לא ידועים
בהינתן המדגם בגודל
בעצם הרעיון הוא:
- נשווה כל מומנט מסדר
לאומדן שלו במדגם. - נפתור מערכת של
משוואות עם נעלמים עבור האומדנים כדי לקבל אומדן עבור כל פרמטר באוכלוסייה.
חשוב לשים לב שאנחנו עושים את זה עבור מדגם בודד מגודל כלשהו.
למה מומנטים?
- מומנט מסדר ראשון זוהי התוחלת: מדד למרכז ההתפלגות.
- מומנט מסדר שני מבטא שונות: מדד לפיזור סביב תוחלת ההתפלגות.
- מומנט מסדר שלישי מבטא skewness: מדד לסמטריה סביב התוחלת.
- מומנט מסדר רביעי מבטא kortosis: מדד מקובל למידת הריכוז של פונקציית צפיפות או התפלגות של משתנה מקרי ממשי.
המומנטים בעצם נותנים לנו את מידע על ההתפלגות כפי שהיינו יכולים להניח אם היה לנו את פונקציית ההסתברות מצויירת.

השיטה פשוטה וקלה לחישוב, אך יכולה לפעמים לתת אומדנים מוטים. בדרך כלל עדיף את שיטת הנראות המירבית עליה נדבר בהמשך.
נסתכל על הדוגמה הבאה
נרצה למצוא אומד לפי שיטת המומנטים ל
כעת זהו ממוצע המדגם
נוכל אם כן להסיק ש
דוגמה 2:
בכד 100 כדורים וידוע ש
נדגמו
ההסתברות להוציא בצבע כדור כחול היא
מספר הכדורים בצבע כחול
התוחלת של משתנה בינומי היא
כלומר המומנט הראשון שהוא התוחלת יקיים שערכו הוא
ממוצע הכדורים הכחולים במדגם שלנו הוא
כעת, חזרו על הניסוי פעמיים נוספות והפעם התקבלו
מליניאריות התוחלת נקבל
סכום של בינומי מתפלג בינומי
דוגמה 3:
נסתכל על התפלגות מעריכית
התוחלת שהיא המומנט מסדר ראשון שווה ל
כעת נבצע מדגם
האומד לתוחלת על סמך המדגם יהיה
דוגמה 4:
נסתכל על התפלגות אחידה
התוחלת היא
נשים לב להטייה שיכולה לקרות לנו כאן, אם
מצב שבו יש לנו שתי נעלמים:
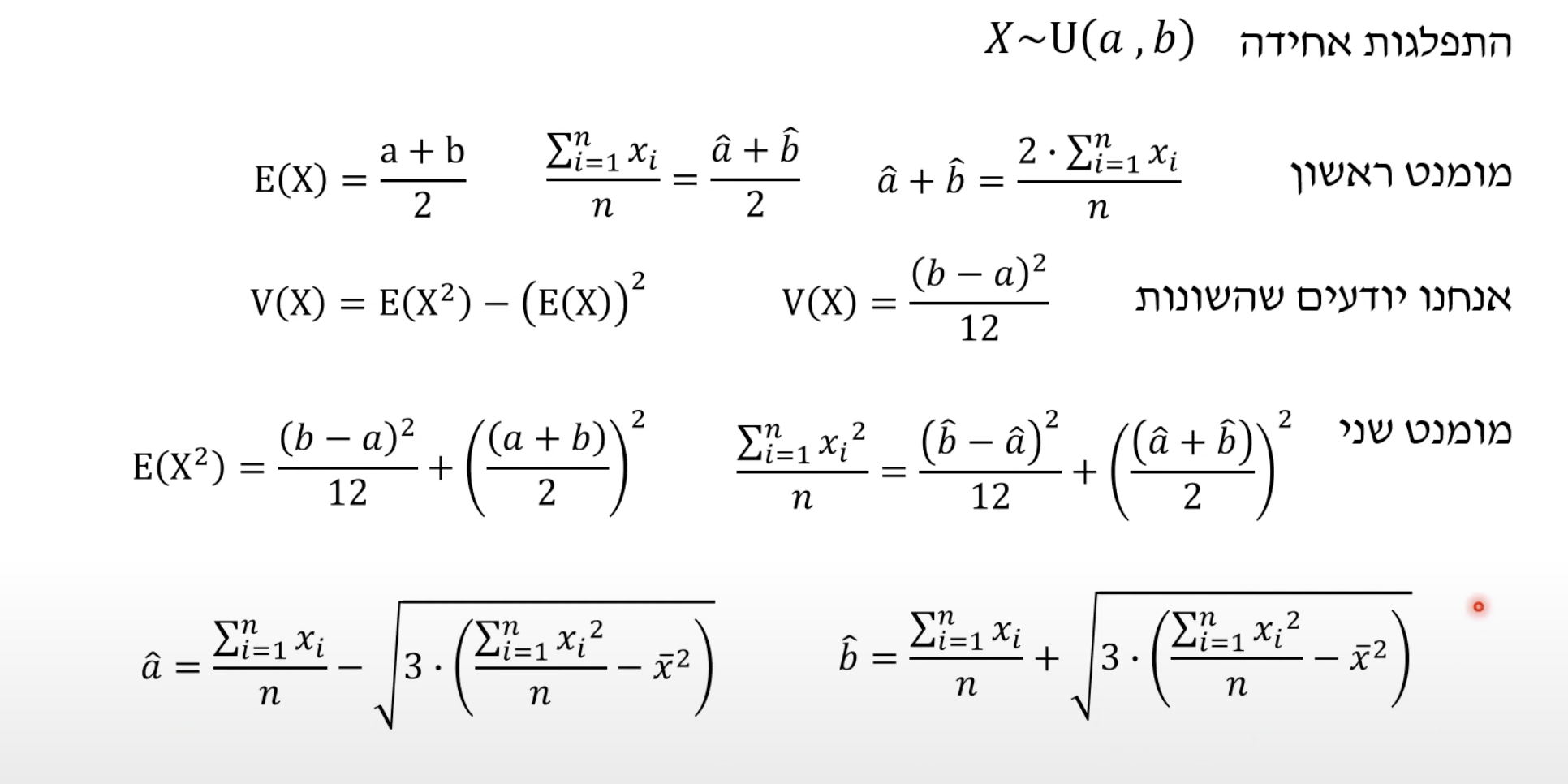
אמד נראות מקסימלית
בהינתן פרמטר לא ידוע
נבצע מדגם בגודל
אומד נראות מקסימלית
פונקציית הנראות תהיה
נמצא את הערף
כדי לקבל את הערך המקסימלי נוכל לגזור ולהשוות ל
באופן אינטואיטיבי הגישה אומרת שכדי לנבא היטב את הפרמטר האמיתי על-סמך מדגם מקרי מסוים, יש לבדוק איזה פרמטר מתוך כל האפשרויות הוא זה ש"יסביר" בצורה הטובה ביותר את המדגם. כלומר אומד הנראות המרבית הוא הפרמטר שאילו היינו מציבים בפונקציית ההתפלגות מראש, הוא היה נותן את ההסתברות הגבוהה ביותר לקבל את המדגם שאכן התקבל
דוגמה 1:
ישנם 3 כדים עם כדורים כחולים וסגולים.
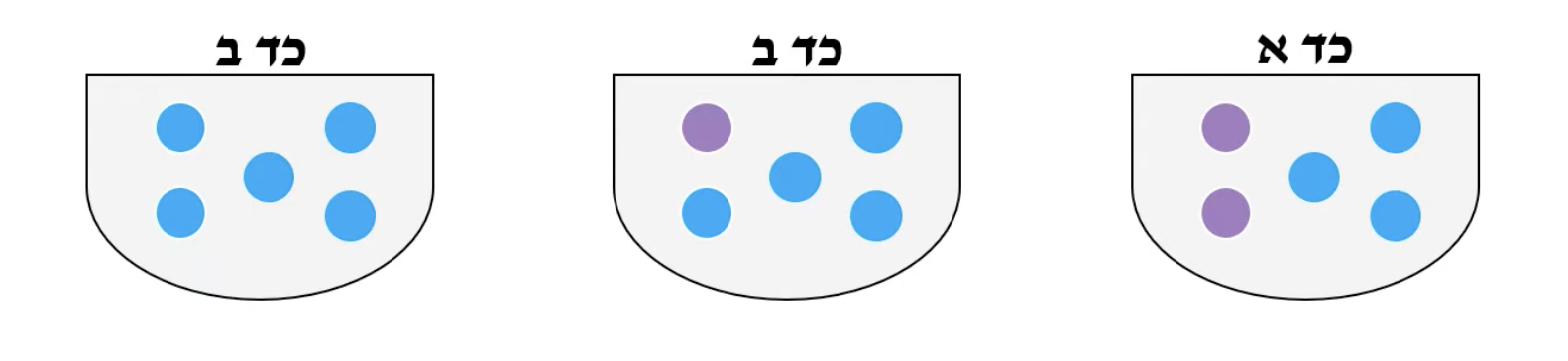
בחרנו באופן מקרי כד והוצאנו ממנו 3 כדורים ללא החזרה, בנה אומדן נראות מקסימלית לכד הנבחר, אם הכדור הראשון ושני יצאו כחולים, והשלישי סגול.
נחשב את ההסתברות לקבל את התוצאה הרצויה בכל כד:
כד א:
כד ב:
כד ג:
בעצם נרצה את ההסתברות המקסימלית מבין הכדים שזה אומר ש אנ״מ - כד א׳ או כד ב׳.
כאשר אין תלות באיזשהו פרמטר פשוט ניקח את ההסתברות המקסימלית בהתפלגות.
דוגמה 2:
מספרי קלפי
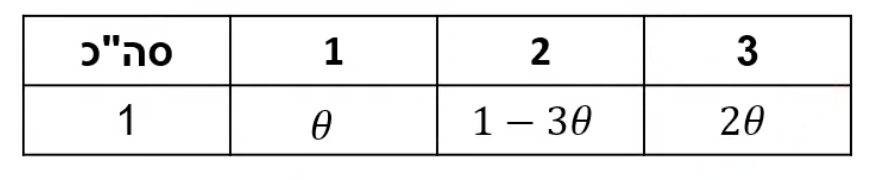
המספר קלפים יכול להיות
נרצה למצוא אומדן נראות מקסימלית ל
נרשום את פונקציית הנראות
נגזור ונשווה ל
כמובן ש
ולכן זאת נקודת מקסימום.
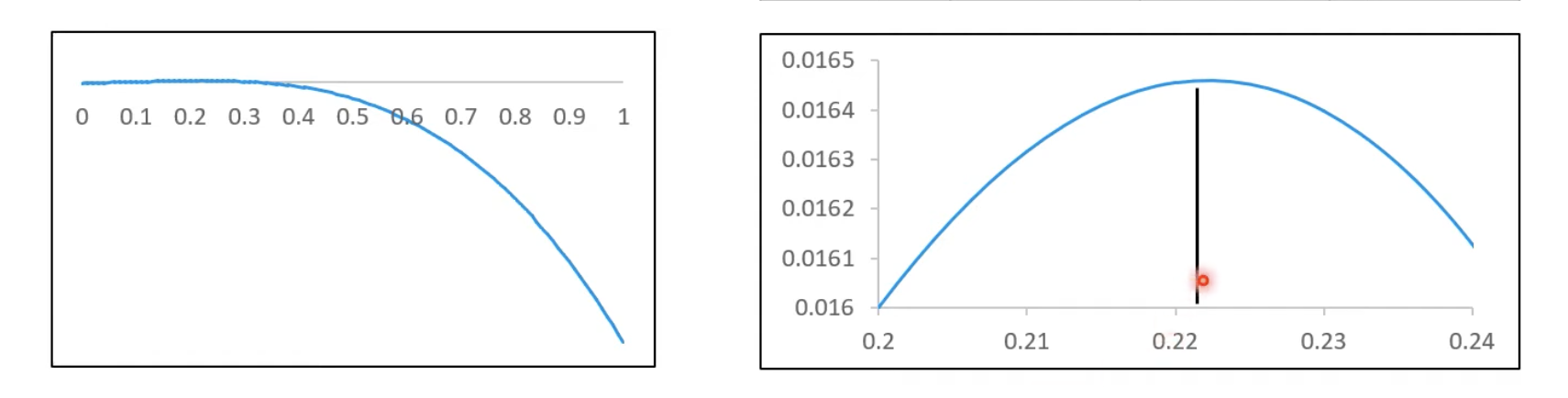
אם
למשל, אם נרצה את אומדן נראות מקסימלית לקבל 3 קלפים. כלומר ל
מהתכונה הנ״ל אנחנו יודעים ש
דוגמה 3:
נתונה פונקציית הצפיפות הבאה, מצא אנ״מ על סמך 10 תצפיות ב״ת
המכפלה תהיה
מתקיים שככל שערכה של
דוגמה 4:
זמן ההמתנה בדקות לנציג מתפלג מעריכית עם פרמטר
נצטרף גם
פונקציית המכפלה תהיה
למקסם פונקציה שקול ללמקסם את הln ולכן :
מכאן כבר לא בעיה לגזור...
דוגמה 5:
נניח הטלת מטבע מזויף אשר בו בהסתברות
מה ההסתברות לקבל
התפלגות הטלת המטבע היא בינומית
לרוב היינו רוצים לחשב את ההסתברות ולכן הנעלם היה
גם כאן נוכל להשתמש בפונקציית ה
לסיכום:
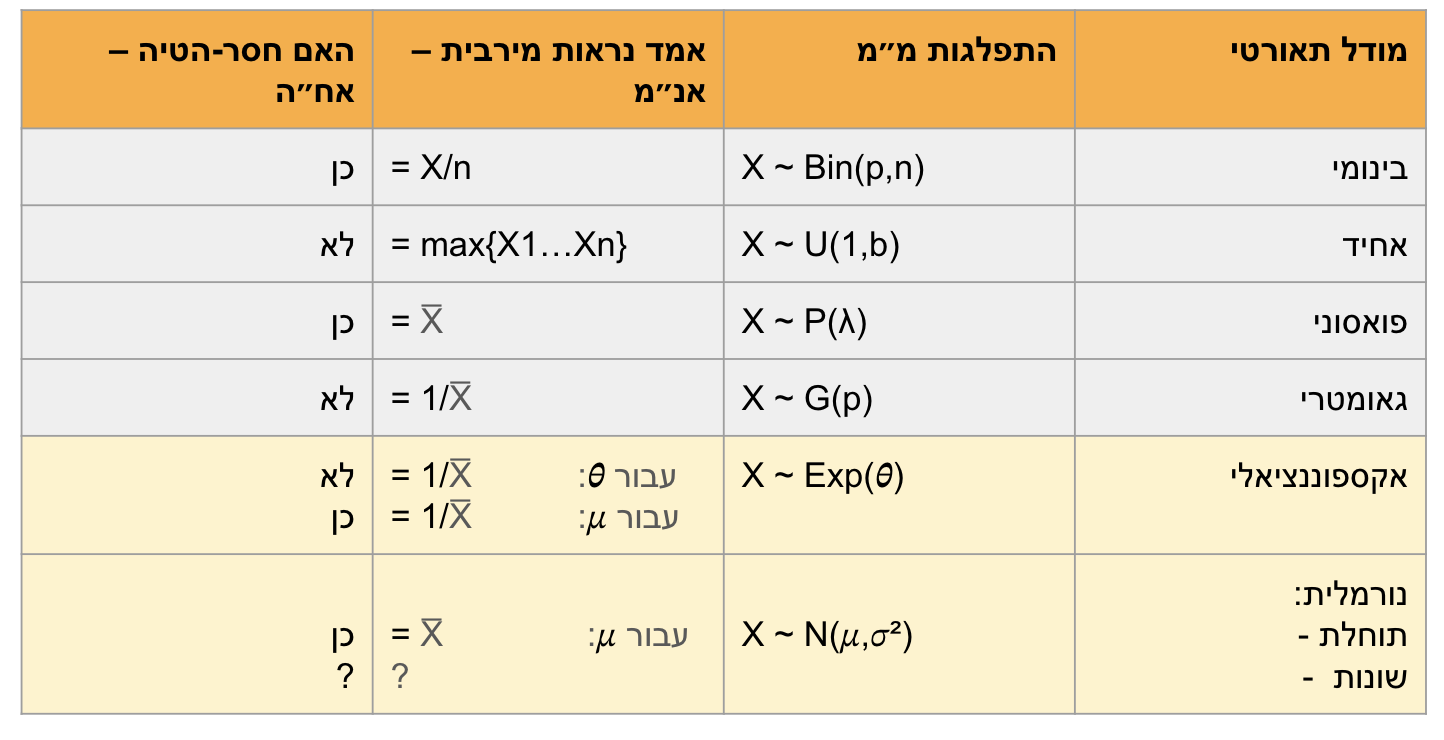
משפט:
האנ״מ לתוחלת יהיה ממוצע המדגם.
האנ״מ לשונות תהיה השונות במדגם הוא מעט מוטה כפי שכבר הראנו והוא לא האומדן חסר הטייה שבו מחלקים ב
יעילות של אמדים
כאשר יש לי
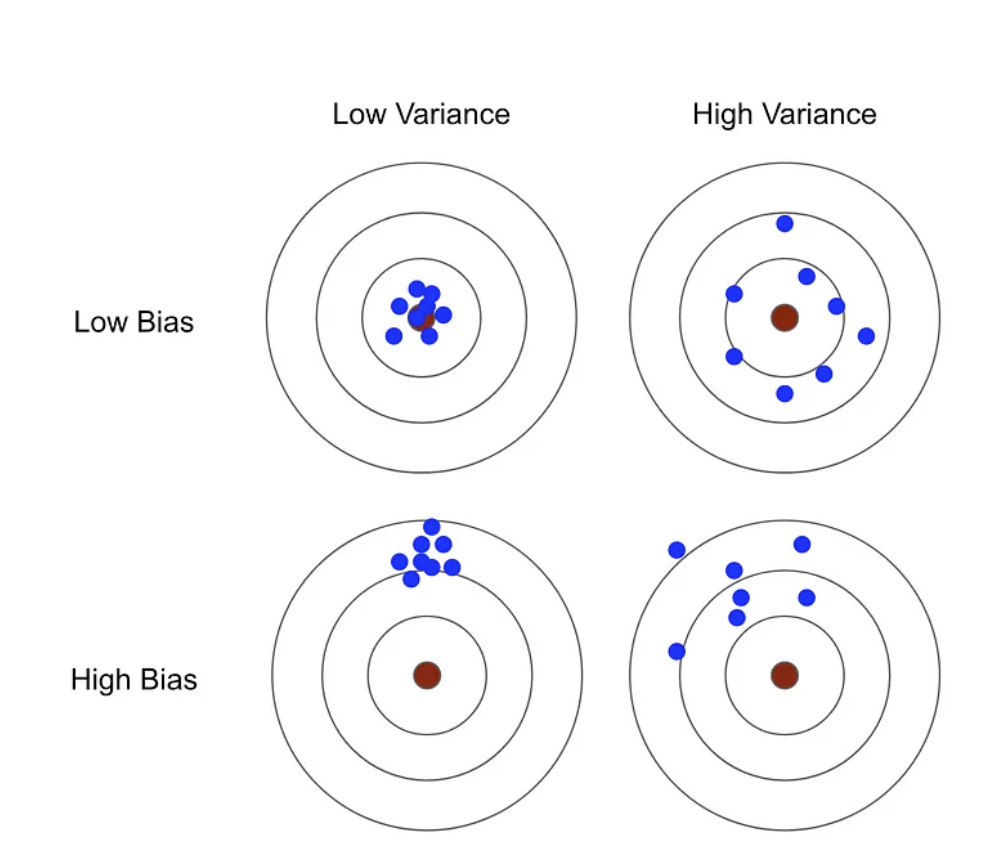
MSE
במקרה הכללי של הנ״ל במצב שבוא האמדים אינם חסרי הטיה, נרצה לחשב את
אמידה סטטיסטית עבור קשר בין 2 משתנים
נניח שיש לנו שני משתנים מקריים
נשאלת השאלה איך בוחרים קו מגמה?
נזכיר שקו מגמה הוא האומד את הקשר בין שני המשתנים האלה למרות שלפי מקדם המתאם של פירסון יש בינהם קשר ליניארי שאינו חזק בהכרח.
האינטואיצייה תהיה לבחור גרף ישר שהכי קרוב לנקודות בדיאגרמה לשם כך נשתמש ב אמד ריבועים פחותים. בעצם אנחנו רוצים לאמוד את הקשר הליניארי הנ״ל
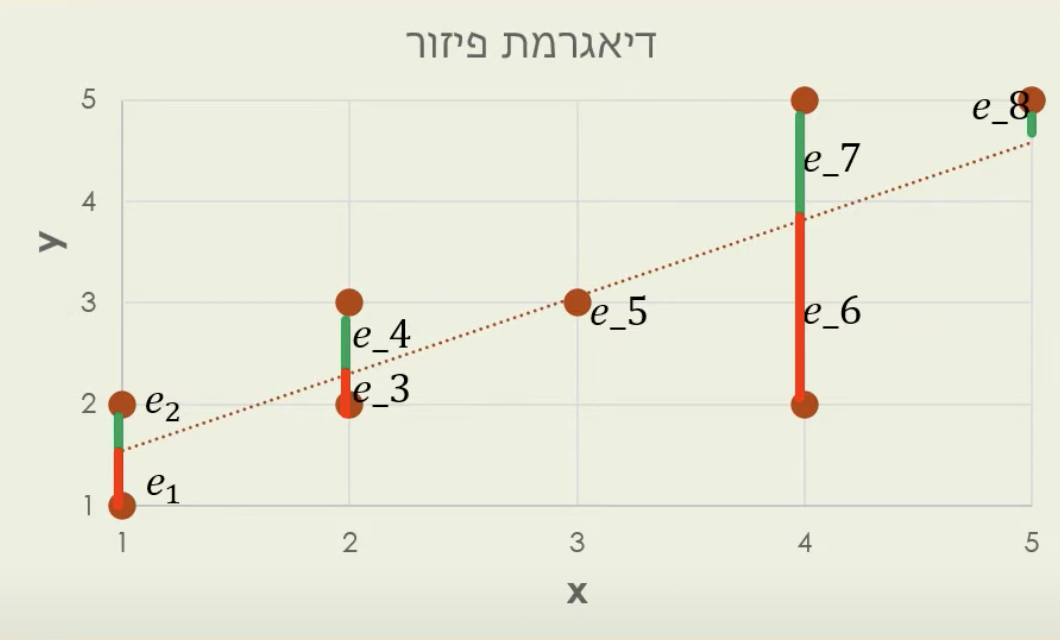
אם כן, העקרון הריבועים הפחותים מבקש שנבחר את הישר שיקיים :
א.
ב.
כדי לחשב את הקו השיקיים את הנ״ל:
שיפוע הקו:
החותך:
נוכל לחשב גם בדרך נוספת:
כלומר מקדם המתאם כפול סטיית התקן של
דרך נוספת:
וגם
טיב הקו, איכות ההסבר:
ברגרסיה אנחנו מדברים על להסביר את
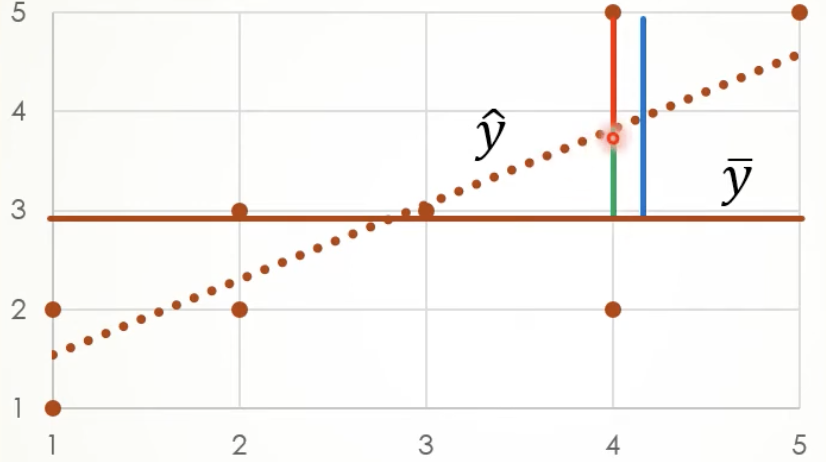
כדי להסביר נרצה לחשב את אורך הכו הכחול. שבודק את השונות של ערך האומדן
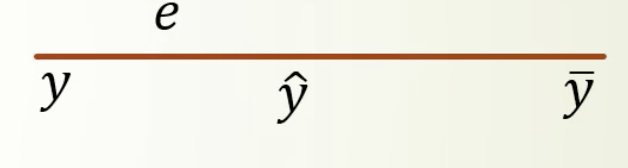
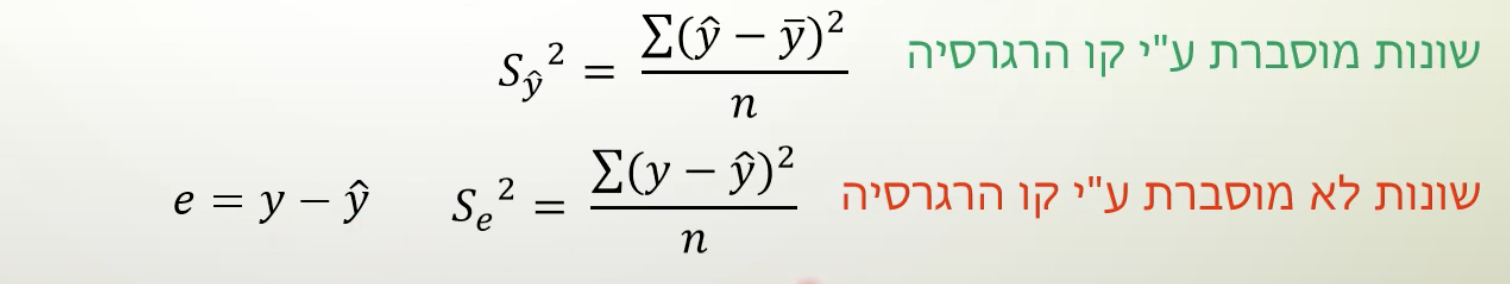
כעת נגדיר את אחוז השונות המוסברת להיות על ידי
לא אוכיח את המעבר האחרון