דיברנו על אומדן סטטיסטי נקודתי לפרמטר ועל אומדנים המקיימים תכונות מסויימות כמו חוסר הטייה.
נרצה כעת לענות על השאלה מהי מידת הדיוק של האומד.
כפי שניתן לצפות, מידת הדיוק של אומד תגדל ככל שהמדגם שעליו הוא מבוסס גדול יותר.
מכאן תעלה באופן טבעי שאלה נוספת: מה צריך להיות גודלו של המדגם שיבטיח רמת דיוק רצויה באמידה מסוימת?
מידת הדיוק של אומד
משפט הגבול המרכזי שבמדגם מקרי מתוך משתנה מקרי בעל תוחלת ושונות מתקיים עבור
כלומר עבור מדגמים גדולים מ ממוצע המדגם מתפלג נורמלית (בקירוב). ואם המ״מ שממנו דוגמים מתפלג נורמלית אז בלי תלות ב ממוצע המדגם גם מתפלג נורמלית.
נסתכל על הדוגמה הבאה:
במדגם שגודלו מתוך מ״מ המפולג נורמלית בעל סטיית של ותוחלת נרצה לדעת מהי ההסתברות שממוצע המדגם שיתקבל יהיה שונה מ בלא יותר מ יחידות.
כלומר נתון לנו ו מכאן שממוצע המדגם מפולג נורמלי עם תוחלת ושונות (כלומר סטיית תקן ). .
אנחנו מנסים לחשב את ההסתברות . ננרמל כל אחד מהטווחים: , כלומר לאחר הנרמול מתקיים .
השאלה ״מהי ההסתברות שהממוצע יהיה במרחק 4 יחידות מממוצע ההתפלגות״ שקולה לשאלה ״מהי ההסתברות שהממוצע יהיה במרחק 2 סטיות תקן מממוצע ההתפלגות״. זאת משום שסטיית התקן של ההתפלגות היא . נחשב ונקבל
התרשים מציג את התוצאה שקיבלנו כאשר ציר הוא ציר שאומד את המרחק ביחידות של סטיות תקן.
אפשר להתסכל על זה גם בדרך אחרת:
הציר האנכי הוא ציר , כלומר ערכי המשתנה . על הציר האופקי מסומנים מספרי הניסויים (החזרות על הדגימה). כל נקודה מתארת ערך של ממוצע המדגם עבור הניסוי ה בציר האנכי. ככל שנעשה יותר דגימות נראה כי מהערכים נמצאים בסביבה של יחידות סביב התוחלת.
האי שיוויון:
שקול לאי שיוויון
ולכן גם ההסתברות . נבטא זאת באופן מילולי: הוא רווח-סמך ברמה של עבור . כלומר, במדגם שגודלו מתוך מ״מ המפולג נורמלית עם סטיית תקן ותוחלת בלתי ידועה, ההסתברות ש תהיה שונה ממוצע המדגם בלא יור מאשר יחידות היא .
נדגיש כי הוא קבוע ובלתי ידוע ואילו קצוות הטווח משתנים מניסוי לניסוי.
ניתן לראות בתרשים את רווח הסמך הנ״ל כל נקודה מותחת קו של 4 יחידות מלמעלה ומלמטה וניתן לראות שכ מהנקודות אכן חוצות את הקו האופקי שמתאר את .
השיוויון הוא מקרה פרטי של שיוויון מהצורה כאשר הוא הפרמטר הנאמד.
הרווח נקבע על ידי הסטטיסטי האומד ומשתנה ממדגם למדגם (נקרא ״רווח מקרי״). הוא קריטריון דיוק שבדרך כלל יהיה קרוב ל. כלומר הרווח הוא רווח-סמך ברמה של אחוז עבור .
באופן כללי אפשר לבטא את רווח הסמך מהדוגמה שלנו כך
כדי שאגף ימין ישווה ל צריך שיתקיים . נסמן את ערך המקיים זאת כ ונציב:
כל שנשאר לעשות כעת הוא להחליף בסדר של הא״ש ונקבל
כלומר רווח-סמך ברמה של אחוז עבור הוא
מסקנה
ככל שרמת הסמך גבוהה יותר, כך מתרחב רווח הסמך
הקשר בין גודל המדגם לדיוק הנדרש
במקרים רבים אנו קובעים מראש את רמת הסמך באחוזים ושואלים מהו גודל המדגם, שיבטיח ברמת סמך זו, ששגיאת האמידה, כלומר ריחוקו של האומד מן הערך האמיתי , לא תעלה על . במילים אחרות, נרצה להבטיח שנקבל רווח סמך של ברמת סמך . כלומר נרצה לפתור את הביטוי
סך הכל נקבל
וכדי להבטיח ש נחליף את הכמת בכמת . וסך הכל קיבלנו ביטוח לגודל המדגם.
עקרונות של בדיקת השערות
האומדן של פרמטר בלתי ידוע הוא רק יישום אחד של ההסקה הסטטיסטית.
לעתים קרובות יותר משאנו מעוניינים באומדן של פרמטר, אנו מעוניינים בבדיקת השערה מסוימת שיש לנו לגביו.
נסתכל על דוגמה של מבחן סטטיסטי כדי להבין יותר טוב:
אל משרד המסחר והתעשייה הגיעו תלונות צרכנים על כך, שמשקל הלחם הנאפה במאפייה מסוימת נופל מן המשקל הנקוב על האריזה שהוא 500 גרם.
כדי לבדוק את התלונה הזו, החליט המשרד לבצע מבחן סטטיסטי כלומר בדיקת השערה בשיטות סטטיסטיות. לשם כך נדגמו ונשקלו 30 כיכרות לחם של אותה מאפייה והרי המשקלים:
אנשי המחקר במשרד מודעים לכך שלא ייתכן שמשקלה של כל כיכר יהיה בידיוק 500 גרם. הניסיון הראה כי סטיית התקן של משקלן של כיכרות לחם הנאפים במאפייה מודרנית, תוך הקפדה סבירה על אחידותן, היא 3 גרמים, אך תוחלת המשקל חייבת להיות 500 גרם.
אנשי המחקר צריכים להסיק מתוך הנתונים שנאספו במדגם של 30 ככרות הלחם אם הצרכנים צדקו בתלונתם.
נמצא שממוצע המשקלים של כיכרות הלחם במדגם הוא גרם. משקלה של כיכר לחם הוא משתנה מקרי, שיכול לקבל ערכים שונים, וכך גם ממוצע המדגם . לכן, גם כאשר תוחלת המשקל של כיכרות הלחם היא ממוצע המשקלים של מדגם מקרי בן יכול להיות שונה. אולם, ממוצע כזה יכול גם לרמז שתוחלת המשקל אינה גרם אלא פחות מכך. התוחלת, אם כן, ״עומדת למשפט״ ואנשי המחקר משערים שתי השערות מנוגדות עליה:
תוחלת המשקל שווה ל 500 ורק במקרה התקבל במדגם ממוצע שונה.
התוחלת של המשקל קטנה מ500 וממוצע המדגם מרמז על כך.
החוקרים כעת צריכים להחליט באיזו משתי ההשערות לתמוך לאור המדגם הנתון, שהממוצע שלו הוא .
הגישה שהחוקרים נוקטים היא: נניח שההשערה הראשונה נכונה, כלומר תוחלת המשקל של כיכר לחם היא אמנם 500 גרם. באיזו מידה סביר לקבל מדגם שהממוצע שלו זהה לממוצע שנתקבל או קטן ממנו?
כלומר, החוקרים רוצים לבדוק , בהנחה שטענת המאפייה נכונה. אם יתברר שהסתברות זו קטנה מאוד, החוקרים ייאלצו להסיק שתוחלת המשקל של כיכר לחם במאפייה זו כנראה קטנה מ ושהמאפייה פוגעת בציבור הצרכנים. אבל אם יתברר שבמדגם בגודל ״סביר מאוד״ לקבל ממוצע כנ״ל או קטן ממנו (מתוף מ״מ עם תוחלת גרם וסטיית תקן של גרם), אזי אין לבוא בטענות אל המאפייה.
על מנת לבדוק את ההסתברות הנ״ל החוקרים נעזרים בעובדה שהמדגם בגודל 30 ומניחים ש
במקרה שלנו ו השונות היא . כלומר .
כעת אפשר לחשב את ההסתברות באמצעות נרמול.
למרות שחישבנו את ההסתברות, החוקים עדיין לא יודעים מה זה אומר הסתברות ״קטנה״ או ״סבירה״ לכן צריך להחליט לפני שמחשבים את ההסתברות , כלל הכרעה ומחליטים לפיו. למשל, אם יוברר שההסתברות שיתקבל ממוצע של ומטה היא או פחות תחת התפלגות הדגימה הנ״ל, הרי ההשערה המצדיקה את המאפייה תידחה, וההשערה המצדיקה את הצרכנים תתקבל.
עוד לפני חישוב ההסתברות, ניתן לראות שהחוקרים קובעים לעצמם איזשהו כלל הכרעה ולמעשה קובעים את הגבול בין הסתברות ״ניכרת״ להסתברות ״זעומה״. בהתאם לכך, יכולים החוקרים לבדוק באיזו השערה לתמוך לפי כלל ההכרעה שקבענו.
זוהי התפלגות הדגימה הנורמלית שתיארנו למעלה.
אם ננרמל את ההתפלגות שלנו נקבל , אנו יודעים שבהתפלגות זו הערך שמתחתיו נמצאים אחוז מן ההתפלגות הוא : הוא: .
לפיכך נוכל להציע את הכלל הבא:
אם ציון התקן של ממוצע המדגם קטן מ נקבע שתלונת הצרכנים מוצדקת.
במילים אחרות: אם בגרף הנ״ל יימצא שערך המשתנה המתאים לממוצע המדגם הוא משמאל לנקודה אז נקבל את טענת הצרכנים אחרת נקבל את טענת המאפייה.
לאזור משמאל קוראים אזור דחייה ולתחום מימין קוראים אזור קבלה. אם נחשב נראה שציון התקן ולכן על החוקרים להסיק כי מאחר שההסתברות לקבל את הערך או ערך נמוך ממנו, ממשתנה מקרי שתוחלתו גרם (עם ) היא קטנה, יש יסוד לחשד שתוחלת המשתנה המקרי אינה גרם אלא קטנה יותר, ויש לדחות את טענ המאפייה, כלומר לקבל את טענת הצרכנים.
באופן שקול, יכולים החוקרים לקבוע רווח סמך ל לפי ממוצע המדגם ברמה של .
הנוסחה הכללי של רווח סמך היא
אם רמת הסמך היא אז ו כלומר כלומר :
אם כן, נוכל להציב בנוסחה הנ״ל את
כאשר נציב נקבל
You can't use 'macro parameter character #' in math mode497.42<\mu< 499.58$$ נזכיר שהמשמעות של רווח סמך היא שאם היינו מוציאים אינסוף מדגמים בגודל $30$ מאותה אוכלוסייה ועבור כל אחד מהם מחשבים ממוצע ורווח סמך, היינו מקבלין ש$95$ אחוז מהרווחים היו כוללים את הפרמטר ו $5\%$ לא היו כוללים אותו. לפי הרווח סמך קיבלנו שהתוחלת $500$ לא נמצאת בתחום ברווח הסמך שרצינו ולכן גם כאן יש תמיכה בצרכנים שהתוחלת איננה 500 גרם. >[!note] הבחנה >אם יש לנו השערה כלשהי $H_{0}$ נרצה לבדוק האם בהנחה שהיא נכונה ממוצע המדגם שלנו נמצא באזור הדחייה או לא. באופן מקוצר לדרך הנ״ל אפשר לחשב את אזור הדחייה נסמנו $C$ על ידי $$C=\mu + z_{1- \frac{\alpha}{2}} \frac{\sigma}{\sqrt{n}}$$ בעצם זה שקול לחישוב שעשינו למעלה שבוא קבענו מהו אזור הדחייה לפי רמת המובהקות ($\alpha$) רק שבמקום להתאים את המדגם להתפלגות נורמלית סטנדרטית מבצעים התאמה של אזור הדחייה להתפלגות של ממוצע המדגם $\overline{X}\sim N(\mu,\frac{\sigma^{2}}{n})$ . לאחר מכן כל שצריך לעשות הוא האם ממוצע המדגם הספציפי שלנו נמצא בטווח המתאים לפי ההשערה $H_{1}$ . ### שלבים כלליים לבדיקת השערות #### קביעת ההשערות בכל בדיקת השערות מנוסחות שתי השערות אשר סותרות זו את זו. __השערת האפס__ : $H_{0}$ - מתארת את ההנחות הקיימות בנקודת מוצא. __השערה אלטרנטיבית__ : $H_{1}$ 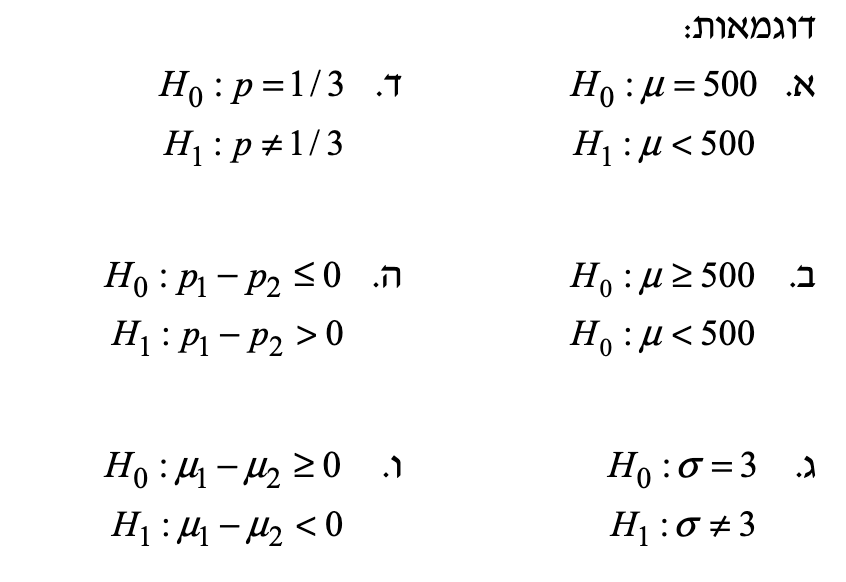 הדוגמאות מדגימות מספר מצבים: 1. ההשערות יכולות להתייחס לפרמטרים שונים. 2. השעה יכולה להתייחס לפרמטר של אוכלוסייה אחת או להשוואה של פרמטר מסויים באוכלוסיות שונות. 3. בהשערות לגבי פרמטר של אוכלוסייה, או של משתנה מקרי, נהוג להבחין בין __השערה פשוטה-__ שבה ערכו של הפרמטר נקוב בה באופן חד משמעי. __השערה מורכבת-__ שבה מצויין טווח שבו נמצא הפרמטר. 4. ההשערות ייקראו __חד צדדיות__ אם $H_{1}$ מתייחס רק לערכים שנמצאים מצד אחד לערך הנקוב ב$H_{0}$ ו __דו צדדית__ כאשר $H_{1}$ מתייחס לערכים הנקובים משני הצדדים. האפשריות הנ״ל משפיעות על קביעת אזור הדחייה שלנו. 1. בדוגמה הנ״ל אזור הדחייה היה רק בצד שמאל של ההתפלגות כיוון שההשערה האלטרנטיבית הייתה $\mu<500$ . 2. אם ההשערה האלטרנטיבית הייתה $H_{0}:\mu=500$ כלומר $H_{1}:\mu\neq 500$ כלומר השערה דו״צ אז אזור הדחייה היה מחולק לפי כלל ההכרעה לשני חלקים (במקרה של הדוגמה 5%) אזור המתאים ל 2.5% מימין ואזור מתאים ל 2.5% משמאל. __לסיכום__ בקביעת ההשערות אנחנו בפועל מתייחסים ל3 אפשריות: א. $H_0:\theta=c,H_{1}:\theta>c$ ב. $H_0:\theta=c,H_{1}:\theta<c$ ג. $H_0:\theta=c,H_{1}:\theta\neq c$ #### בחירת סטטיסטי לאחר שנוסחו ההשערות, יש לבחור בסטטיסטי שיהווה אומד מתאים לפרמטר שנבדק ושאותו נחשב מהמדגם. בדרך כלל נשתמש בסטטיסטי המהווים __אומד חסר הטייה. #### קביעת ההנחות קביעה של הגבול בין אזור הדחייה לאזור הקבלה. בשביל זה צריך לדעת את התפלגו הדגימה של המ״מ בו נשתמש, כדי להכריע בין $H_{0}$ ל $H_{1}$ . הרבה פעמים התצפיות מפולגות בהתפלגות נורמלית או בינומית. אם אנחנו לא יודעים את ההתפלגות של תצפיות אז הבעיה נעשית סבוכה יותר. #### קביעת גודל המדגם ממשפט הגבול המרכזי אנחנו יודעים של $n$ יש חשיבות גבוהה בקביעת התפלגות הדגימה. וגם תהיה לו חשיבות בחישוב הסתברות ההכרעה המוטעית. #### חישוב התפלגות הדגימה כל מה שהגדרנו למעלה, מאפשר את חישוב של התפלגות הדגימה כדי לבדוק מהי ההסתברות לקבלת ערך הסטטיסטי שנתקבל במדגם בהנחת נכונות $H_{0}$ . #### קביעת רמת המובהקות קביעת כלל ההכרעה, שבו יהיה תלוי גודל אזור הדחייה. אחוז זה מסומן ב$\alpha$ ונקרא __רמת המובהקות__ של מבחן. בעצם זהו גודל השטח של אזור הדחייה של $H_{0}$ בהתפלגות הדגימה, בהנחה ש $H_{0}$ נכונה. זה גם מסמן את ההסתברות שקיבלנו מדגם יוצא דופן אשר יטעה אותנו ונדחה את $H_{0}$ למרות שהיא נכונה. #### קביעת אזורי דחייה וקבלה אזורי דחייה וקבלה של ההשערה $H_{0}$. גודל האזור נקבע לפי רמת המובהקות, ומיקומו בהתפלגות הדגימה תלוי בסוג ההשערה: חד צדדית או דו צדדית.