מודלים הסתברותיים

המודל ההסתברותי הוא תיאור מתמטי של מצב לא ידוע. עליו להיות מתואר עם מסגרת בסיסית והוא מכיל שתי מרכיבים עיקריים.

1. מרחב המדגם : $\mathrm{\Omega }$, קבוצה שמתארת את כל התוצאות האפשרויות של הניסוי.
2. חוק הסתברות : חוק זה מוקצה לקבוצה $A\subseteq \mathrm{\Omega }$ של תוצאות אפשרויות ($A$ נקרא גם מאורע) מספר אי-שלילי שמסומן $P(A)$ כלומר, ההסתברות של $A$. מספר זה מקודד את הידע או האמונה שלנו על ה״סבירות״ הקבוצתית של אלמנטים בקבוצה זו. חוק ההסתברות חייב למלא פרמטרים שונים שאפרט עליהם בהמשך .

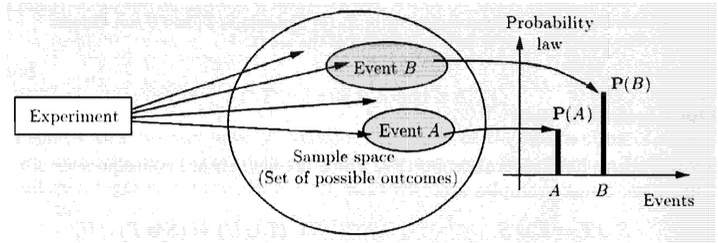
מרחב מדגם ומאורעות

כל מודל הסתבורתי מערב בתוכו תהליך בסיסי שנקרא ניסוי. הניסוי יפיק בידיוק תוצאה אפשרים אחת מבין כל התוצאות. קבוצת כל התוצאות האפשריות נקרא מרחב מדגם. תת קבוצה של מרחב מדגם נקראת מאורע. מעבר לכך אין הגבלה על מה מהווה ניסוי. למשל, אני יכול להגיד שניסוי יהיה זריקה בודדת של מטבע או 3 זריקות של מטבע או אינסוף זריקות של מטבע. אבל_ , חשוב לשים לב שבניסוח שלנו למודל הסתברותי יש רק ניסוי אחד. כלומר זריקה של שלוש מטבעות היא ניסוי בפני עצמו ולא שלושה ניסויים. מרחב המדגם יכול להכיל מספר סופי או אין סופי של תוצאות.
כמובן שמרחבים סופיים הם יותר פשוטים להבנה מתמטית אבל חשוב לשים לב שמרחבי מדגם עם מספר אינסופי של תוצאות הם קיימים וישנים הרבה מאלה. לדוגמה : זריקת חץ למטרה שהיא ריבוע בגודל $1\times 1$, כאשר נקודת הפגיעה היא התוצאה.

בחירת מרחב מדגם

אלמנטים שונים במרחב המדגם צריכים להיות זרים וסותרים אחד את השני כלומר אם תוצאה אחת במרחב המדגם קרתה השני בוודאות לא קרתה.
ישנם מספר דרכים שניתן למדל מצב כלשהו בהתאם לשאלה שנרצה לענות עליה. באופן כללי, מרחב המדגם של מודל ההסתברות צריך להיות ממצה באופן קולקטיבי, כלומר שלא משנה מה קרה בניסוי יש איזשהי תוצאה בכלולה במרחב המדגם והיא מתארת את מה שקרה. בנוסף, מרחב המדגם צריך להיות מספיק מפורט כדי להפריד בין כל התוצאות האפשריות האלה תוך המנעות מפרטים לא רלוונטים.
כל תת קבוצה של מרחב המדגם כולל הוא עצמו והמשלים שלו יכולים להיחשב כמאורעות. אם להסתכל על הסוגייה מעיניים נוקשות יותר, חלק מהקבוצות חייבות להיות לא כלולות ובאופן פרטני יותר כשמתמקדמים במודל הסתברותי שמכיל מרחב מדגם אינסופי. ישנם מקרים חריגים של תתי קבוצות במקרה כזה שהן אינן יכולות להניב הסתברויות רלוונטיות ומשמעותיות. לא נתמקד במקרים כאלה וניתן להתעלם מהם לחלוטין.

מודלים סדרתיים

לניסויים רבים יש באופן מורש תכונות סדרתיות, למשל, הטלת מטבע שלוש פעמים. במצב כזה, נהוג ושימושי לתאר את הניסוי ומרחב המדגם שלו בצורה מבוססת עץ רציף.

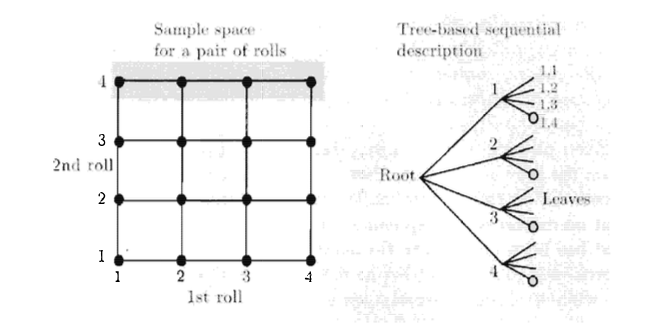
בתמונה ניתן לראות שתי תיאורים שקולים של מרחב מדגם של הניסוי הכולל הטלת קובייה עם ארבע פאות. התוצאות האפשריות מתוארות כזוג סדור $(i,j)$. כאשר $i$ זוהי תוצאת ההטלה הראשונה ו $j$ זאת תוצאת ההטלה השנייה. ניתן לתאר אותן כגריד דו מימדי כמו בתמונה השמאלית או כעץ כמו בתמונה הימנית. מרשמים אלו מתארים את תכונות המודל הבדיד של הניסוי. כל התוצאות האפשריות נמצאות בעלים והמסלול מהשורש עד לאותו עלה הוא ייחודי. במקרה של התמונה השמאלית כל נקודה מייצגת זוג סגור שהוא אחת התוצאות במרחב המדגם.

חוקי הסתברות

נניח שיש לנו מרחב מדגם $\mathrm{\Omega }$ המייצג ניסוי כלשהו. כדי להשלים את המודל ההסתברותי עלינו להציג את חוקי ההסתברות.
באופן אינטואיטיבי זה מייצג את ה״סבירות״ של כל תוצאה או אוסף של תוצאות אפשריות. באופן מדוייק יותר, חוק ההסתברות מצמיד לכל אירוע $A$ , מספר $P(A)$ שנקרא הסתברות של $A$ .

אקסיומות הסתברות

חוק הסתברות צריך לקיים את האקסיומות הבא

1. אי שליליות - ${\mathrm{\forall }}_{A\in \mathrm{\Omega }}:P(A)\ge 0$
2. נורמליזציה- $P(\mathrm{\Omega })=1$
3. אדטיביות- (בהינתן מאורעות זרים $A,B$)

נוכל לתאר חוק הסתברות באופן ויזואלי. נחשוב על יחידה מסה שנקראה לה ״התפרסות״ לאורך מרחב המדגם. $P(A)$ אם כן, הוא פשוט המסה הכוללת שהוקצתה לו או הפריסה שלו במרחב המדגם. באופן הזה אדטיביות הופכת להיות אינטואיבית יחסית

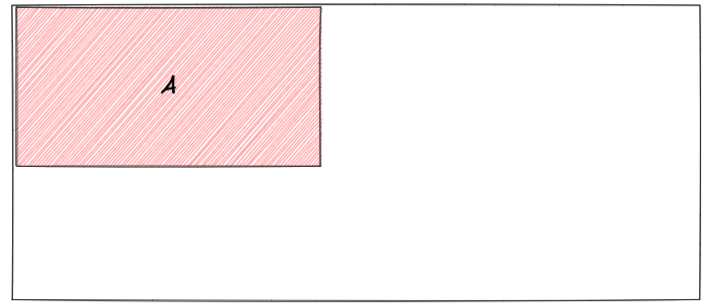
ניתן גם לתאר חוק הסתברות כעניין יחסי : אם $P(A)=\frac{2}{3}$ אז זה מייצג את האמונה שמאורע $A$ יתרחש ב $\frac{2}{3}$ מהמקרים מתוך מספר רב מאוד של חזרות על הניסוי.
התייחסויות כאלה, למרות שהן לא תמיד מתאימות, יכולות לעתים לעזור לתת אינטואיציה לקונספטים מורכבים.

מהאקסיומות ניתן להסיק כי

מודל הסתבורתי בדיד

ראשית אציג אילוסטרציה לבנייה של חוק הסתברות מהיגיון לגבי המודל.
נגדיר את הניסוי שכולל הטלה יחידה של מטבע. יש שתי תוצאות אפשרויות $H,T$ ומרחב המדגם הוא $\mathrm{\Omega }=\{H,T\}$.
המאורעות האפשריים

אם המטבע הוא הוגן כלומר ההסתברות שצד אחד יצא זהה להסתברות שהצד השני יצא בהטלה, אז אנחנו יכולים להגיד את חוק ההסתברות הבא

ולפי אקסיומת האדטיביות יתקיים

חוק ההסתברות שבנינו מקיים את האקסיומות כדרוש.

חוק ההסתברות הבדיד

כלומר לפי מה שראינו משתמע מאקסיומת האדטיביות הדבר הבא
בהינתן $nֿ\in \mathbb{N}$ תוצאות במרחב המדגם :

חיזוק לטענה הנ״ל $k$ יכול להיות גם עוצמה בת מנייה ${\mathrm{\aleph }}_0$.

במרחב מדגם שווה הסתברות יתקיים

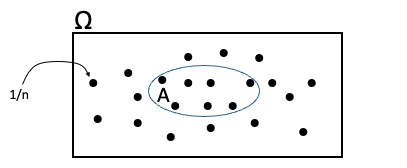
חוק ההסתברות במרחב שווה הסתברות בדיד

אם במרחב המדגם יש $n$ תוצאות שכולן בעלות הסתברות שווה, אזי יתקיים עבור מאורע $A$

דוגמה טובה למרחב כזה הוא הטלת זוג קוביות הגונות עם 4 צדדים ולכן לכל זוג סדור $(i,j)$ שמייצג תוצאה אפשרית יש את אותה הסתברות $\frac{1}{16}$ . ניתן כעת להסתכל על התרשים שעשינו למעלה כדי לתאר מרחב כזה ופשוט לספור את איברי הקבוצה שמקיימים את התנאים הדרושים למשל :

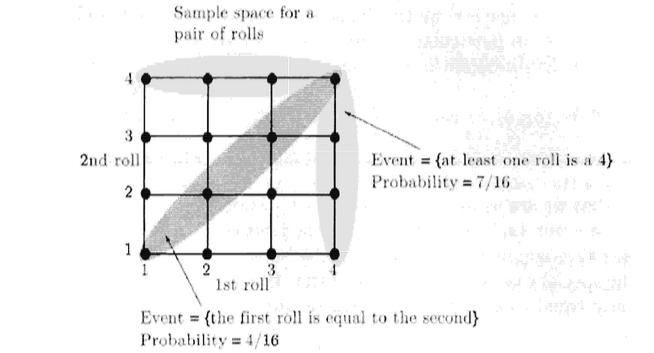
מודל הסתבורתי רציף

מודל הסתבורתי עם מרחב מדגם רציף שונה מאוד מהמודל הבדיד בכך שההסתבורות של מאורע עם איבר בודד עלול שלא להספיק כדי לאפיין חוק הסתברות.
לדוגמה: נדמיין גלגל מזלות שכל נקודה שבה הוא עוצר היא מספר בין $[0,1]$. נניח גם שהגלגל הוגן ולכל נקודה הסתברות שווה. כעת נחשוב, מה ההסתברות של מאורע עם תוצאה אפשרית אחת במרחב המדגם הזה. בוודאות היא לא יכולה להיות חיובית כי אם היא הייתה כזאת למשל $\frac{1}{n}$ כלשהו, אז נוכל לקחת מספיק איברים במרחב המדגם ולפי אקסיומת האדטיביות נקבל הסתברות של מאורע שגדול מ1 בסתירה. לכן, ההסתברות של תוצאה אחת במרחב המדגם הזה היא $0$.
במקרה הזה נוכל להגדיר חוק הסתברות $b-a$ לכל תת קטע סגור $[a,b]$ כלומר ״אורך״. ההגדרה הזאת תקיים את אקסיומות ההסתברות.

נתבונן בדוגמה נוספת:
לרומאו ויוליה יש דייט בזמן כלשהו, כל אחד מהם יגיע למקום המפגש בדיליי של בין 0 ל1 שעות. כך שלכל זוג סדור $(r,j)$ שמייצג איחור של שניהם יש הסתברות שווה. כמו כן ניתן הגבלה נוספת, אם אחד מהם מגיע וממתין 15 דקות לשני, הוא יעזוב את הדייט. מה ההסתברות שהם ייפגשו?
נסתכל על מרחב המדגם כריבוע היחידה כשכל נקודה בו מייצגת את הזוג הסדור. בגלל שזה מרחב מדגם שווה הסתברות רציף אז נוכל לפרש את ההסתברות של מאורע כלשהו או תת קבוצה של $\mathrm{\Omega }$ להיות שווה לשטח שלו בתוך ריבוע היחידה.
חוק ההסתברות הזה מקיים את שלושת האקסיומות שלנו.
כלומר אם נסמן את המאורע שהם ייפגשו כ$M$ שטחו ייראה כך :

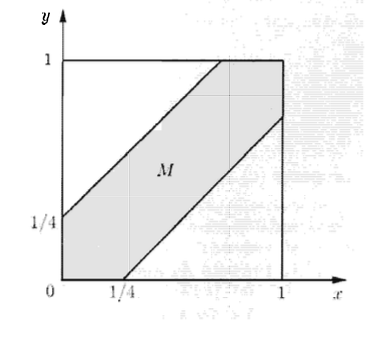
כעת נוכל לחשב את השטח ולראות שההסתברות שהם ייפגשו היא $\frac{7}{16}$. נשים לב שכשמתכוונים לשטח הכוונה היא לשטח ביחס למרחב המדגם. במקרה הזה מרחב המדגם הוא ריבוע היחידה אז לקחנו את $S_m$ וחילקנו ב $S_{\mathrm{\Omega }}=1$ .

תכונות של חוקי הסתברות

ישנן כמה תכונות של חוקי הסתברות שנובעות מהאקסיומות

הוכחה: נניח בשלילה שקיימות מאורעות כנ״ל שיקיימו $P(A)\ge P(B)$ ומכאן שיתקיים

מכיוון ש $A$ מוכל ב $B$ יתקיים

ולכן

אבל מתקיים גם ש $A\cup \bar{B}\subseteq \mathrm{\varnothing }$ בסתירה לכך שזה גדול מ1, כלומר ייתכן רק שיוויון אבל שיווין יתקיים רק אם $A=B$.

אנחנו יודעים מהאקסיומות שהמקרה הפרטי עבור קבוצות זרות יקיים את הנ״ל כי החיתוך הוא הקבוצה הריקה שהסתבורות היא 0 .

נגדיר את $A\cup B$ באופן הבא

הנ״ל הן איחוד של קבוצות זרות.
כעת נוכל להגדיר ש

כעת נשים לב שיתקיים

ובאופן דומה גם על

סך הכל נאחד את הביטוי למעלה ונקבל

מסקנה מתבקשת:
3)

ההוכחה של הנ״ל די דומה להוכחה הקודמת לה פשוט מגדירים את האיחוד על 3 קבוצות ולא על שתיים

את התכונות הנ״ל ניתן להמחיש באופן ויזואלי על ידי שימוש ב Venn diagrams. כמו כן נשים לב שניתן להכליל את $3$ באופן הבא:

ההוכחה לכך די פשוטה, פשוט נסתכל על האיחוד הגדול הזה כאיחוד של 2 קבוצות כל פעם (או להוכיח באינדוקצייה).

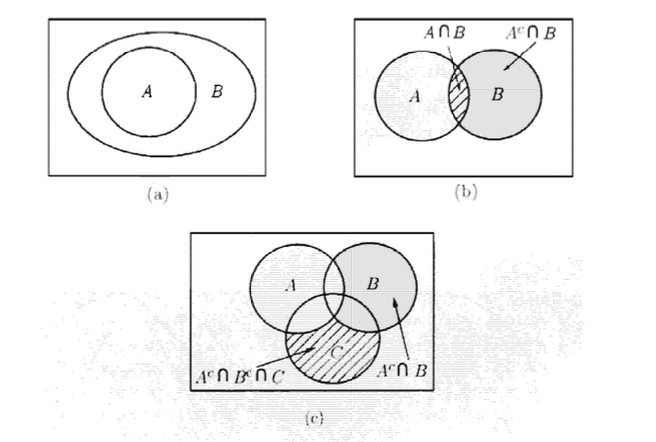
הדיאגרמות המתארות באופן ויזואלי את ההוכחות שלמעלה. למשל מדיאגרמה c אפשר לראות ש

המודלים ההסתברותיים והמציאות

המסגרת של תאוריית ההסתברות יכולה להיות שימושים כדי לנתח אי וודאות באירועים שונים עם קונטקסט פיזי.
כדי לעשות זאת מעורבים שתי שלבים עיקריים

1. בנייה של מודל הסתברות על ידי פירוט חוקי ההסתברות על מרחב מדגם מוגדר היטב. אין חוקים מולחמים כדי להנחות בשלב זה חוץ מהדרישות שחוקי ההסתברות יקיימו את האקסיומות. במקרים רבים לפעמים המודל שייבחר יהיה שגוי יותר ממודל אחר אם הוא פשוט יותר ממנו ומאפשר חישובים סבירים יותר. זה טכניקה ידועה בתחום המדעים וההנסה, שהבחירה במודל לעתיתם קשורה בהחלפות בין דיוק, פשוט ועקביות.

2. בשלב זה, נעבור בתוך מודל הסתברותי ונפתח את הסתברויות האירועים שנרצה או שנפתח כמה תכונות חשובות לגבי המודל. בעוד שהשלב הראשון הוא די פתוח לפרשנות, ברגע שהמודל סגור ומוגדר היטב אין מקום לספקולציות ומושפע ישירות מהאקסיומות והחוקים שהגדרנו קודם לכן. חשוב לזכור שגם אם החישוב מסובך, ברגע שיש מודל הסתברות מוגדר היטב לניסוי, ניתן להגיע לכל מאורע אפשרי עם יכולת והכלים הנכונים.

בתאוריית ההסתברות יש המון פרדוקסים שחישובים שונים נותנים תוצאות שונות לאותה שאלה. אבל לרוב זה קורה בכלל מודל הסתברותיים שגואים או דו משמעיים. דוגמה טובה למודל שגוי כזה הוא Bertrand's paradox