#probability #computer_science

אי תלות בין משתנים מקריים רציפים

בדומה ל מקרה הבדיד נאמר ששתי משתנים מקריים רציפים $X, Y$ הם בלתי תלויים אם ה PDF המשותף שלהם הוא תוצר של הPDF השוליים:

f_{X, Y} (x, y) = f_{X} (x) f_{Y} (y)

מהנוסחה של PDF מותנה $f_{X, Y} (x, y) = f_{X | Y} (x | y) f_{Y} (y)$ אנחנו למדים שמשמעות הדבר באי תלות היא ש

f_{X | Y} (x | y) = f_{X} (x)

ובאופן סימטרי

f_{Y | X} (y | x) = f_{Y} (y)

Info

מה שזה אומר בעצם היא שלכל ערך $y$ או $x$ שניקח בהתאמה לפונקציות הנ״ל, החתיכה שנקבל שקולה ל $f_{X} (x)$ או $f_{Y} (y)$ בהתאמה.

ההכללה למקרה של יותר משתי משתנים היא די אינטואיטיבית למשל עבור המקרה של 3 משתנים נאמר :

f_{X, Y, Z} (x, y, z) = f_{X} (x) f_{Y} (y) f_{Z} (z)

אם $X, Y$ הם בלתי תלויים, אז כל שתי מאורעות מהצורה ${X \in A} and {Y \in B}$ הם בלתי תלויים. אכן,

\begin{matrix} P (X \in A, Y \in B) = \int_{X \in A} \int_{Y \in B} f_{X, Y} (x, y) d x d y \\ = \int_{X \in A} \int_{Y \in B} f_{X} (x) f_{Y} (y) d x d y \\ = \int_{X \in A} f_{X} (x) d x \int_{Y \in B} f_{Y} (y) d y \\ = P (X \in A) P (Y \in B) \end{matrix}

באופן ספציפי נקבל מהנ״ל

F_{X, Y} (x, y) = P (X \leq x, Y \leq y) = P (X \leq x) P (Y \leq y) = F_{X} (x) F_{Y} (y)

בגלל הקשר של CDF למשתנה מקרי רציף ובדדי כאחד, אנחנו יכולים להגיד שהנ״ל מהווה איזשהו משפט הגדרה לאי תלות בין שתי משתנים באופן כללי , בלי תלות לסיווגם.

תכונה חשובה נוספת היא ש

E [g (X) h (Y)] = E [g (X)] E [h (Y)]

ומזה כמובן משתמע המקרה הפרטי של פונקצייה הזהות

E [X Y] = E [X] E [Y]

משתנים נורמלים בלתי תלויים

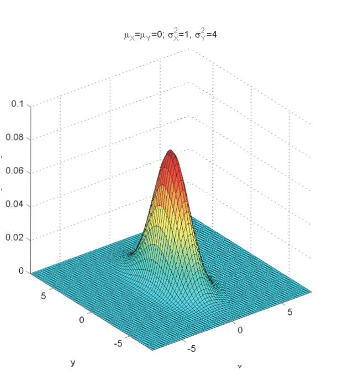
יהיו $X, Y$ משתנים נורמלים בלתי תלויים עם תוחלות $μ_{x}, μ_{y}$ בהתאמה ושונות $σ_{x}^{2}, σ_{y}^{2}$ בהתאמה. נקבל הפונקציית הצפיפות המשותפת תהיה

f_{X, Y} (x, y) = f_{X} (x) f_{Y} (y) = \frac{1}{2 π σ_{x} σ_{y}} \cdot e^{- \frac{(x - μ_{x})^{2}}{2 σ_{x}^{2}} - \frac{(y - μ_{y})^{2}}{2 σ_{y}^{2}}}

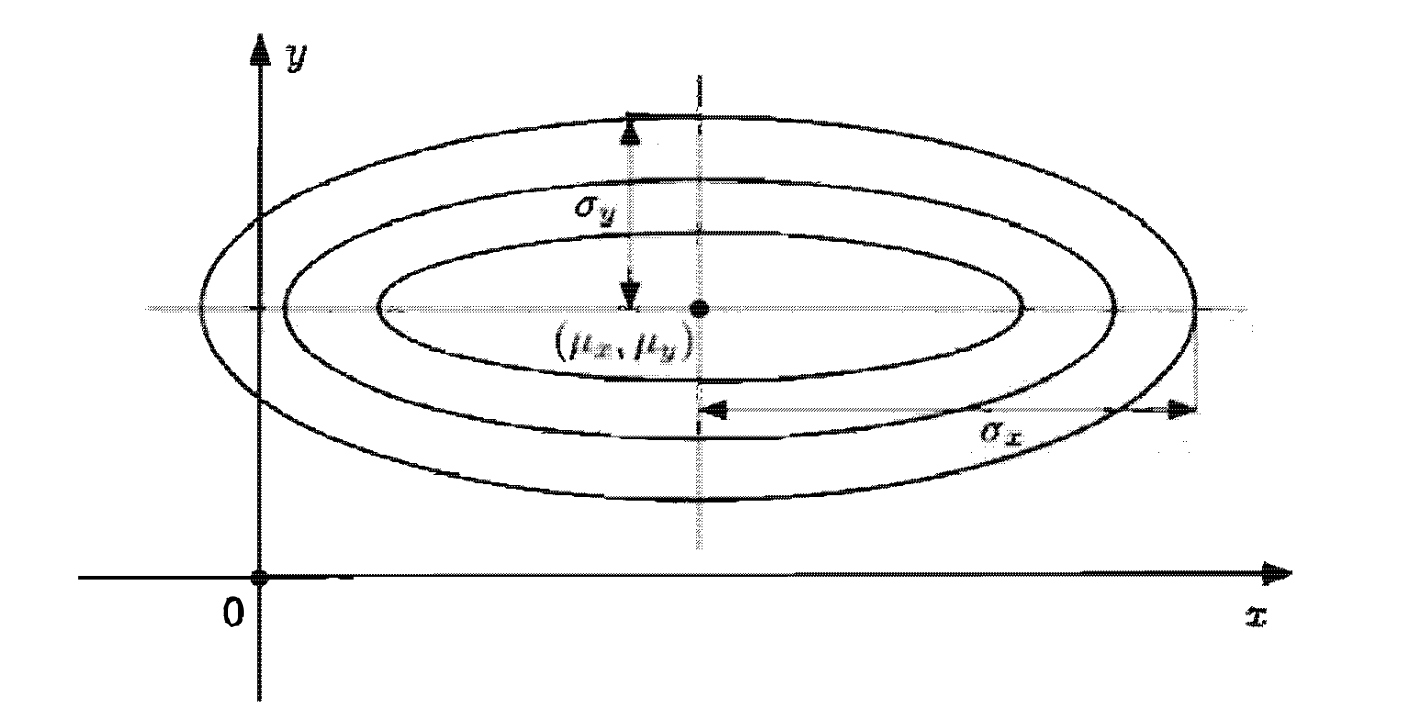
הPDF המשותף הוא מעין צורת פעמון כאשר המרכז הוא $μ_{x}, μ_{y}$ . כמו כן באמצעות קווי המתאר כלומר בהינתן קבוע כלשהו קו מתאר מסויים יהיה מצב שבוא

f_{X, Y} (x, y) = c o n s t a n t

במקרה שלנו נוכל להמיר את זה למצב שבו

\frac{(x - μ_{x})^{2}}{2 σ_{x}^{2}} + \frac{(y - μ_{y})^{2}}{2 σ_{y}^{2}} = constant

כי רק במעריך יש תלות במשתנים.

אם כן, נקבל שקווי המתאר האלה הם אליפסות במישור הדו מימדי ובמצב שבוא $σ_{y} = σ_{x}$ למשל אם שניהם היו סטנדרטים , היינו מקבלים מעגל.

Pasted image 20230126115003.png|300

Pasted image 20230126115014.png