#probability #computer_science

משתנים רנדומיים-בדיד

מהו משתנה אקראי

ברוב המודלים ההסתברותיים שנבנה התוצאות הדרושות יהיו ערך מספרי של ממש (כמו קריאה של מנייה). למרות זאת ישנם ניסויים, שבהם התוצאה היא לא משהו מספרי אבל נוכל לשייך את התוצאה של הניסוי לערך מספרי שמעניין אותנו. דוגמה טובה לכך תהיה אם הניסוי הוא בחירה של סטודנטים מאוכלוסייה מסויימת. אולי נרצה להתייחס לממוצע שלהם למשל. כנרצה להתייחס לערכים כאלה אנחנו נותנים להסתברויות שמייצגות מאורעות כלשהו את הערך המתאים הנ״ל. זה נעשה באמצעות משתנים רנדומיים.

הגדרה : בהינתן ניסוי ומרחב מדגם, משתנה רנדומי משייך מספר עם תוצאה. באופן מתמטי ,
משתנה רנדומי $X$ הוא פונקצייה מתמטית מ $Ω$ ל $R$ . שתקיים $X (A) = x$ .

נשים לב שהסימון הוא $X$ עבור המשתנה הרנדומי ו $x$ עבור ערך אפשרי שלו.

דוגמאות :

ניסוי שיש 5 הטלות של מטבע. נוכל להגיד משתנה רנדומי שקובע את מספר הפעמים שקיבלנו ערך כלשהו .
ניסוי שבו מטילים קובייה נוכל להגדיר משתנה רנדומי שקובע את סכום שתי ההטלות, מספר הפעמים שהיה 6 בשתי ההטלות וכו.

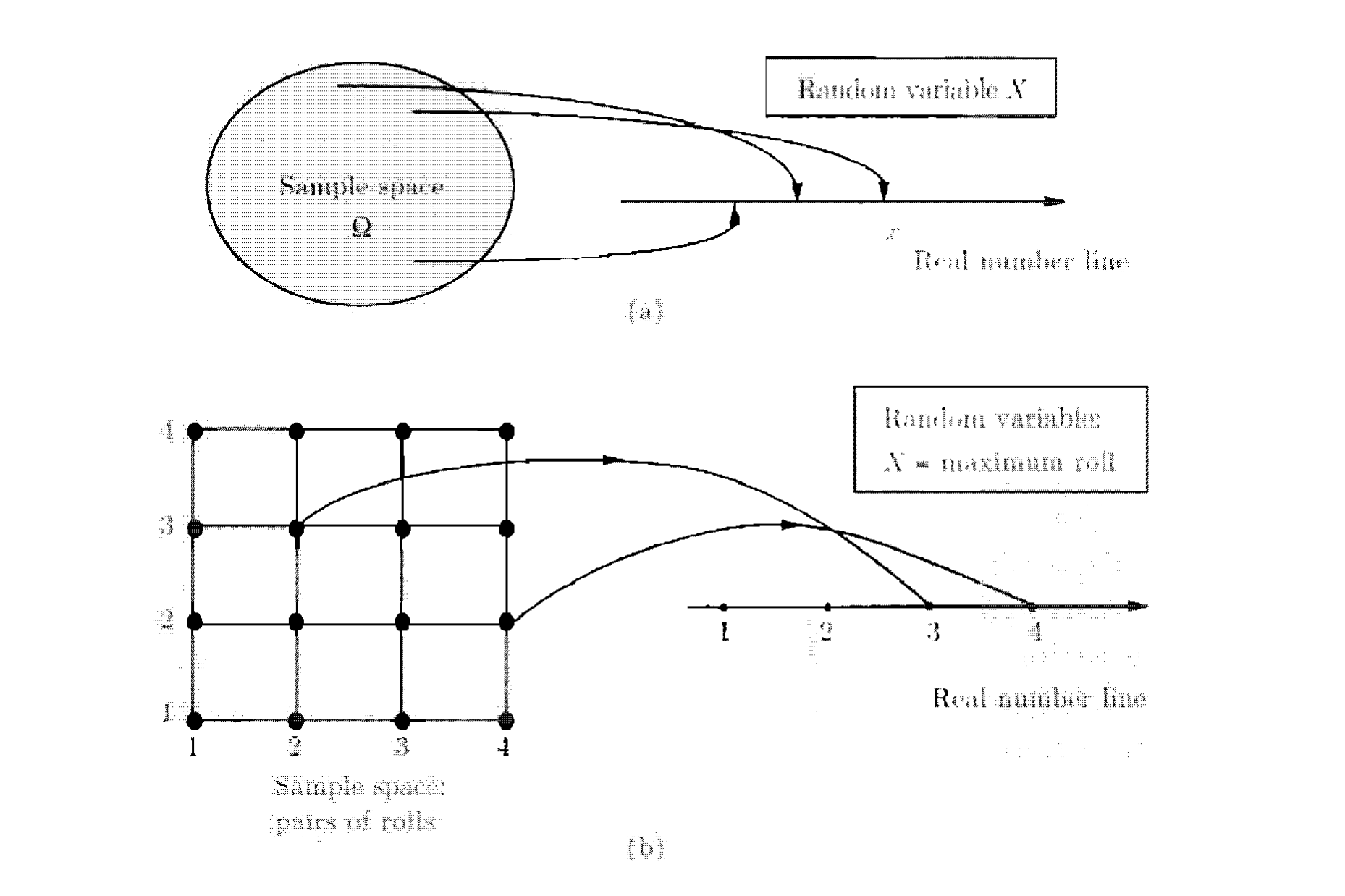
Pasted image 20221117010630.png|450

ישנם מספר קונספטים בסיסיים שצריך להכיר כשעבודים עם משתנים רנדומיים

משתנים אקראיים - הוא פונקצייה ממרחב המדגם לממשיים.
פונקציה של משתנים רנדומים היא גם משתנה רנדומי. לדוגמא, נתונים X ו-Y משתנים רנדומים אזי X+Y גם הוא משתנה רנדומי
נוכל לשייך למשתנה רנדומי ״ממוצע״ מסויים שיעניין אותנו כמו תוחלת ו variance.
משתנים רנדומיים יכולים להיות מותנים במאורע מסויים או משתנה רנדומי אחר.
ישנה אפשרות ל אי תלות של משתנה רנדומי עם מאורע או עם משתנה רנדומי אחר.

משתנה רנדומי בדיד

משתנה רנדומי ייקרא בדיד אם הטווח של הפונקצייה שלו הוא סופי אם בן מנייה. למשל משתנה רנדומי שהטווח שלו הוא ${1, 2, 3, 4}$ או $N$ הוא בדיד. משתנה רנדומי שהטווח שלו הוא $[0, 1]$ הוא רציף כי זאת קבוצה עם עוצמה החזקה מ $ℵ_{0}$ .

ישנם מספר קונספטים חשובים בכל הקשור למשתנה רנדומי בדיד

פונקציית המסה או פונקצייה ההסתברות (PMF) נותנת להסתברות לכל ערך בתחום של המשתנה הרנדומי.
פונקציה של משתנים רנדומים בדידים היא גם משתנה רנדומי בדיד. הPMF שלו יכול להיות מושג מה PMF של המשתנה המקורי.

PMF

הדרך הטובה ביותר לאפיין משתנה רנדומי היא דרך ההסתברויות שכל ערך מקבל. יהי משתנה רנדומי $X$ , נשיג את ההסתברויות האלה על ידי $P M F$ פונקציית מסת ההסתברות של $X$ . הסימון לפונקצייה זו היא $p_{X} (x)$ . וההגדרה המתמטית שלה היא

p_{X} (x) = P ({X = x}) = P ({w \in Ω | X (w) = x})

ניתן גם לסמן $P (X = x)$

כלומר פונקציית מסת ההתסברות לערך $x$ של משתנה רנדומי $X$ תחזיר את ההסתברות של המאורע המייצג את כל התוצאות האפשריות ש $x$ הוא הערך שלהן ביחס למשתנה הרנדומי $X$ .
לדוגמה, נסתכל על ניסוי שמכיל שתי הטלות בלתי תלויות של מטבע הוגן ונגדיר את $X$ להיות מספר הפעמים שיצא head. פונקציית ה PMF תהיה:

p_{X} (x) = {\begin{cases} \frac{1}{4} & x = 0 \lor x = 2 \\ \frac{1}{2} & x = 1 \\ 0 & e l s e \end{cases}

תכונות ל PMF

$\sum_{x} p_{X} (x) = 1$ זה נובע מאקסיומות ההסתברות והעובדה ש $X$ היא פונקצייה שהתמונה ההפוכה שלה היא מרחב המדגם ולכן ישנו מיפוי של כל התוצאות האפשריות והחלק היחסי שלהן מקבל הסתברות באמצעות pmf.
לכל קבוצה $S$ של ערכים אפשריים של ערכים אפשריים של $X$ יתקיים $P (X \in S) = \sum_{x \in S} p_{X} (x)$

חשוב להסביר רגע את הסימון, הוא מייצג את ההסתברות ש $x$ כלשהו שייך לקבוצה $S$ .
למשל אם נסתכל על ניסוי מהדוגמה למעלה, ההסתברות שיהיה לפחות head אחד הוא :

P (X > 0) = P ({x \in X | x > 0}) = \frac{1}{2} + \frac{1}{4} = \frac{3}{4}

חישוב PMF של משתנה רנדומי X

לכל ערך x ששייך ל X נעשה את הדבר הבא

נאסוף את כל התוצאות האפשריות לניסוי שמקיימות את המאורע ${X = x}$ .
נסכום את ההסברויות שלהם כדי לקבל $p_{X} (x)$

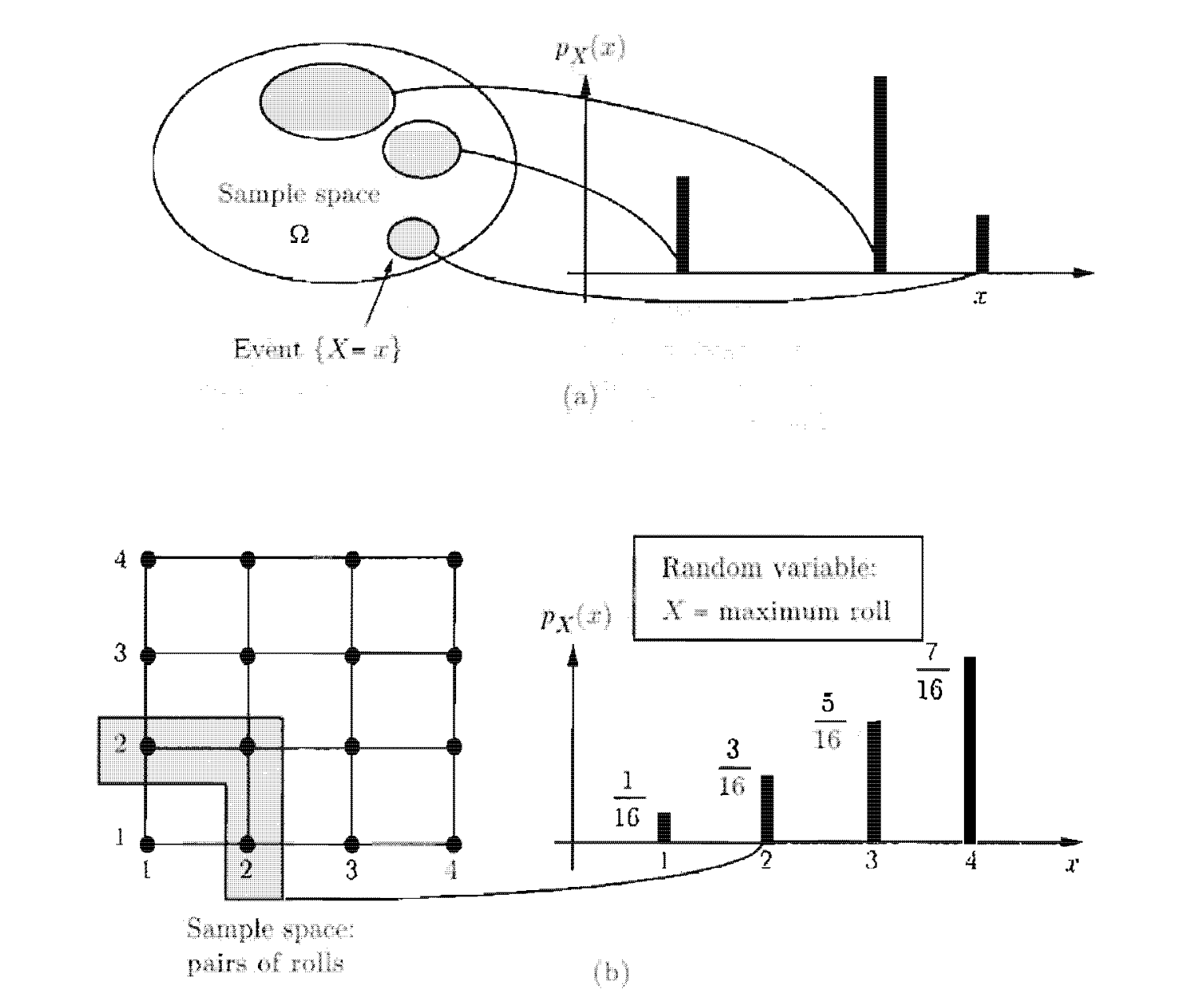
Pasted image 20221117195222.png|450

סוגים של משתנים רנדומים בדידים

משתנה ברנולי

נניח שמטילים מטבע שבהסתברות p ייתן לנו head וב $1 - p$ ייתן tail. משתנה ברנולי לוקח שתי ערכים : 1,0 ומשייך אותם לאחת התוצאות בהתאם

X = {\begin{cases} 1 & head \\ 0 & tail \end{cases}

ה pmf שלו זה

p_{X} (k) = {\begin{cases} p & k = 1 \\ 1 - p & k = 0 \end{cases}

המשתנה הזה אומנם פשוט אבל הוא חשוב מאוד. בפרקטיקה, משתמשים בו למידול תרחישים הסתברותיים גנרים עם שתי תוצאות בלבד. למשל:

המצב של טלפון בכל רגע נתון יכול להיות פנוי או תפוס.
בן אדם יכול להיות חולה או לא חולה במחלה מסויימת.

יתרה מכך, שילוב של מספר משתני ברנולי מאפשר בנייה של משתנה רנדומי מורכב יותר למשל משתנה בינומי.

משתנה אינדיקטור

משתנה מקרי אינדיקטור הוא מקרה פרטי של ברנולי , אפשר להגיד שהוא גם משתנה שעוזר לתאר התפלגות ברנולי. הוא מוגדר על מאורע $A$ ומסומן $I_{A}$ ומקבל את הערכים $0, 1$ כאשר

P (I_{A} = 1) = P (A), P (I_{A} = 0) = P (A^{c})

באמצעות משפטים שקשורים לתוחלת עליה נדבר בהמשך נוכל להוכיח שעבור מאורעות תלויים, אם נוכל להפריד אותם לרצף של אינדיקטורים, אזי נוכל לחשב כל מיני סוגים של מידע על המאורעות באמצעות תכונות של אינדיקטורים.

משתנה/התפלגות בינומי

זורקים מטבע $n$ פעמים. בכל הטלה נקבל head בהסתברות p ו tail בהסתברות $1 - p$ . ההטלות הן בלתי תלויות. נגדיר את $X$ להיות מספר ה heads בסדרה של $n$ הטלות.
מתייחסים ל $X$ כמשתנה בינומי אקראי עם פרמטרים $n, p$ . פונקציית ה PMF של $X$ מכילה את ההסתברות הבינומית שחישבנו במבחני אי תלות .

p_{X} (k) = P (X = k) = (\binom{n}{k}) p^{k} (1 - p)^{n - k}

כאשר k מייצג את המספר אותו נרצה למצוא. נשים לב שהתכונה שרצינו מתקיימת שהסכום של כל הקלטים האפשריים בפונקציית הpmf תיתן 1 (הוכחנו את זה על הנוסחה הזאת).

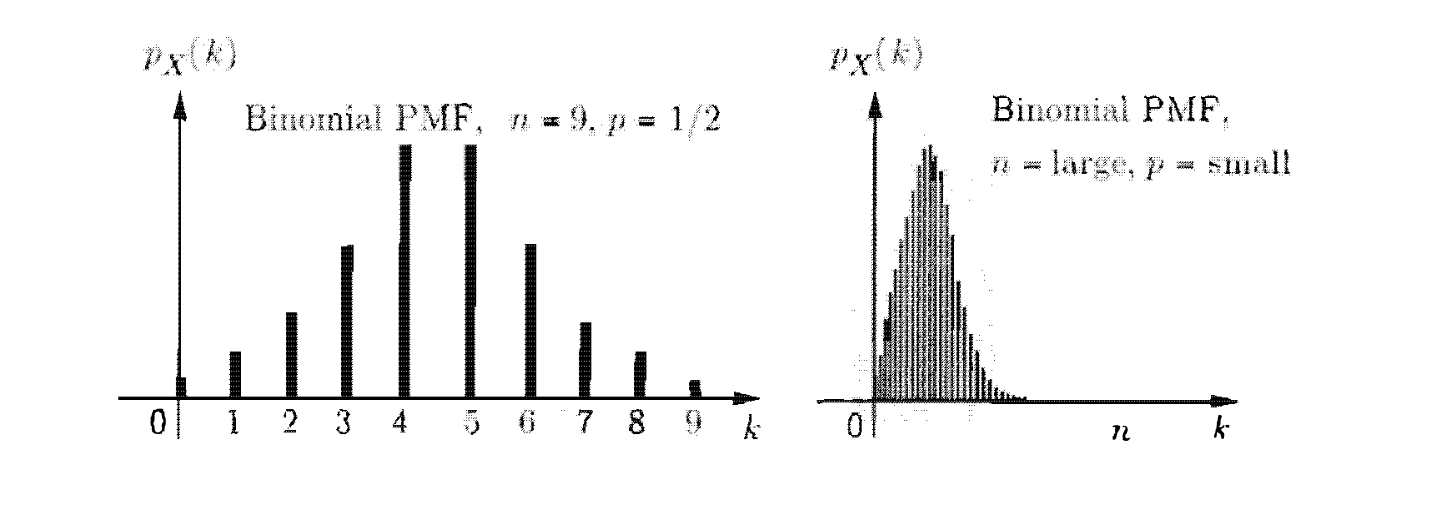
Pasted image 20221117200351.png
כאן ניתן לראות שתי מצבים מעניינים של pmf . הראשון הוא כאשר p=0.5 שבו ניתן לראות שההתפלגות של הערכים היא סימטרית ביחס ל $\frac{n}{2}$ . בכל מצב אחר היא מוטת ל0 אם $p < \frac{1}{2}$ או ביחס ל $n$ אם $p > \frac{1}{2}$ ( כפי שניתן לראות בתמונה).

אינטואיציה

הסיבה שפונקציית מסת ההסתברות ממודלת ככה היא הגיונית למדי, שכן אם נדמיין את הדוגמה של הטלת המטבע כמודל הסתברותי סדרתי (למשל עץ) אנחנו נראה שתמיד שלקראת הערכים באמצע של $n$ (תלוי בהסתברות במקרה הזה המטבע הוגן) יהיו יותר ענפים שהסדר שלהם יקיים שקרה $k$ פעמים מה שנרצה ו $n - k$ מה שלא רצינו.

משתנה גיאומטרי

נניח שיש לנו באופן חוזר ובלתי תלוי הטלת מטבע באופן בלתי תלוי, עם הסתברות לקבל head שהיא p כאשר אנחנו יודעים בוודאות ש $0 < p < 1$ . המשתנה הגיאומטרי הרנדומי הוא $X$ ומייצג את מספר ההטלות עד שיוצא $h e a d$ פעם ראשונה. נוסחת ה pmf תהיה:

p_{X} (k) = P (X = k) = P (\underset{k-1 times}{\underset{⏟}{T T T T \dots T}} H) = (1 - p)^{k - 1} \cdot p

הנוסחה הזאת מאוד הגיונית כי היא מתארת רצף של הטלות בלתי תלויות כאשר $k - 1$ פעמים יצא tail ובפעם שרצינו יצא head (יש רק ענף אחד כזה עבור k הטלות).

\sum_{k = 1}^{\infty} p_{X} (k) = \sum_{k = 1}^{\infty} (1 - p)^{k - 1} p = p \sum_{k = 1}^{\infty} (1 - p)^{k - 1} = p \cdot \sum_{k = 0}^{\infty} (1 - p)^{k} = p \cdot \frac{1}{1 - (1 - p)} = 1

המעבר האחרון נובע בגלל שנתון ש p מספר קטן בין 0 ל 1 ולכן $1 - p$ גם מספר בטווח הזה כלומר יש לנו סכום סדרה הנדסית מתכנת ל 1 (לפי סכום סדרה הנדסית אינסופית $S = \frac{a_{1}}{1 - p}$ ).
השתמשנו בדוגמה של הטלת מטבע כי היא מתארת את המשתנה הזה באופן די טבעי. באופן כללי, נוכל לפרש משתנה גיאומטרי במונחים של חזרה בלתי תלויה של ״מבחנים״ עד ל״הצלחה״ ראשונה. כל מבחן יהיה עם הסתברות להצלחה $p$ והמידול של המשתנה נעשה על ידי כמות המבחנים שעשינו עד להצלחה (ההצלחה נספרת בכמות). נשים לב שהצלחה זה תלוי בהקשר שאנחנו מדברים עליו.
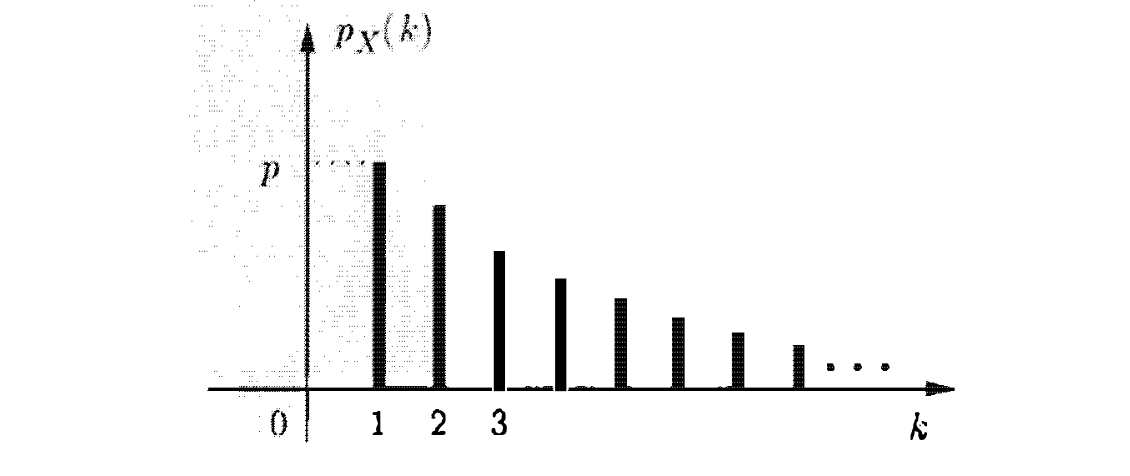
Pasted image 20221117204049.png|450
ככל ש $k$ גבוה יותר נקבל תוצאה נמוכה יותר עבור pmf.

משתנה פואסון

למשתנה פואסון יש PMF שמיוצג על ידי

p_{X} (k) = e^{- λ} \cdot \frac{λ^{k}}{k!}

כאשר $λ$ זה פרמטר חיובי שמתאר את ה PMF. אפשר להתייחס אליו גם כ ״קצב״ כלומר מספר המאורעות בכל זמן דגימה.
נשים לב ש $X$ מייצג את מספר המאורעות שמתרחשים בפרק זמן כלשהו. ו $λ$ זה הקצב הממוצע כלומר כמה מצופה שיקרה. (בגלל זה כפי שנראה מרכז המסה של פונקציית מסת ההסתברות תמיד יהיה כאשר $x = λ$ ).

זה משתנה PMF לגיטימי בגלל ש

\sum_{k = 0}^{\infty} \frac{e^{- λ} λ^{k}}{k!} = e^{- λ} (1 + λ + \frac{λ^{2}}{2!} + \frac{λ^{3}}{3!} + \frac{λ^{4}}{4!} + \dots) = e^{- λ} e^{λ} = 1

זה נובע מ טורי טיילור ידועים (הטור של הפונקצייה $e^{x}$ ).
פונקציית מסת ההסתברות עבור קלט $k$ מהווה את ההסתברות לקבל $k$ מאורעות בתוך זמן הדגימה.

כדי לקבל אינטואיציה למשתנה פואסון. נחשוב על משתנה בינומי עם מספר $p$ ממש קטן ו $n$ ממש גדול. למשל: עבור $X$ שמייצג את מספר שגיאות הכתיב בספר בספר עם $n$ מילים. אזי $X$ הוא בינומי בגלל שאנחנו רוצים לבחור $x$ מילים מתוך $n$ שלהן יהיה שגיאת כתיב. אבל ההסתברות של $p$ שמילה אחת שתבחר תהיה עם שגיאת כתיב הוא כל כך קטן, שנוכל למדל את $X$ גם באמצעות ה pmf של פואסון. באופן מדוייק יותר,פונקציית pmf של משתנה פואסון עם פרמטר $λ$ מהווה קירוב טוב ל pmf של המשתנה הבינומי.

\frac{e^{- λ} λ^{k}}{k!} ≂ \frac{n!}{k! (n - k)!} p^{k} (1 - p)^{n - k}

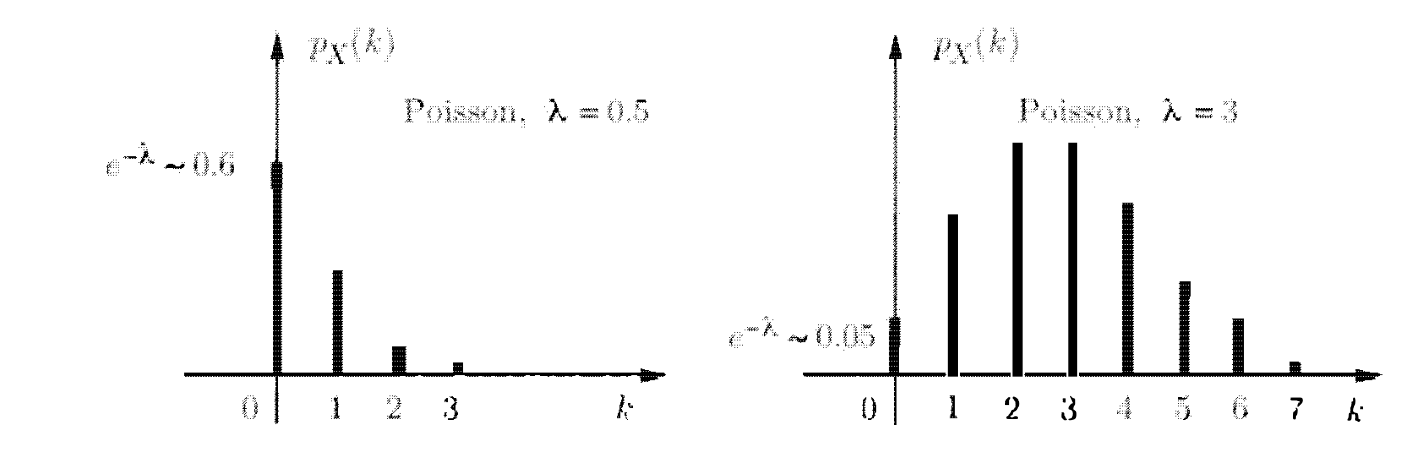
Pasted image 20221118100432.png

נשים לב, $λ = n p$ כאשר $n$ מספר גדול מאוד ו $p$ מספר קטן מאוד. במקרה הזה להשתמש במשתנה פואסון יכול לתת לנו תוצאה פשוטה יותר ומודל ברור יותר. לדוגמה, עבור $n = 100$ ו $p = 0.01$ ההסתברות לקבל $5$ הצלחות ב 100 מבחנים תהיה

\frac{100!}{95! 5!} {0.01}^{5} \cdot {0.99}^{95} = 0.00290

מאוד מעצבן לחשב, אבל על ידי שימוש במשתנה פואסון עם $λ = n p = 1$ נקבל

e^{- 1} \frac{1}{5!} = 0.00306

הקשר בין פואסון לבינומי
בדומה:

המאורעות בלתי תלויים - התרחשות של מאורע אחד באינטרוול כלשהו לא משפיע על כך שהוא יקרה מאוחר יותר.
בשתיהם יש מידול של סיכוי להצלחה והסתברות לכשלון
גם במקרה הזה אנחנו מעוניינים בהסתברות למספר הצלחות כלשהו.

בשונה:

מספר הניסויים במשתנה פואסון לא מוגדר
ההסתברות להתרחשות של מאורע בודד אינה ידועה אך ברוב המקרים בקטנה מאוד.

מה המשמעות של פואסון?

משתמשים במשתנה פואסון במצבים בהם מאורע יכול לקרות בכל רגע ולכן אין לנו הסתברות על המאורע. אם האירועים מתרחשים באופן בלתי תלוי ובקצב (ממוצע) קבוע $λ$ , אזי מספר האירועים שהתרחשו בפרק זמן נתון מתפלג פואסונית.
דוגמה לכך היא מספר השיחות המתקבלות במרכזיית טלפונים במשך דקה.
ניתן לראות את התפלגות פואסון בתור גבול של סדרת התפלגויות בינומיות שבה מספר הניסויים שואף לאינסוף, ותוחלת מספר ההצלחות נשארת קבועה.
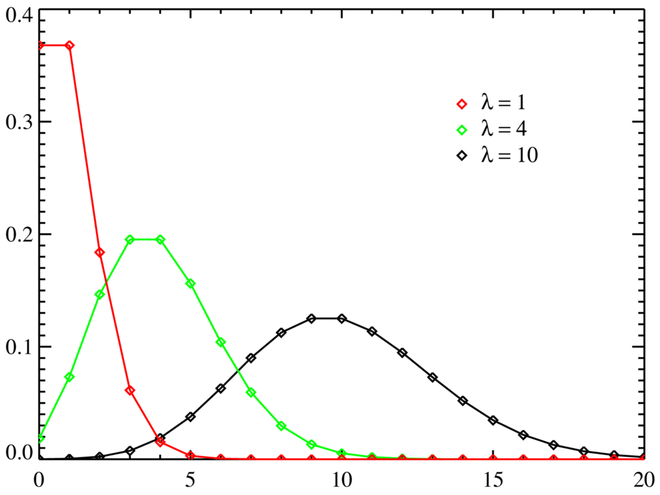
Pasted image 20230129013019.png|300

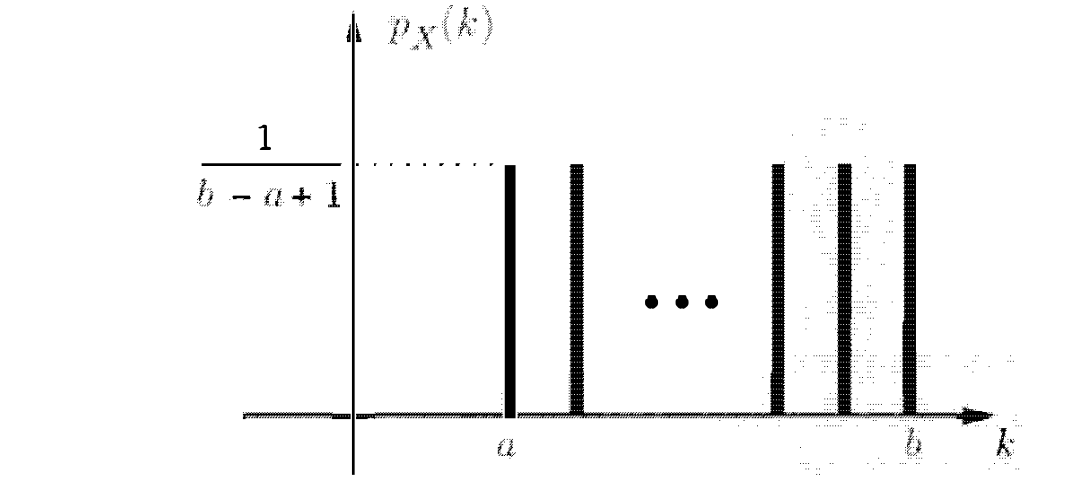
משתנה בדיד אחיד uniform

משתנה רדנומי X הוא משתנה אחיד עם פרמטרים a ו-b כאשר a ≤ b אם ערכו של המשתנה הוא מספר מ a,a+1,…,b כאשר לכל מספר ההסתברות זהה.
כלומר מרחב המדגם הוא $Ω = {a, a + 1, a + 2, \dots, b}$ המשתנה הרנדומי $X$ יקיים $X (w) = w$ . מצב זה מתאים עבור מודל שאנחנו לא יודעים מי התוצאה הרצוייה.

נשים לב ההסתברות למאורע שהתוצאה תהיה $w$ היא $\frac{1}{b - a + 1}$ (זה בעצם התוצאה האפשרית במונה חלקי מספר התוצאות במרחב המדגם). לכן זאת גם פונקציית ה PMF של משתנה כזה

p_{X} (x) = P (X = x) = P (x) = \frac{1}{b - a + 1}

כלומר מרחב המדגם הוא מרחב שווה הסתברות.

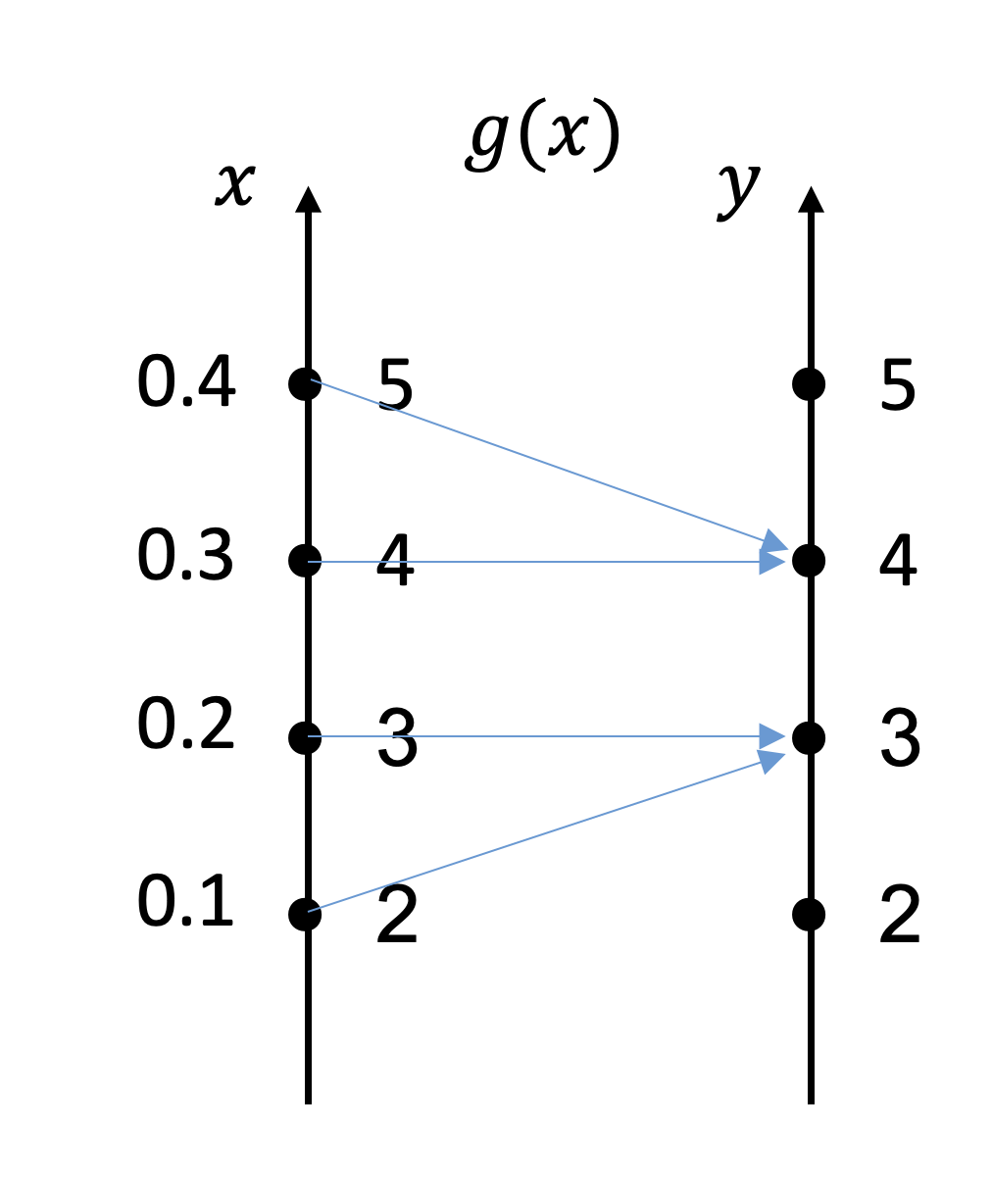
פונקציות של משתנים רנדומיים בדידים

בהינתם משתנה רנדומי $X$ , נוכל לייצ רמשתנה רנדומי אחר על ידי הפעלת טרנספורמציות על $X$ .
לדוגמה, בהינתן משתנה רנדומי $X$ שמייצג את הטמפרטורה היומית במעלות, ונגדיר $Y = 1.8 X + 32$ המשתנה שממיר את $X$ ממעלות לפרנהייט. במצב זה Y הוא פונקצייה ליניארי של X:

Y = g (X) = a X + b

כאשר $a, b$ הם סקלרים.
כמו כן נוכל להגדיר את $Y$ להיות פונקצייה לא ליניארית כלשהי. בכל מקרה, מה שחשוב להבין כאן הוא ש אם $Y = g (X)$ הוא פונקצייה של משתנה רנדומי $X$ אז $Y$ הוא בעצמו משתנה רנדומי שכן הוא מספק ערך מספרי לכל תוצאה אפשרית במרחב המדגם. זה נכון, בגלל שלכל $x \in X$ נוכל להפעיל את הפונקצייה $g$ ולקבל $y \in Y$ . כמו כן, כמובן שאם $X$ הוא משתנה רנדומי בדיד, בהכרח גם $Y$ מהגדרה של פונקציות. נוכל לחשבת את פונקציית מסת ההסתברות של Y באמצעות $p_{X}$ .

p_{Y} (y) = \sum_{{x | g (x) = y}} p_{X} (x)

כלומר, עבור קלט $y$ ההסתברות תהיה סכום כל ההסתברויות שנקבל מפונקציית מסת ההתסברות באשר $x \in i m g_{g}^{- 1} (y)$ .

דוגמה : עבור $Y = | X |$ ו

p_{X} (x) = {\begin{cases} \frac{1}{9} & x \in [- 4, 4], N \\ 0 & e l s e \end{cases}

נקבל את $p_{Y} (y)$ הבא:
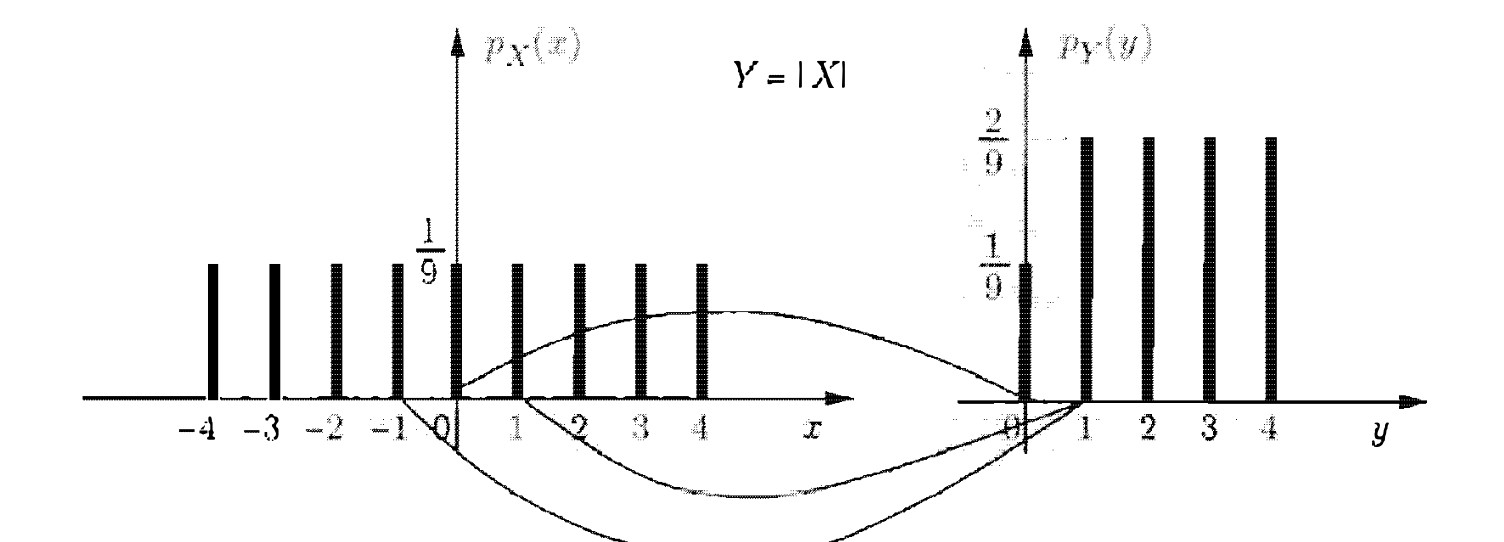
Pasted image 20221118132604.png

בגלל שלכל שתי ערכים ב $X$ בפרט ל 0 נקבל ערך אחד ב $Y$ יתקיים שפונקציית מסת ההתסברות של $Y$ תהיה

p_{Y} (y) = {\begin{cases} \frac{2}{9} & y \in [4] \\ \frac{1}{9} & y = 0 \\ 0 & e l s e \end{cases}

תוחלת ו variance (שונות)

תוחלת

פונקציית מסת ההסתברות ששל משתנה רנדומי X נותנת לנו את ההסתברויות של כל הערכים של X . הרבה פעמים נרצה את זה, אבל נרצה לעתים לכמת את המידע הזה למספר יחיד. המספר הזה הנקרא התוחלת של $X$ .שזה ממוצע משוקלל ביחס להסתברויות של כל הערכים האפשריים ב X.
כדי לקבל אינטואיצייה נניח שאנחנו מסובבים גלגל מזל מספר רב של פעמים. על כל מספר שמתקבל $m_{1}, m_{2}, m_{3}, \dots, m_{n}$ עם הסתברויות מתאימות $p_{1}, p_{2}, p_{3} \dots, p_{n}$ אתה מקבל את הערך של $m_{i}$ אם הוא יצא לך.
נרצה לדעת מה כמות הכסף שאני מצפה להשיג עבור סיבוב. ״מצפה״ ו״עבור סיבוב״ הם קצת מונחים עם מספר משמעויות אבל פרשנות סבירה להן תהיה:
אם נסובב את את הגלגל $k$ פעמים, ן $k_{i}$ הוא מספר הפעמים שקיבלת $m_{i}$ . אז הכסף שקיבלת פר סיבוב בממוצע יהיה

M = \frac{\sum_{i = 1}^{n} m_{i} k_{i}}{k}

אם $k$ הוא מספר גבוה ממש ונפרש התסברות כיחס. זה סביר להניח ש $m_{i}$ מגיע בתדירות מסויימת של פעמים שהיא בערך שקולה ל $p_{i}$

\frac{k_{i}}{k} \approx p_{i}

לפיכך, כמות הכסף פר סיבוב שאני מצפה להשיג היא

M = \frac{\sum_{i = 1}^{n} m_{i} k_{i}}{k} = \sum_{i = 1}^{n} m_{i} p_{i}

ומכאן נוכל להגדיר באופן ברור יותר את ה תוחלת : נגדיר את התוחלת של משתנה רנדומי $X$ עם פונקציית מסת הסתברות $p_{X}$ על ידי:

E [X] = \sum_{x} x p_{X} (x)

אינטואיטיבית זה עוזר להסתכל על התוחלת של $X$ כ״נציג״ של הערכים שלו, שנמצא איפהשהו באמצע של טווח הערכים הללו. אפשר לקרוא לזה ״מרכז כוח המשיכה״ של פונקציית מסת ההסתברות.
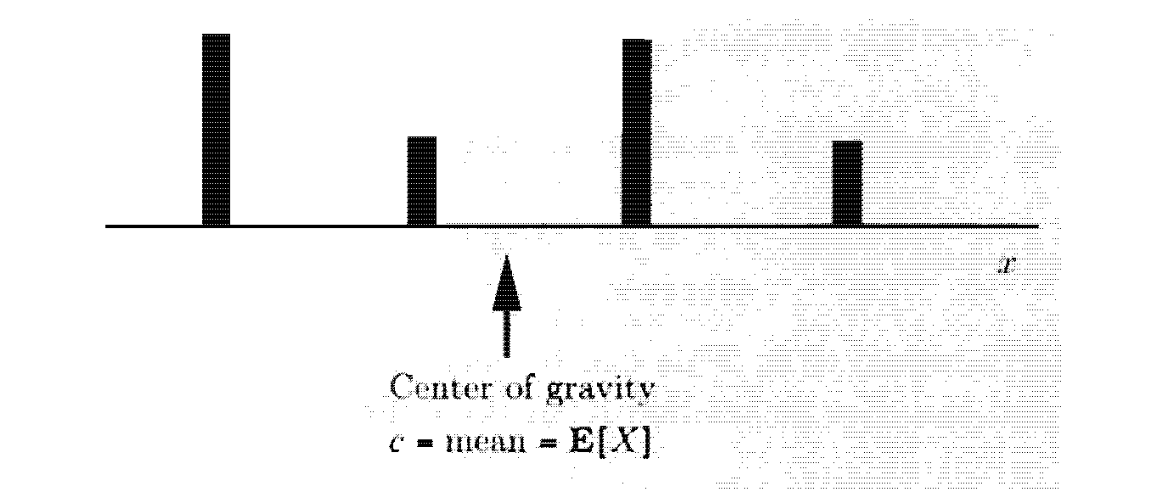
Pasted image 20221118220441.png|450
הגרף מראה מה המשמעות של מרכז כוח המשיכה. נניח שהגרף למעלה מתאר לכל נקודה $x$ את $p (x) > 0$ המתאים לה, מרכז המשיכה $c$ יהיה הנקודה שבה סכום כל האיברים משמאל יהיה שווה לסכום כל האיברים מימין כלומר

\sum_{x} (x - c) p_{X} (x) = 0

אם נפתח את זה נקבל

\sum_{x} x p_{X} (x) - \sum_{x} c p_{X} (x) = \sum_{x} x p_{X} (x) - c \sum_{x} p_{X} (x) = \sum_{x} x p_{X} (x) - c

כלומר כדי שההפרש יהיה 0 נרצה ש $c = \sum_{x} x p_{X} (x) = E [X]$

מומנט

חוץ מהתוחלת ישנם תכונות נוספות שנרצה לשייך את פונקציית מסת ההסתברות אליהם. לדוגמה מגדירים את המומנט ה2 של משתנה רנדומי $X$ כ תוחלת של המשתנה הרנדומי $X^{2}$ . באופן כללי מגדירים את ה מומנט ה $n$ י כ $E [X^{n}]$ , התוחלת של המשתנה הרנדומי $X^{n}$ . נשים לב שהתוחלת היא פשוט המומנט ה1.

variance- שונות

התכונה החשובה ביותר של משתנה רנדומי $X$ חוץ מהתוחלת נקראת השונות שלה. זאת מסומנת כ $v a r (X)$ ומוגדרת ע״י

var (X) = E [(X - E [X])^{2}]

כלומר היא מוגדרת להיות התוחלת של המשתנה הרנדומי $(X - E [X])^{2}$ (כלומר השונות היא תמיד חיובית).
השונות מספקת דרך למדוד את ההתפזרות של $X$ סביב התוחלת שלו. נוכל למדוד התפזרות זאת גם על ידי סטיית התקן של $X$ שמוגדרת כך

σ_{X} = \sqrt{v a r (X)}

נשים לב שבאופן אינטואיטיבי , השונות מייצגת את ממוצע המרחקים של כל הערכים מהמשתנה הרדנומי למרכז הכבידה שלו $E [X]$ . יותר קל לפעמים לעבוד עם סטיית התקן בגלל שהיא מחזירה אותנו לאותם יחידות מידה כמו של $X$ . למשל אם $X$ מודד מרחק במטרים אז השונות מיוצגת על ידי מטרים ריבועיים, אבל סטיית התקן מחזירה את זה למטרים.

דרך אחת לחשב את השונות היא לפי ההגדרה של תוחלת של משתנה רנדומי. זאת בהינתן שכבר יש לנו את פונקציית מסת ההסתברות של $X$ . השאלה היא כיצד
מחלצים את פונקציית מסת ההסתברות של $g (X)$ כלשהו? (במקרה הזה $g (X) = (X - E [X])^{2}$ )

נסתכל על הדוגמה הבאה כדי להתחיל לענות על השאלה הזאת
עבור המשתנה הרדנומי $X$ עם פונקצית מסת ההסתברות

p_{X} (x) = {\begin{cases} \frac{1}{9} & if x is an integer in the range [- 4, 4] \\ 0 & e l s e \end{cases}

נשים לב שיתקיים במקרה הזה שהתוחלת היא $0$ . עבור המשתנה הרנדומי $Z = (X - E [X])^{2} = X^{2}$ יתקיים

p_{Z} (z) = {\begin{cases} \frac{2}{9} & if z = 1,4,9,16 \\ \frac{1}{9} & z = 0 \\ 0 & e l s e \end{cases}

כעת אם נחשב לפי הגדרה נקבל

v a r (x) = E [Z] = \sum_{z} z p_{Z} (z) = 0 \cdot \frac{1}{9} + 1 \cdot \frac{2}{9} + 4 \cdot \frac{2}{9} + 9 \cdot \frac{2}{9} + 16 \cdot \frac{2}{9} = \frac{60}{9}

מסתבר, שיש דרך קלה יותר לחשב את ה שונות של $X$ על ידי שימוש בפונקציית מסת ההסתברות של $X$ בלי שיש צורך לחשב את פונקציית מסת ההסתברות של $(X - E [X])^{2}$ . השיטה הזאת מבוססת על החוק הבא:

E [g (X)] = \sum_{x} g (x) \cdot p_{X} (x)

כדי להוכיח את זה נשים לב שמתקיים עבור $Y = g (x)$

p_{Y} (y) = \sum_{{x | g (x) = y}} p_{X} (x)

כלומר לוקחים את כל האיברים ב $X$ שהפעלת $g$ עליהם ייתן $y$ וסוכמים את ההתסברויות שלהם זה מסתדר גם אינטואיטיבית שכן אנחנו לוקחים פשוט איברים מ $X$ ועושים עליהם שינוי כלשהו הגיוני שכל האיברים יהיו שייכים לתמונה ההפוכה של $Y$ .
Pasted image 20221125105939.png|350

סך הכל יתקיים

\begin{matrix} E [g (X)] = E [Y] = \\ \sum_{y} y p_{Y} (y) = \sum_{y} y \sum_{{x | g (x) = y}} p_{X} (x) \\ = \sum_{y} \sum_{{x | g (x) = y}} y p_{X} (x) \\ = \sum_{y} \sum_{{x | g (x) = y}} g (x) p_{X} (x) \\ = \sum_{x} g (x) p_{X} (x) \end{matrix}

לפיכך אם נציב את הנ״ל בשונות של $X$ נקבל

v a r (X) = E [(X - E [X])^{2}] = \sum_{x} (x - E [x])^{2} p_{X} (x)

באופן דומה ה מומנט ה $n$ -י ניתן על ידי

E [X^{n}] = \sum_{x} x^{n} p_{X} (x)

וכך אין צורך לחשב את פונקציית מסת ההסתברות של $X^{n}$ .

אז כמו שניתן לראות , השונות היא תמיד אי שלילית, נשאלת השאלה מתי היא $0$ ? מהגדרת הסכום אנחנו יודעים שסכום של מספרים אי שליליים הוא 0 אמ״מ כל אחד מהגורמים הוא $0$ והמצב הזה יתרחש רק כאשר $x = E [X]$ ואז המשתנה לא באמת ״רנדומי״ . הערכים שלו שווים לתוחלת ופונקצייה מסת ההסתברות תחזיר $1$ לכל ערך.

תכונות חשובות של תוחלת ושונות

ליניאריות התוחלת: נשתמש בחוק התוחלת של פונקציה שהוכחנו למעלה כדי לפתח כמה תכונות חשובות מאוד של התוחלת והשונות. נתחיל ממשתנה רנדומי $Y$ שמוגדר באופן הבא

Y = a X + b

כאשר $a, b$ הם סקלרים כלומר $Y$ הוא פונקצייה ליניארית על $X$ , יתקיים:

E [Y] = \sum_{x} (a x + b) p_{X} (x) = a \sum_{x} x p_{X} (x) + b \sum_{x} p_{X} (x) = a E [X] + b

מסקנה מליניאריות התוחלת על השונות

\begin{matrix} v a r (Y) = \sum_{x} (a x + b - E [a X + b])^{2} p_{X} (x) \\ = \sum_{x} (a x + b - a E [X] - b)^{2} p_{X} (x) \\ = a^{2} \sum_{x} (x - E [X])^{2} p_{X} (x) = a^{2} v a r (X) \end{matrix}

אם כן נקבל שתי מסקנות חשובות

v a r [X + b] = v a r [X]

v a r [a X] = a^{2} v a r [X]

נסתכל על דרך נוספת לחישוב השונות של משתנה רנדומי $X$

v a r (X) = E [X^{2}] - (E [X])^{2}

ההוכחה לכך פשוטה:

\begin{matrix} v a r (X) = \sum_{x} (x - E [X])^{2} p_{X} (x) \\ = \sum_{x} (x^{2} - 2 x E [X] + (E [X])^{2}) p_{X} (x) \\ = \sum_{x} x^{2} p_{X} (x) - 2 E [X] \sum_{x} x p_{X} (x) + (E [X])^{2} \sum_{x} p_{X} (x) \\ = E [X^{2}] - 2 (E [X])^{2} + (E [X])^{2} = \\ E [X^{2}] - (E [X])^{2} \end{matrix}

המעבר השלישי נובע מהוצאת סקלר של הסכום $\sum_{x} 2 x E [X] p_{X} (x)$

נשים לב שאם פונקצייה $g$ אינה ליניארית, אין בהכרח מתקיים ש $E [g (X)] = g (E [x])$ וההוכחה למעלה היא הסבר מצויין ללמה זה לא תמיד נכון אחרת השונות תמיד הייתה 0 .

$X \geq 0 \to E [X] \geq 0$
עבור $c$ קבוע יתקיים $E [c] = c$

תוחלת ושונות של משתנים רנדומים נפוצים

תוחלת ושונות של ברנולי

נזכיר שפונקציית מסת ההסתברות של ברנולי נראת כך

p_{X} (k) = {\begin{cases} p & k = 1 \\ 1 - p & k = 0 \end{cases}

כלומר יתקיים ש

E [X] = 1 \cdot p + 0 \cdot (1 - p) = p

כמו כן

E [X^{2}] = 1^{2} \cdot p + 0 (1 - p) = p

ולכן

v a r (X) = E [X^{2}] - (E [X])^{2} = p - p^{2} = p (1 - p)

תוחלת ושונות של משתנה אחיד

נדגים את זה על הטלה של קובייה הוגנת. ה $P M F$ ייראה כך

p_{X} (k) = {\begin{cases} \frac{1}{6} & k \in [1, 6] \\ 0 & e l s e \end{cases}

פונקציית מסת ההתסתברות סימטרית סביב $3.5$ ולכן זה התוחלת ועבור ה שונות נקבל בהצבה פשוטה לפי הגדרה את התשובה.
סך הכל באופן כללי
ִ Pasted image 20221126002954.png|400
ה $P M F$ של משתנה רנדומי אחיד בקטע $[a, b]$ כך שההתסברות של כל תוצאה היא $\frac{1}{b - a + 1}$ יקיים ש

E [X] = \frac{a + b}{2}, v a r (X) = \frac{(b - a) (b - a + 2)}{12}

נשים לב שפונקציית מסת ההסתברות תיראה ככה

p_{X} (k) = {\begin{cases} \frac{1}{b - a + 1} & k \in [a, b] \\ 0 & e l s e \end{cases}

תוחלת ושונות של משתנה פואסון

נזכיר שפונקציית מסת ההסתברות של פואסון היא

p_{X} (k) = e^{- λ} \frac{λ^{k}}{k!}

עבור התוחלת נקבל

\begin{matrix} E [X] = \sum_{k = 0}^{\infty} k e^{- λ} \frac{λ^{k}}{k!} = \sum_{k = 1}^{\infty} e^{- λ} \frac{λ^{k}}{(k - 1)!} = λ \sum_{k = 1}^{\infty} e^{- λ} \frac{λ^{k - 1}}{(k - 1)!} \\ \underset{m = k - 1}{=} λ \sum_{m = 0}^{\infty} e^{- λ} \frac{λ^{m}}{m!} = λ \end{matrix}

המעבר האחרון נובע בגלל ש

\sum_{m = 0}^{\infty} e^{- λ} \frac{λ^{m}}{m!} = \sum_{m = 0}^{\infty} p_{X} (m) = 1

זאת תכונת הנרמלות של פונקציית מסת ההסתברות. חישוב דומה יראה שגם השונות של משתנה פואסון היא $λ$ אבל זה בהרחבה ב שונות של משתנה פואסון

תוחלת ושונות של משתנה בינומי

התוחלת של משתנה בינומי
השונות של משתנה בינומי

תוחלת ושונות של משתנה גיאומטרי

קבלת החלטות על ידי שימוש בתוחלת

נסתכל על בעיה הסתברותית בשם the quiz problem . בהינתן משחק חידות שבו בן אדם מקבל שתי שאלות וחייב להחליט לאיזה שאלה הוא יענה ראשון. (הבחירה היא לא מקרית).
שאלה 1 תיענה נכונה בהסתברות של $0.8$ והעונה נכונה יקבל פרס בשווי $100$ דולר.
שאלה 2 תיענה נכונה בהסתברות $0.5$ והעונה נכונה יקבל פרס של $200$ דולר.
אם השאלה הראשונה שנבחר נענית לא נכונה , המתמודד לא יכול להמשיך לשאלה השנייה. אם השאלה הראשונה נענתה נכונה, המתמודד יכול ללכת לשאלה השנייה.

השאלה המתבקשת היא, איזה מהשאלות עלינו לענות ראשונה על מנת למקסם את הרווח שלנו.
השאלה לא כל כך אינטואיטיבית בגלל ההשלכות של בחירת השאלה , במידה ואטעה לא אוכל להמשיך.
כדי לענות על השאלה ששאלנו, נסמן את הפרס הכולל שנזכה בו כשמשתנה רנדומי $X$ . ונרצה לחשב את התוחלת $E [X]$ תחת שתי הבחירות לאיזה שאלה נענה קודם.

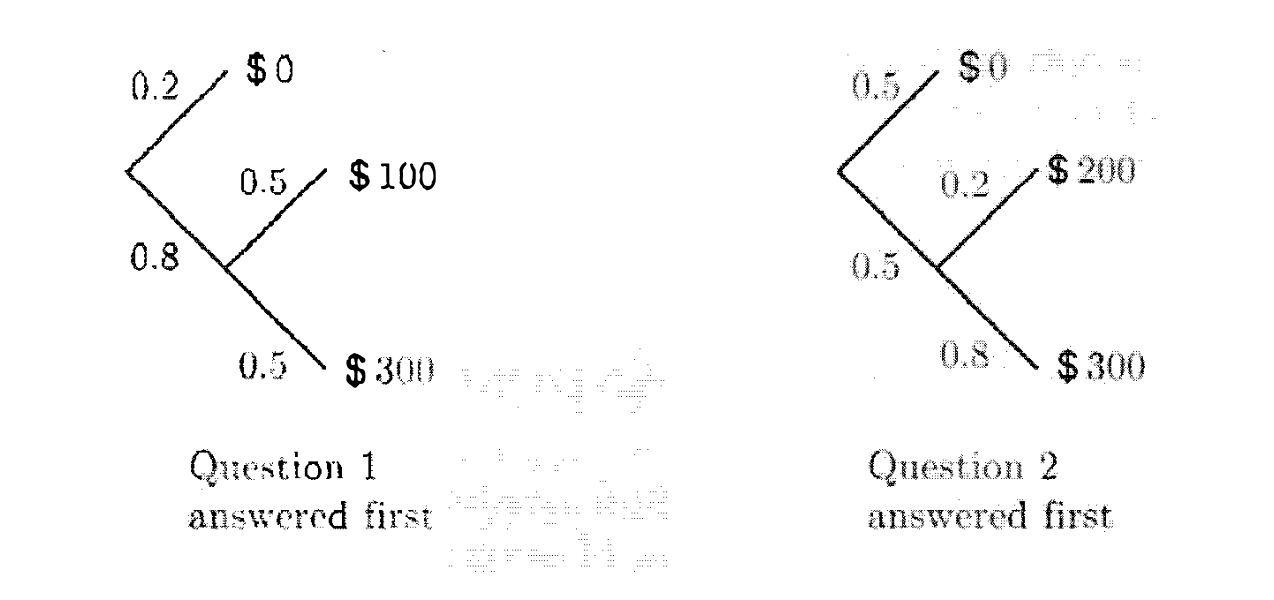
Pasted image 20221205204620.png|450

א) נענה על שאלה אחת קודם, במצב זה ה PMF של X יהיה

\begin{matrix} p_{x} (0) = 0.2 \\ p_{x} (100) = 0.8 \cdot 0.5 \\ p_{x} (300) = 0.5 \cdot 0.8 \end{matrix}

במצב זה התוחלת תצא $E [X] = 160$ .

ב) נענה על שאלה שתיים קודם, במצב זה ה PMF של X יהיה

\begin{matrix} p_{x} (0) = 0.5 \\ p_{x} (200) = 0.2 \cdot 0.5 \\ p_{x} (300) = 0.5 \cdot 0.8 \end{matrix}

ובמצב זה התוחלת תהיה $E [X] = 140$
אם כן, נראה כי בחירה של השאלה הראשונה עדיפה שכן התוחלת או מרכז המסה של הסכומים שבהם נזכה יהיה יותר גדול.

נוכל להכליל את המסקנות מהתרגיל הזה באופן הבא:
בהנתן $p_{1}, p_{2}$ ההסתברויות לענות נכונה על שאלות $1, 2$ בהתאמה, ונסמן $v_{1}, v_{2}$ את הפרסמים המתקבלים מזכייה.
אם שאלה אחת נענית קודם נקבל

E [X] = p_{1} (1 - p_{2}) v_{1} + p_{1} p_{2} (v_{1} + v_{2}) = p_{1} v_{1} + p_{1} p_{2} v_{2}

אם השאלה השנייה נענית ראשונה נקבל

E [X] = p_{2} (1 - p_{1}) v_{2} + p_{2} p_{1} (v_{2} + v_{1}) = p_{2} v_{2} + p_{2} p_{1} v_{1}

כלומר נקבל סך הכל שבחירה של שאלה אחת היא אופטימלית אם ורק אם

\frac{p_{1} v_{1}}{1 - p_{1}} \geq \frac{p_{2} v_{2}}{1 - p_{2}}

כלומר הבחירה האופטימלית היא סידור השאלות בסדר יורד של הביטוי הזה. (ניתן להכליל את זה אף יותר למקרה של $n$ שאלות אבל באופן כללי עדיין נקבל שהאופטימלי הוא הביטוי הנ״ל בעל הערך הגבוה ביותר).