#probability #computer_science

משתנים רנדומיים - רציף

PDF

משתנה רנדומי $X$ ייקרא רציף אם ישנה פונקצייה אי שלילית $f_{X}$ , נסמנה $P D F = probability density function$ של $X$ (פונקציית צפיפות ההסתברות) כך ש:

P (X \in B) = \int_{B} f_{X} (x) d x

כאשר $B$ היא תת קבוצה של $R$ או של מרחב מדגם שעוצמתו היא עוצמת הממשיים כלומר real axis.
באופן ספציפי, נאמר שההסתברות של ערך כלשהו ב $X$ להיות בטווח ערכים מסויים הוא

P (a \leq X \leq b) = \int_{a}^{b} f_{X} (x) d x

הבחנה

נשים לב שמההגדרה הנ״ל נוכל לראות כי

P (a \leq X \leq b) = P (X \leq b) - P (X \geq a)

Info

נזכיר שעוד במודלים הסתברותיים אמרנו שחוק הסתברות תקין במקרה רציף היא הסתברות=שטח, וכעת חוזרים לזה
במילים פשוטות אם ישנה פונקצייה שהאינטגרל הכלוא שלה מתאר את ההסתברות של ערך להיות בשטח הכלוא אז המשתנה הזה רציף.

מהגדרת האינטגרל אנחנו יכולים להסיק שהמשמעות היא שההסתברות הינה השטח שמתחת לגרף. וגם נוכל להסיק שמרחבים רציפים ההסתברות לקבל ערך בודד הינה $0$ כיוון ש לכל $a$ יתקיים $P (X = a) = \int_{a}^{a} f_{X} (x) d x = 0$
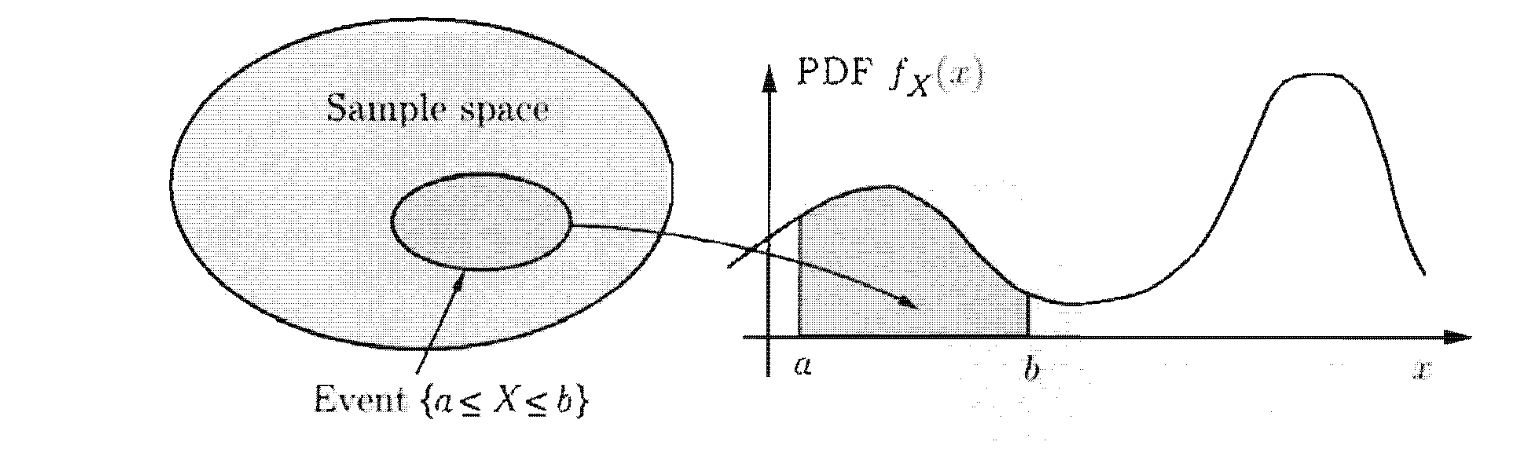
Pasted image 20221216184800.png|500
מהסיבה הזאת יתקיים שהוספה או הורדה של נקודות מקצוות התחום לא תשפיע על ההסתברות

P (a \leq X \leq b) = P (a < X < b) = P (a \leq X < b) = P (a < X \leq b)

התכונות ש $f_{X}$ צריכה לקיים כדי להיות $P D F$ תקין הן:

$f_{X} (x) \geq 0$ כלומר פונקצייה אי שלילית לכל ערכיה
נורמליזציה בדומה ל PMF הסכום של כל ערכי התמונה האפשריים צריך להיות $1$

\int_{\pm \infty} f_{X} (x) d x = P (- \infty < X < \infty) = 1

באופן גרפי זה אומר שכל השטח שמתחת לגרף צריך לשאוף ל $1$ .

כדי לקבל אינטואיצייה על PDF, נשים לב שעבור הקטע $[x, x + δ]$ עם $δ$ קטנה מאוד נקבל

P ([x, x + δ]) = \int_{x}^{x + δ} f_{X} (t) d t ≃ f_{X} (x) \cdot δ

זה נובע מהגדרת האינטגרל המסויים לפי דרבו שמגדירה אינטגרל כסדרה של סכום שטחי המלבנים (בגלל זה ניתן להתייחס לסכום כאינטגרל ולאינטגרל כסכום בהמון מצבים).
אם כן $f_{X} (x)$ היא מעין ״מסת הסתברות עבור יחידת אורך״ בקרבת $x$ .
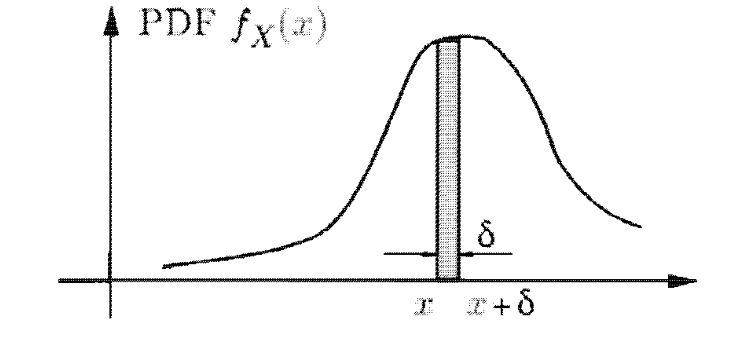
Pasted image 20221216192313.png|550
נשים לב שה PDF משמשת אותנו לחישוב הסתברויות אבל $f_{X} (x)$ היא לאו דווקא הסתברות של מאורע כלשהו .

משתנה רנדומי אחיד רציף

נניח שישנו מהמר שמסובב גלגל מזלות עם ערכים בין $0$ ל $1$ והוא עוקב אחר התוצאות שיוצאות. נניח שלכל תתי הקטעים של $[0, 1]$ שהם באותו האורך יש הסתברות שווה, אם כן, נוכל למדל את הניסוי הזה עם משתנה רנדומי $X$ באופן הבא:

P D F = f_{X} (x) = {\begin{cases} c & x \in [0, 1] \\ 0 & e l s e \end{cases}

כאשר $c$ הוא קבוע כלשהו. כלומר הערך הוא קבוע בקטע הזה. אם כן נרצה לבדוק שהפונקצייה שהגדרנו אכן תקינה כ $P D F$ ומקיימת את תכונת הנורמליזציה

1 = \int_{- \infty}^{\infty} f_{X} (x) d x = \int_{0}^{1} c d x = c \int_{0}^{1} d x = c

כלומר השטח של הפונקצייה בקטע $[0, 1]$ הוא 1 כי מסביב לקטע הזה הערך של הפונקצייה הוא $0$ ולכן זאת פונקציית צפיפות תקינה.
אם כן נוכל באופן דומה לחלץ את $c$ עבור כל תת מקטע $[a, b]$ שנבחר :

f_{X} (x) = {\begin{cases} \frac{1}{b - a} & x \in [a, b] \\ 0 & e l s e \end{cases}

באופן הזה נקבל שלכל תתי מקטעים באותו אורך יתקיים שישנו אותו השטח.
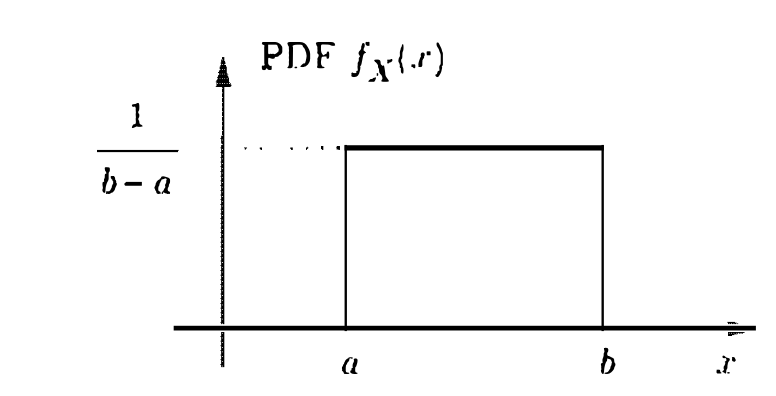
Pasted image 20221216212012.png|550
הערך הנ״ל משמר גם כן את תכונת הנורמליזצייה

\int_{a}^{b} \frac{1}{b - a} d x = \frac{1}{b - a} \int_{a}^{b} d x = \frac{1}{b - a} \cdot (b - a) = 1

PDF קבוע ״בחתיכות״

זמן הנהיגה של סער לעבודה הוא בין $15$ ל $20$ דקות ביום שמשי ובין $20 - 25$ דקות ביום גשום. כל זמני ההגעה הם שווי הסתברות.
נניח שההסתברות ליום שמשי היא $\frac{2}{3}$ וליום גשום היא $\frac{1}{3}$ . מהי פונקציית ה PDF של זמן הנהיגה שנסמנו $X$ .
זמני ההגעה שווים בכל מקרה בנפרד כלומר $X$ הוא קבוע שונה בכל אחד מהמקטעים $[15, 20], [20, 25]$ .
יתרה מכך, שתי המקטעים האלה מכילים את כל זמני הנהיגה האפשריים ולכן פונקציית הPDF תחזיר $0$ לכל ערך שאינו במקטעים הללו.
אם כן נקבל פונקציית צפיפות הסתברות כזאת

f_{X} (x) = {\begin{cases} c_{1} & x \in [15, 25] \\ c_{2} & x \in [20, 25] \\ 0 & e l s e \end{cases}

כאשר $c_{1}, c_{2}$ הם קבועים שאותם נוכל לחלץ מההסתברויות הנתונות לנו על יום גשום ויום שמשי:

\frac{2}{3} = P (sunny day) = \int_{15}^{20} f_{X} (x) d x = \int_{15}^{20} c_{1} d x = 5 c_{1}

אם כן נוסחה דומה תיתן לנו גם את $c_{1}$ ונקבל

c_{1} = \frac{2}{15}, c_{2} = \frac{1}{15}

נשים לב שזה לא מצב של התפלגות אחידה, אלא קבוע בצורה חלקים למשל בגרף עם שלושה קבועים זה ייראה כך
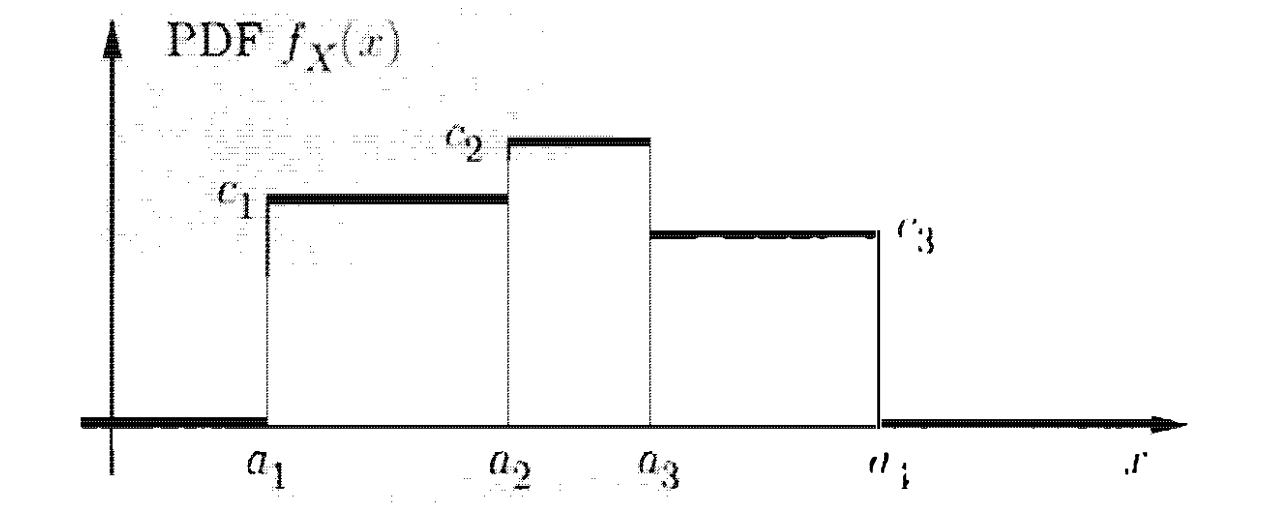
Pasted image 20221218000354.png|550
התפלגות אחידה בקטע דורשת שבקטע הזה תהיה את אותה הסתברות ומסביב הכל $0$ , כך ששטח המלבן הנוצר בקטע הזה יהיה $1$ .
נוכל להכליל את הדוגמה, עבור משתנה רנדומי $X$ שה $P D F$ שלו מכיל מספר מקטעים קבועים $n$ :

f_{X} (x) = {\begin{cases} c_{i} & x \in [a_{i}, a_{i + 1}] \\ 0 & e l s e \end{cases}

כאשר $i = 1, 2, \dots, n - 1$ . נשים לב ש $c_{i}$ יהיו חייבים לקיים את תכונות הנורמליזציה ולכן יש לנו כבר נתון אחד על הסכום של כל המלבנים שגובהם הם הקבועים הללו (סכום כל המלבנים הוא $1$ ).

תוחלת

התוחלת של משתנה רנדומי רציף $X$ מוגדרת כך

E [X] = \int_{- \infty}^{\infty} x f_{X} (x) d x

זה דומה לתוחלת חוץ מהעובדה שפונקציית מסת ההסתברות הוחלפה בפונקציית הצפיפות, והסכימה נעשית על ידי אינטגרל.
המשמעות של התוחלת במקרה הרציף זהה למשמעות במקרה הבדיד שכן זה מעין ״מרכז גרביטציה״ של פונקציית הצפיפות. בסופו של דבר מדובר בגבול של סכום אינסופי של ניסויים חוזרים בלתי תלויים.
אם $X$ הוא משתנה רנדומי רציף עם pdf מוגדר, כל פונקצייה ממשית $Y = g (X)$ היא גם כן משתנה רנדומי. נשים לב ש $Y$ יכול להיות רציף אבל גם יכול להיות בדיד למשל

g (x) {\begin{cases} 1 & x > 0 \\ 0 & e l s e \end{cases}

במצב זה $Y = g (x)$ הוא משתנה רנדומי בדיד שלוקח ערכים מהקבוצה הסופית הבינארית.
בשתי המקרים נקבל שהתוחלת של $g (x)$ מקיימת את כלל התוחלת

E [g (x)] = \int_{- \infty}^{\infty} g (x) f_{X} (x) d x

באופן דומה השונות והמומנט מוגדרים באופן דומה רק במקום סכום משתמשים באינטגרל

m o m e n t (X) = E [X^{n}] = \int_{- \infty}^{\infty} x^{n} f_{X} (x) d x

v a r (X) = E [(X - E [X])^{2}] = \int_{- \infty}^{\infty} (x - E [X])^{2} f_{X} (x) d x

ועבור התוחלת תתקיימנה התכונות שלמדנו מהמקרה הבדיד.

תוחלת ושונות של משתנה אחיד

נחשב את התוחלת של #משתנה רנדומי אחיד רציף שדיברנו עליו

E [X] = \int_{- \infty}^{\infty} x f_{X} (x) d x = \int_{a}^{b} x \cdot \frac{1}{b - a} d x = \frac{1}{b - a} \cdot \frac{1}{2} x^{2} |_{a}^{b} = \frac{1}{b - a} \cdot \frac{b^{2} - a^{2}}{2} = \frac{a + b}{2}

האינטואיצייה שלנו הייתה מחזירה לנו אותו דבר שכן $\frac{a + b}{2}$ זה בידיוק האמצע של המלבן.
כעת נחשב את השונות

\begin{matrix} E [X^{2}] = \int_{a}^{b} \frac{x^{2}}{b - a} d x = \frac{1}{b - a} \int_{a}^{b} x^{2} d x = \frac{1}{b - a} \cdot \frac{1}{3} x^{3} |_{a}^{b} = \frac{b^{3} - a^{3}}{3 (b - a)} = \frac{a^{2} + a b + b^{2}}{3} \end{matrix}

ומכאן השונות תתקבל באופן הבא

v a r (X) = E [X^{2}] - (E [X])^{2} = \frac{a^{2} + a b + b^{2}}{3} - \frac{(a + b)^{2}}{4} = \frac{(b - a)^{2}}{12}

משתנה מקרי מעריכי

משתנה מקרי מעריכי הוא מהצורה

f_{X} (x) = {\begin{cases} λ e^{- λ x} & x \geq 0 \\ 0 & e l s e \end{cases}

כאשר $λ$ הוא פרמטר חיובי שמאפיין את הPDF .

\int_{- \infty}^{\infty} f_{X} (x) d x = \int_{0}^{\infty} λ e^{- λ x} d x = - e^{- λ x} |_{0}^{\infty} = 1

נשים לב שההסתברות של $X$ לעלות על ערך מסויים קטנה באופן מעריכי. עבור $a \geq 0$ נקבל

P (X \geq a) = - e^{- λ x} |_{a}^{\infty} = e^{- λ a}

משתנה מהסוג הזה יכול למדל באופן די טוב את כמות הזמן שלוקחת למאורע כלשהו להתרחש, כמו הודעה שמגיע למחשב, הזמן שייקח למכשיר להשבר, מנורה שנשפרת ועוד...
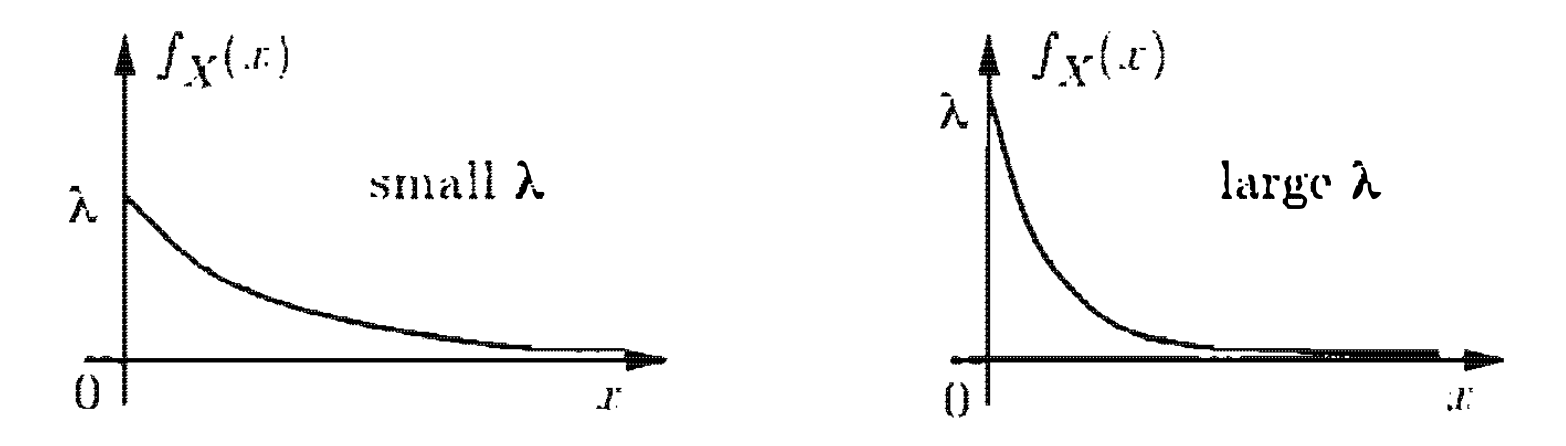
Pasted image 20221218014805.png|350
בCDF נראה שהוא מתקשר למשתנה גיאומטרי שהוא מתקשר ל״זמן בדיד״ כלומר מספר הפעמים עד שאירוע כלשהו מתרחש.

התוחלת והשונות שלו יהיו:

E [X] = \int_{0}^{\infty} x λ e^{- λ x} d x = (- x e^{- λ x}) |_{0}^{\infty} + \int_{0}^{\infty} e^{- λ x} = 0 - \frac{e^{- λ x}}{λ} |_{0}^{\infty} = \frac{1}{λ}

המעבר השמח הזה נובע מאינטגרציה בחלקים
בדומה נקבל

E [X^{2}] = \int_{0}^{\infty} x^{2} λ e^{- λ x} d x = (- x^{2} e^{- λ x}) |_{0}^{\infty} + \int_{0}^{\infty} 2 x e^{- λ x} d x = 0 + \frac{2}{λ} E [X] = \frac{2}{λ^{2}}

ומכאן נוכל לקבל שהשונות היא

v a r (X) = \frac{2}{λ^{2}} - \frac{1}{λ^{2}} = \frac{1}{λ^{2}}

נשים לב שגם משתנה מקרי מערכי הוא חסר זכרון כמו הגיאומטרי כלומר:

f_{X - n | X > n} (k) = f_{X} (k)

מה זה בכלל

λ

המשמעות של $λ$ למעשה זה מעין קבוע דעיכה, כלומר ככל שקבוע הדעיכה גדול יותר ככה התוחלת קטנה יותר כלומר מרכז המסה נמצא בהתחלה והמשמעות של זה היא שההסתברות למאורע גדולה יותר, שזה בעצם אומר שהזמן עד שמאורע יתרחש קצר יותר. באופן דומה אם קבוע הדעיכה קטן יותר ככה התוחלת גדולה יותר (אפשר לראות בתמונה למטה שלוקח זמן עבור הגרף האדום להתקרב ל 0 יותר מהאחרים ולכן מרכז המסה של הפונקצייה יהיה יותר ימינה בציר הx) ולכן ההסתברות שהמאורע יתרחש קטנה יותר כלומר יותר זמן המתנה.
היא מתארת תופעות אקראיות שהסיכוי להתרחשותן קבוע בזמן, כגון התפרקות רדיואקטיבית או הזמן עד לתקלה בנורה או ברכיב חשמלי
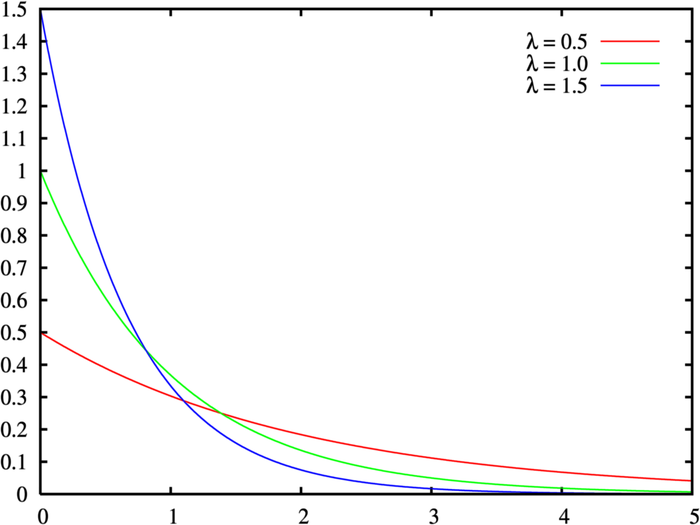
Pasted image 20230126133931.png|300
ההתפלגות המעריכית מתאימה לתיאור הזמן בין אירועים המתרחשים באקראי אך בקצב ממוצע קבוע.
דוגמה מצויינת שמסיברה על ההבדל בין למדה בפואסון ולמדה במעריכי ומה הוא בכלל מייצג