שיערוך שאילתות

לאחר שתיארנו שבסוף שאילתה שכתובה בשפה דיקלרטיבית כמו SQL מתורגמנת ל אלגברה רלציונית נשאלת השאלה כיצר מערכת בסיס הנתונים יודעת לקחת את ה Query plan ולהביא באמצעותה מידע קונקרטי ממאגר הנתונים בצורה יעילה וחכמה.

סימונים:

• $B()$ מייצג את הגודל ב Pages בדיסק.
• $T()$ מספר הרשומות
• $V(.,a)$ מייצג את מספר הערכים הייחודיים שיש בעמודה $a$ של ״.״.
  כאשר ״.״ יכול להיות

$R$ רלציה
$O$ טבלה מפלט של שאילתה
$I$ אינדקס

מימוש פעולת DISTINCT

נרצה להוריד כפילויות מטבלה נתונה.
אם יש מספיק מקום בזכרון ניתן לממש את הפעולה על ידי מבנה נתונים חיפושי כמו טבלת גיבוב. לכל רשומה ב$R$ נכניס אותה לטבלה ונוציא אותה חזרה בפלט של השאילתה אך ורק אם היא לא נמצאת כבר בטבלת ההאש. ברגע שמילאנו page של output, נרשום בחזרה בדיסק.

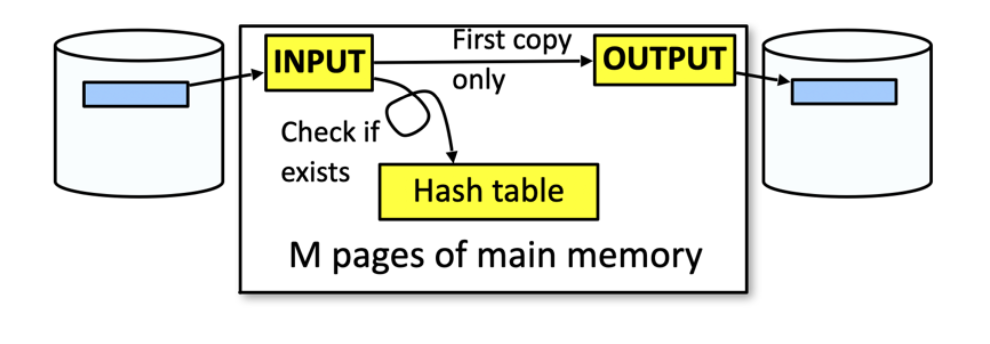
כיוון שאת טבלת הגיבוב מחזיקים בזכרון ולא באחסון חיצוני, אנחנו מבצעים על כל רשומה פעולת קריאה אחת ופעולת כתיבה אחת לכל היותר. וכן העלות היא $2B(R)$ .

במצב שבו אין מספיק זכרון לאחסן טבלת גיבוב אבל כן המידע מאורגן בצורה ממוינת בתוך הזכרון, נוכל פשוט לקרוא את כל המידע מהאחסון ולרשום בחזרה רק את העותק הראשון של כל רשומה. העלות היא זהה.

מימוש פעולת UNION

כל מה שצריך כדי לממש את הפעולה הזאת היא פשוט סריקה מלאה של שתי הטבלאות. אם נרצה לשלב את שתי הטבלאות בלי כפילויות נוכל לבצע full scan ואז distinct.

אם נרצה לממש פעולה הפרש כלומר למצוא רק את מה ששייך לטבלה $A$ ולא ל $B$ נצטרך לחלק למקרים.
אם הזכרון גדול מספיק, נוכל לתחזק טבלת גיבוב כמו מקודם ולהוסיף אליה את טבלה $B$, לאחר מכן לקחת את טבלה $A$ ולחפש אותם בטבלת הגיבוב. אם הם נמצאים שם אז הם גם נמצאים ב $B$ ולכן הם לא מעניינים אותנו כלומר ייחודיים ל $A$ ונוסיף ל output. אם אין מספיק מקום אבל הטבלאות ממוינות, נוכל לעבור עליהם לפי הסדר ולהוסיף רק את האיברים שייחודיים ל $A$ .

מימוש פעולת SELECT

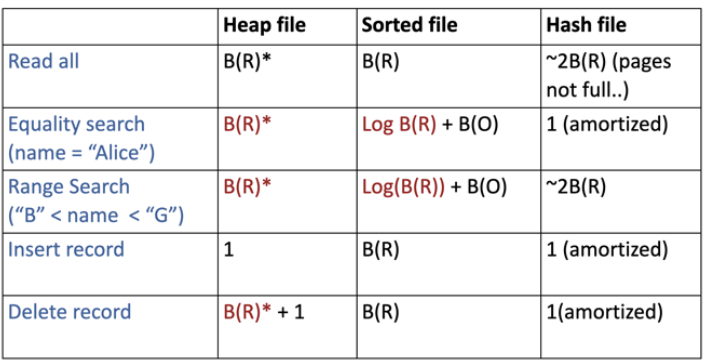
זמני הריצה מצויינים תחת השורה של equality search במידה ואין לנו אינדקסים על בסיס הנתונים. אם יש סידור כלשהו לפי אינדקס בבסיס הנתונים נחלק למקרים.

אם האינדקס הוא clustered אז מספר פעולות הקריאה יהיה $B(O)$ , כמספר הבלוקים שיש ברלציית הפלט של השאילתה כי נוכל ברגע שמצאנו את הרשומה הראשונה באינדקס שעונה על התנאי נוכל להעלות את כל הpage שלה לזכרון ולקרוא.

במידה והאינדקס הוא unclustered הסדר באינדקס לא בהכרח מעיד על הסדר בזכרון ולכן העלות יכולה להיות לכל היותר $T(O)$ כלומר כמספר הרשומות שיש ברלציית הפלט. אם נמנע מהמערכת לעשות קריאות של אותו Page פעמיים נוכל לייעל את הקיראות להיות $min(B(R),T(O))$.

מימוש מכפלה קרטזית

פעולה זאת תבסס את העלויות של פעולות JOIN.
המשמעות של מכפלה קרטזית בין שתי רלציות $R\times S$ היא יצירת רלציה חדשה שמכילה את כל הקומבינציות האפשריות של שתי רשומות מהטבלה.
ניתן לממש זאת פשוט בצורה נאיבית על ידי לולאה מקוננת- עוברים על אובייקט בטבלה $R$ ועבורו עוברים על כל אובייקט בטבלה השנייה. כדי לעשות זאת יש צורך לקרוא את כל הדפים ב $R$ ועל כל דף לקרוא את כל הדפים של $S$ ולכן העלות תהיה

מימוש פעולת JOIN

לאחר שראינו כיצד לממש פעולת מכפלה קרטזית באופן נאיבי, נרצה לנתח את עלות פעולת הjoin.
המימוש ה״נאיבי״ יהיה לבצע לולאה מקוננת ליצרת כל קומבינציה אפשרית בין שתי רשומות מהטבלאות אבל משאירים בסוף רק את הרשומות שמקיימות את תנאי ה JOIN. מימוש זה לא חכם במיוחד שכן אנחנו בונים את כל המכפלה הקרטזית רק בשביל זה.
נממש באופן יותר טוב עם Block Nested Join Loop, ובו במקום לקרוא דף בודד מ$R$ ננסה לקרוא כמה שיותר בבת אחת. טכניקה שראינו כבר במיון.

נניח שיש מספיק מקום ל $M$ דפים בכל איטרציה, נתחזק טבלת HASH שמחזיקה $M-2$ דפים מתוך $R$ במקום לשלוף כל פעם דף ואחריו את כל הדפים מ $S$, לאחר ששלפנו מקבץ זה ואחסנו אותו בטבלת האש ניקח את כל הדפים מ $S$ ונשווה אותם עם טבלת ההאש לצורך מציאת התאמות.

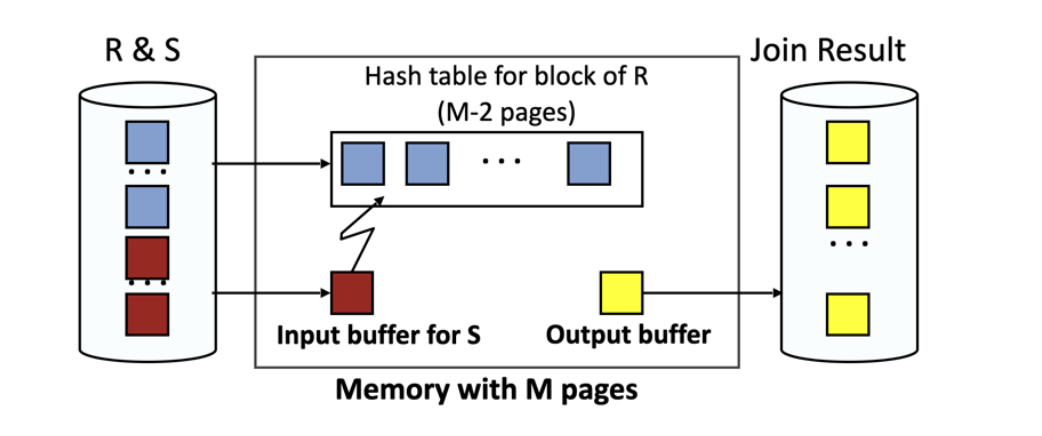
נשים לב שהתיקון הזה צמצם את כמות הקריאות שלוקחים את $S$ עבור כל רשומה $R$ מהזכרון ולכן העלות תהיה

מימוש ל JOIN מבוסס אינדקסים

נניח כי יש לנו אינדקס על העמודה $B$ בטבלה $S$. ונגדיר את הjoin להיות

כלומר שמירת הרשומות בטבלאות המקיימות שיוויון בין העמודות $A,B$ .
באופן מסויים נוכל להסתכל על זה בצורה הנאיבית של שילוב של שתי שאילתות, כלומר נבצע מכפלה קרטזית ואז SELECT. כלומר, עבור כל דף ב$R$ נמצא מתוך $S$ את הרשומות שהערך שלהם בשדה $B$ זהה לערך כלשהו בשדה $A$ ברשומה של $R$, ואת החיפוש נעשה באופן מהיר באמצעות אינדקס. החיפוש באינדקס הוא לא יקר כל כך ונקבל עלות של

כי נצטרך לקרוא את כל הדפים של $R$ פעם אחת ועבור כל רשומה ב $R$ נצטרך לבצע חיפוש של הרשומה מ $S$ עם הערך המשותך בשדה $B$ . מספר קריאות הדפים שנצטרך לבצע מ $S$ הוא $\frac{B(S)}{V(S,B)}$ כאשר נזכור כי $V(S,B)$ זה מספר הערכים הייחודיים שיש בשדה $B$ של טבלה $S$.
הסיבה לכך היא שאם נניח שההתפלגות של מספר ההופעות של הערכים השונים משדה $B$ בטבלה $S$ היא התפלגות אחידה , עבור אותה רשומה ספציפית שאנחנו מתסכלים כעת מ $R$ יתקיים ש רק $\frac{1}{V(S,B)}$ יהיו עם ערך זהה לה בשדה $B$.
מכאן, שמתוך $B(S)$ הדפים הכוללים שיש בטבלה $S$ נצטרך לקרוא רק את החלק הנ״ל מהזכרון לאחר שמצאנו אותו באינדקס וזה יקרה עבור כל רשומה מ $R$ כלומר $T(R)$ פעמים.

Sort-Merge Join

הרעיון מאחורי אלגוריתם זה הוא שאם הרלציות $R,S$ ממוינות לפי העמודות הרלוונטיות, נוכל למצוא התאמות בין שניהם באופן הבא

1. נקרא דף מ $R$ ודף מ $S$
2. נמצא התאמות בין שניהם (שזה יחסית קל בגלל הסדר הממוין)
3. אם הגענו לסוף של $R$ והערך האחרון שם קטן לפי יחס הסדר מהערך שאנחנו עליו ב $S$ , נקרא דף נוסף מ $R$ , אחרת נקרא דף נוסף מ $S$.
4. נמשיך ככה עד שנסיים גם את $R$ וגם את $S$.

נוכל למיין על ידי שימוש ב Merge Sort והעלות של שלב המיון של כל רלצייה יהיה $2B(R)\cdot k$ כאשר $k$ הוא מספר הPasses שאנחנו משתמשים בהם באלגוריתם כלומר כמות הפעמים שמבצעים מיזוג.

העלות על חיפוש הערכים בין שתי הטבלאות תהיה כעלות של מעבר על שתי רלציות בשלמותן $B(R)+B(S)$ ועל כן עלות האלגוריתם תהיה

Hash Join

ניקח את כל הטבלה $R$ ואת כל הטבלה $S$ ונפעיל עליהן את אותה פונקציית גיבוב $h$. כעת נקבל מיפוי של כל הרשומות מ $R$ וכל הרשומות מ $S$ לערכי גיבוב מסוימים. נסמן $R_i,S_i$ את כל הערכים משתי הטבלאות שממופעים לאינדקס ה $i$ בטבלת הגיבוב. כל אחד מהם יהווה חלוקה של $R$. נשמור את המיפוי בדיסק וכעת נדע כל רשומה לאיזה תא בטבלת ההאש הוא שייך.

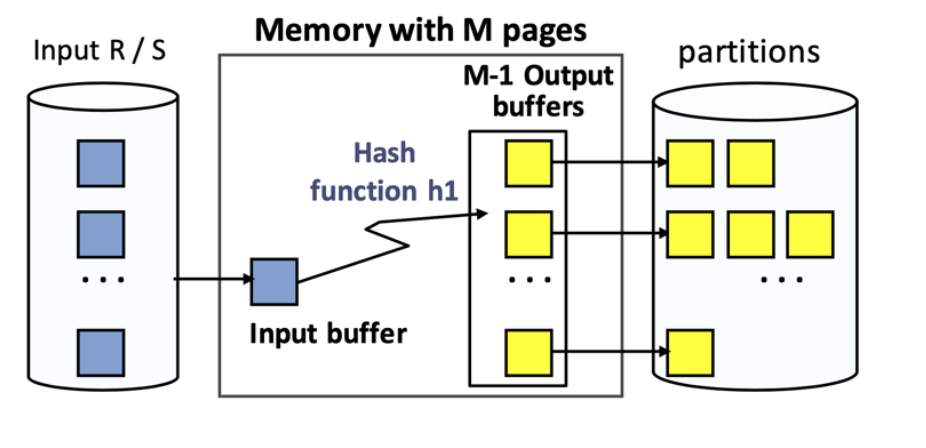
כעת אנחנו יודעים עבור כל טאפל לאיזה תא הוא שייך בטבלת ההאש. על כל חלוקה $R_i$ נמשוך מטבלה $S$ את הרשומות מ $S_i$ בזה אחר זה ונמצא את השוויונות בינהם ואותן נכתוב כתשובה לשאילתה.

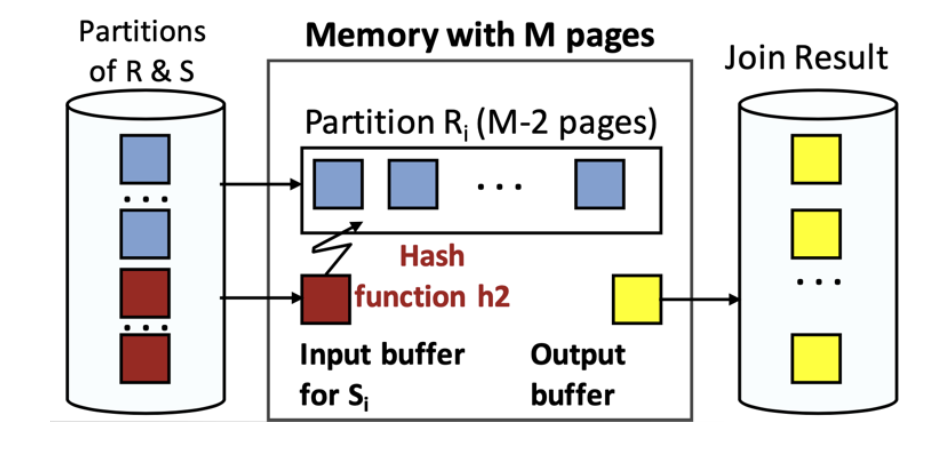
העלות של אלגוריתם היא
א) קריאת של שתי הטבלאות כדי להפעיל עליהן hash.
ב) כתיבת כל המיפויים לזכרון
ג) הוצאת כל קבוצה בחלוקה שזה וכתיבה שזה סך הכל שקול לשתי השלבים הנ״ל

כלומר סך הכל כתבנו את $R,S$ שלוש פעמים לזכרון והעלות היא

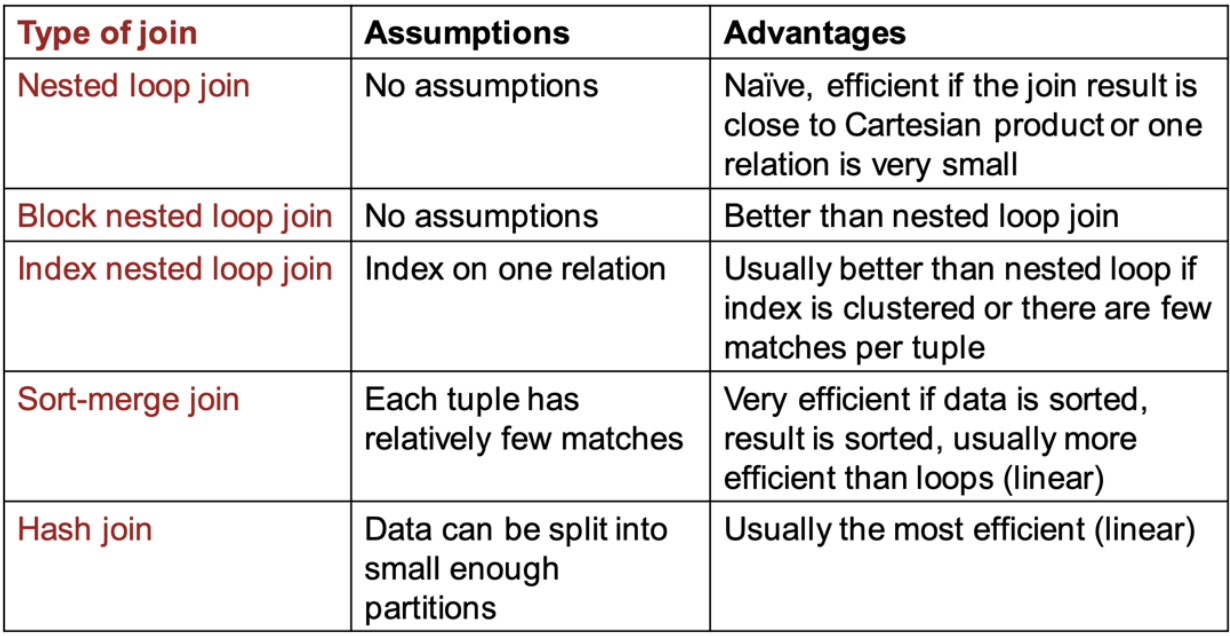
לסיכום: האלגוריתמים של join