מבני נתונים ליניאריים

שמירת מידע וניהולו

לפעמים כמתכנתים נרצה יכולות מתקדמות לשמירה וניהול המידע איתו נרצה לבצע כל מיני פעולות , כאן נכנסים לתמונה מבני הנתונים שהם הנושא של הקורס הזה. כשמדברים ניהול מידע באוסף אנחנו מדברים על ניהול של יישות הנקראת record שהיא יכולה להכיל מספר רב של שדות (למשל סטודנט : שם, שם משפחה , מזהה , כתובת , תחום לימוד , ציונים וכו....). נרצה יכולת לנהל את הrecords בצורה שמתאימה לתוכנית שלנו בצורה היעילה ביותר. אין באמת תשובה נכונה לאיזה מבנה נתונים צריך להשתמש כי כל תוכנית וצרכיה שלה. לכל מבנה יהיו היתרונות והחסרונות שלו וצריך לבחור אותו בהתאם לשאילתות שנרצה לבצע על המידע.

רשימה

אחד הפתרונות המוכרים ביותר היא לעבור עם  sequential allocation
שמאפשר לשמור את המידע בזכרון בסדר מסויים של הכתובות ובקפיצה לפי גודל הrecord שאותו אנחנו שומרים (למשל רשימה בגודל 10 של מספרים שהאיבר הראשון שמור בכתובת 0, גודל כל מספר הוא 4 בייטים ולכן האיבר האחרון יהיה בכתובת 40).
היכולת הזאת טובה מאוד להכנסות והוצאות של איברים אך גרועה לחיפוש . הפתרון שמירה של האוסף בצורה ממויינת ומיון על ידי binary search.

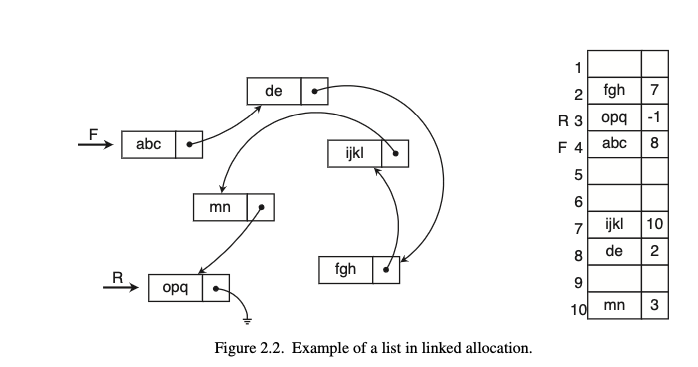
רשימה מקושרת

אחת הבעיות של רשימה היא החסרון שלה בעדכון איברים , כיוון שהרבה פעמים נרצה להכניס איברים תוך כדי שמירה על יחס הסדר המוגדר בין ה records יכולה להיווצר בעיה בשימוש בהקצאה רציפה כיוון שהדבר ידרוש מאיתנו לשנות ולהזיז את האיברים בישביל לפנות מקום לאיבר שנרצה להכניסץ נוכל לפתור את הבעיה הזאת על ידי שימוש ב linked allocation , שזה בעצם אומר שנוכל להקצות מקומות שהם לא בהכרח בסדר רציף, באופן זה נוכל ליצור רשימה מקושרת שמחוברת על ידי מצביעים לכתובות האלו וכשנרצה להכניס כתובת חדשה זה יהיה מאוד פשוט. הבעיה כעת היא שחיפוש הוא לא כזה פשוט יותר כמו ברשימה רגילה שבה כאשר האוסף ממויין נוכל לבצע חיפוש בינארי יעיל לפי אינדקסי החציון. עכשיו , גם אם האוסף ממויין לגשת לאיבר באינדקס כלשהו לוקח $O(n)$ פעולות. נלמד מבני נתונים שעוזרים לנו להתמודד עם הבעיות האלו בהמשך .

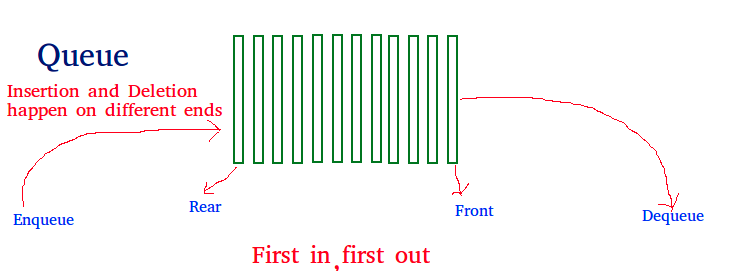
תור

אחד הדרכים היותר טבעיות לארגן את המידע בסדר מסויים הנקרא תור (queue). התור מאפשר לשמור את הנתונים לפי סדר הכנסתם על מנת להוציאם אותו הסדר (FIFO-first in first out). לתור יש את היכולת להכניס איברים לתחילתו ולהוציא מסופו באופן מיידי שלא כולל סריקה, עושים זאת על ידי החזקת שני מצביעים לקידמת התור ולסופו. ניתן לשמור את האיברים ברשימה מקושרת או בהקצאה רציפה כאשר השימוש בהקצאה רציפה דורש מאיתנו לדעת בערך את מספר האיברים איתם נרצה להתעסק אחרת קיים הסיכון ל overflow.

פעולות ההכנסה וההוצאה נקראות enqueue ו dequeue .

מימושים לתור :

• מערך

struct Queue {
	int front, rear, capacity;
	int* queue;
	
	Queue(int c)
	{
		front = rear = 0;
		capacity = c;
		queue = new int;
	}

	~Queue() { delete[] queue; }

	// function to insert an element
	// at the rear of the queue
	void queueEnqueue(int data)
	{
		// check queue is full or not
		if (capacity == rear) {
			return;
		}

		// insert element at the rear
		else {
			queue[rear] = data;
			rear++;
		}
		return;
	}

	// function to delete an element
	// from the front of the queue
	void queueDequeue()
	{
		// if queue is empty
		if (front == rear) {
			printf("\nQueue is empty\n");
			return;
		}

		// shift all the elements from index 2 till rear
		// to the left by one
		else {
			for (int i = 0; i < rear - 1; i++) {
				queue[i] = queue[i + 1];
			}

			// decrement rear
			rear--;
		}
		return;
	}

נבין מה קורה פה - כמו שאמרנו כשעובדים עם מערך צריך שיהיה capacity כל שהוא (מומלץ לפחות) מתודת ההכנסה היא די פשוטה ולוקחת $O(1)$ בהינתן שלא חרגנו מה מכנסה. מתודת ההוצאה דורשת ההעתקה של כל האיברים אחורה וההקטנה איבר ה rear ב1 ולכן זה חסום ב$O(n)$ .

• רשימה מקושרת

struct QNode {
	int data;
	QNode* next;
	QNode(int d)
	{
		data = d;
		next = NULL;
	}
};

struct Queue {
	QNode *front, *rear;
	Queue()
	{
		front = rear = NULL;
	}

	void enQueue(int x)
	{

		// Create a new LL node
		QNode* temp = new QNode(x);

		// If queue is empty, then
		// new node is front and rear both
		if (rear == NULL) {
			front = rear = temp;
			return;
		}

		// Add the new node at
		// the end of queue and change rear
		rear->next = temp;
		rear = temp;
	}

	// Function to remove
	// a key from given queue q
	void deQueue()
	{
		// If queue is empty, return NULL.
		if (front == NULL)
			return;

		// Store previous front and
		// move front one node ahead
		QNode* temp = front;
		front = front->next;

		// If front becomes NULL, then
		// change rear also as NULL
		if (front == NULL)
			rear = NULL;

		delete (temp);
	}
};

שיטה זאת היא העדיפה כמובן כיוון שבמקרה זה אנחנו לא צריכים להעתיק שום דבר בהסרה והוצאה מהתור ולכן כל הפעולות הן ב $O(1)$ .

דוגמאות לשימוש בתור - optimal prefix code

prefix code זה איזשהו פרמטר שניתן לתת לאובייקט בישביל לזהות אותו בצורה יותר מהירה.
נניח שיש קבוצה של מספרים בעלת עוצמה $n$ , נסמנן $a_i:i\in [n]$ . נרצה באופן מתמשך להוריד את שני האיברים הקטנים ביותר מהסדרה ולהוסיף את סכומם כאיבר חדש בקבוצה , כך עד שיישאר איבר אחד, זהו חלק מפתרון של מציאת ה optimal prefix code (לא נגע בפתרון כולו) לפרמטר כלשהו. ברור לנו שאם הקבוצה לא ממויינת נצטרך $n^2$ השוואות.
נוכל למיין ב $nlogn$ ואז לשמור ברישמה מקושרת מה שיאפשר הוצאה , סכימה והכנסה מחדש בזמן קבוע , ונבצע זאת $n-1$ פעמים ולכן עדיין נהיה חסומים ב $nlogn$ פעולות.

נוכל לבצע את המטלה הזאת בזמן זהה אם נשתמש בשני תורים $Q_1$ $Q_2$ . בראשון נשמור את איברי הקבוצה המקוריים בסדר לא יורד (עולה שווה). את השני נחזיק ריק והוא יכיל רק את האיברים שנוצרים על ידי האלגוריתם כלומר סכום של שני איברים מינימליים מהקבוצה . כעת נחפש את המינימום בשני התורים אך שהפעם לא צריך להסתבך לאן מכניסים את הסכום החדש. פשוט ייכנס למאחורי $Q_2$ . אם המערך ממויין זמן העבודה הוא ליניארי

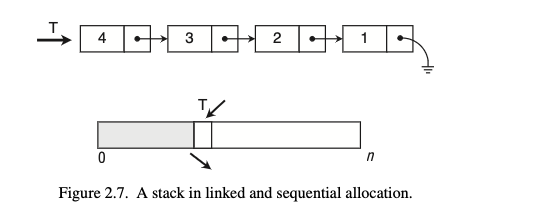
מחסנית

המקבילה של FIFO של המסנית היא LIFO (last in first out). בגלל זה למבנה נתונים קוראים מחסנית, הקליע האחרון שנכניס למחסנית הוא הראשון שיצא בלחיצה על ההדק.

כמו #תור גם מחסנית ניתן לממש על ידי הקצאות רציפות והקצאות מקושרות. בניגוד לתור אנחנו לא מתעסקים עם תחתית המחסנית אלא רק עם מי שנמצא למעלה שהוא ה $top$ . באופן סכמתי זה יראה כך :

כיוון שהמימושים נורא זהים על מערך ורשימה מקושרת ארשום פה רק את הפסודו קוד של כל אחד מהם

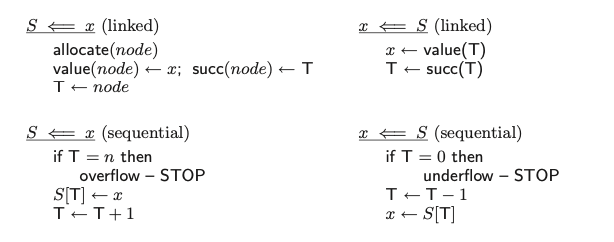
בשני המקרים הוצאה והכנסה היא ב $O(1)$ אבל נורא קשה לבצע פעולות סריקה וכו...

דוגמאות לשימוש במחסנית - ביטויים אריתמטיים

נסתכל על ביטוי מתמטי שאנחנו נתקלנו בו ביסודי

בעוד שהמחשבוני כיס הפשוטים יתרגמו את זה כ35, אנחנו עוד משהיינו ילדים הבנו שיש פה עדיפות לפעולת הכפל לפני פעולת החיבור והתשובה האמיתית היא 19 . ומה אם היה את הביטוי הבא

סגנון הכתיבה הזה כנראה מגיע מסיבות היסטוריות שכן , כיום כשאנחנו מפעילים פונקצייה על משתנה מסויים אנחנו רושמים $f(x)$ ואם זה שני משתנים אז $f(x,y)$ ולא $xfy$ . באופן דומה היינו צריכים לרשום את הביטוי שלנו באופן הבא $add(4,multiply(3,5))$ על מנת שזה יהיה דומה לאופן שבוא רושמים פונקציות.

סגנון הכתיבה הזה נקרא Polish notation .(נקרא גם prefix notation)
בסגנון הכתיבה הזה נרשום את הביטוי באופן הבא

באופן דומה. יש סגנון כתיבה הנקרא Reverse Polish notation. (נקרא גם postfix notation).
בשיטה זאת נרשום קודם את המספרים ולאחר מכן את הביטוי המתמטי שנרצה לבצע. זה יראה כך

הסטנדרט הנ״ל נקרא Infix notation. בשיטה הזאת למחשב יכולה להיות בעיה לדעת מהן סדרי העדיפויות אך בשיטת postfix למעשה הדבר נהיה די פשוט, סך הכל לבצע סריקה של המחסנית תהיה פשוטה מאוד על ידי סריקה של הביטוי עם מחסנית באופן הבא :
מכניסים איברים למחסנית נניח שהשניים האחרונים שנכנסו הם $y,z$ ברגע שייכנס אופרטור $X$ מוציאים את שני האיברים הנ״ל מהמחסנית ומחזירים למחסנית את התוצאה המתקבלת מהפעלת האופרטור על איברים אלו.

בפסודו -

ובאופן ויזואלי על הביטוי

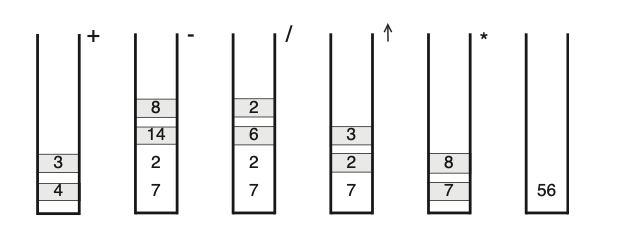
דיברנו על איך להשתמש במחסנית בישביל לחשב בהנחה שהביטוי הגיע בצורת postfix. עם זאת אנחנו יודעים שבפועל אנחנו רושמים ביטוי בצורת infix. נשאלת השאלה איך מתבצעת ההמרה מביטוי אריתמטי רגיל לביטוי בצורת postfix שעליו ניתן לבצע חישובים? לא אפרט כאן את ההסבר אך גם לשימוש הזה משתמשים במחסנית ובטבלת עדיפויות כאשר לסוגריים ניתן העדיפות הכי גבוהה (זה יינתן בצורת מספר) , ולאחר מכן באמצעות הטבלה האופרטים נשמרים במחסנית לפי סדר העדיפויות שלהם.

אנקדוטה המחסנית באה לידי ביטוי גם כאשר אנחנו שומרים זכרון במחשב, בעיקר של משתנים מקומיים שבסוף קריאת הפונקצייה ירדו מהstack. למשל בקריאות ריקורסיביות הפרמטרים נשמרים בstack אחד על השני וכל חזרה אחורה המשתנים המקומיים יורדים מהstack עד שהריקורסיה מסתיימת.

SKIP LIST

רשימה מקושרת לא תומכת בחיפוש בינארי , ורשימה רגילה לא מאפשרת לנו החלפה , הכנסה ומחיקה בצורה מהירה.
נרצה מבנה נתונים שמאפשר לנו לחפש ולהכניס איברים בזמן לוגריתמי לכמות האיברים .

בניית skip list

ניקח את איברי הרשימה המקושרת ונוסיף שני איברים בקצוות איברי sential שנראה שימושים שלהם גם בתרגילים למטה.
נשנה עוד רשימה שתכיל את כל האיברים במקומות הזוגיים עם פוינטר בין האיברים ברשימה הזאת לאיברים ברשימה המקורית

באופן זה נוכל לדלג על איברים בעת חיפוש (במקרה הזה על חצי מהאיברים מדלגים במקרה הגרוע).
נוכל באופן כללי לבנות את המבנה הזה שכל קומה מכילה את האיברים במקומות הזוגית בקומה שמתחתיה עם פוינטרים שמחברים זה ייראה כך

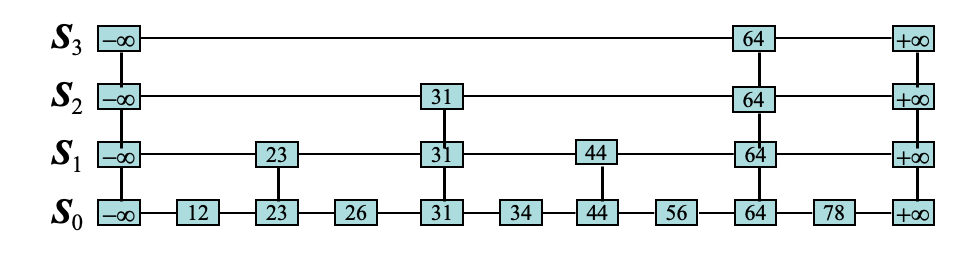
בדומה קצת ל #ערימות ול #עצי AVL כל שכבה אנחנו מקבלים פחות איברים (במבנים הנ״ל זה אומנם הפוך אבל אותו רעיון) ובגלל שכל פעם מעלים רק את המקומות הזוגיים הקומה סך הכל יהיו $logn$ קומות.

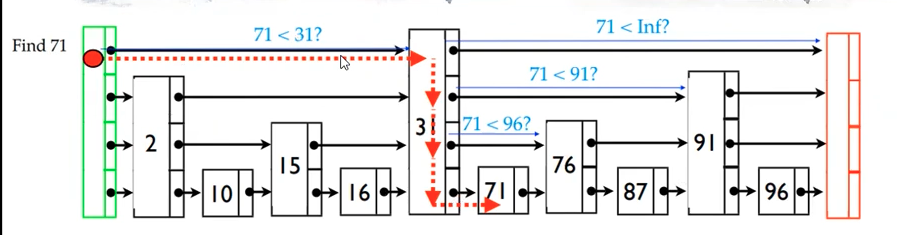
חיפוש

יתחיל מהקומה הגבוהה ביותר ובהתאם לבדיקה האם האיבר גדול יותר או קטן יותר מהאיבר הראשון בקומה נדע על כמה איברים לדלג, ברגע שמצאנו את התחום אפשר לרדת למטה בקומה ולחפש בטווח המצומצם.
הרעיון מאחורי זה הוא מבנה שנותן לנו בערך חיפוש בינארי על כתובות זכרון לא ידועים, בקומה הגבוהה ביותר אני מסנן חצי מהמערך ולאחר מכן רבע ולאחר מכן שמינית וכן הלאה עד להגעה לאיבר הרצוי.

דוגמה לחיפוש 71 בskip list

תמיכה בהכנסות

• נמצא את המיקום שבוא הוא אמור להיות על ידי חיפוש בינארי.
• כל איבר שנכנס יתחיל מהרמה התחתונה, אם הוא נמצא בין שני איברים, הוא מיד עולה למעלה. אם באופן כללי נוצר רצף של שלושה איברים מההכנסה, האיבר האמצעי מבינהם יעלה למעלה.
• זה יחזור על עצמו כל רמה עד הרמה האחרונה שבטוח לא יהיה מצב כזה (אם היה אז פשוט הייתה נוצרת עוד רמה, קצת כמו B-trees שהבנייה נעשת מלמטה למעלה).
  (תמיכה במחיקות היא כבר יותר מסובכת ולא אכנס לזה כאן)

החזרת האיבר ה k בגודלו

נחזיק בכל קודקוד ובכל קומה מידע המעיד על המרחק בינו לבין האיבר הבא באותה קומה אבל המרחק ייצג את הקומה המקורית! , לדוגמה

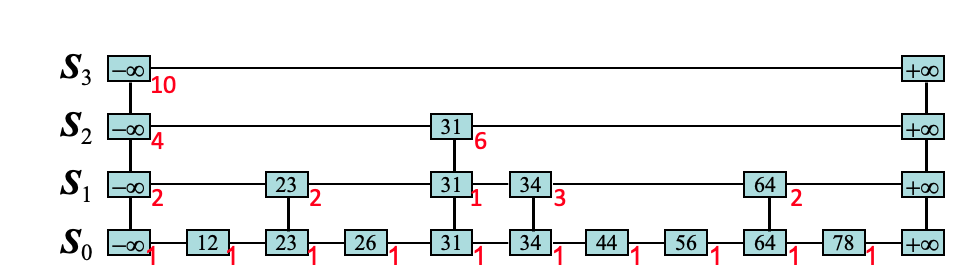
בין 34 ל64 יש 3 איברים ברשימה המקורית.
באופן זה נוכל לדעת האם הדילוג מתאים לנו למציאת $k$ ואם כן נדלג, אחרת נכנס פנימה.