#data_structures #computer_science

Binary Heaps

תורי עדיפות priority queue

אחד ממבני הנתונים הראשונים שדיברנו עליהם בפרק של מבני נתונים ליניאריים היה תור . תור תומך ב $F I F O$ אך הרבה פעמים נרצה לתאר (גם בחיים האמיתיים) מצב שבו הסדר לא בהכרח יהיה לפי סדר הכניסה למבנה אלא לפי נתונים שבאים מתוך ה $r e c o r d$ . למשל בבית חולים אם מצב המטופל חמור הוא ייכנס קודם לחדר הניתוח לפני מישהו ששבר את הרגל גם אם הבחור ששבר את הרגל הגיע לפניו.
מבחינה מתמטית אנחנו מתאים את המבנה הזה עם priority queue. תור עדיפויות הוא מבנה נתונים מופשט כמו מחסנית או תור , כלומר שהוא מייצר איזשהם תכונות שעבורם כל מימוש שניתן עם התוכנות האלה ייקרא ״תור עדיפויות״. בתור עדיפויות כל ערך יחזיק מידע שיתאר את העדיפות שלו באופן מתמטי. כמו כן, נרצה לתמוך בהוצאה והכנסה מהמבנה ושינוי עדיפות בזמן יעיל. כמו כן, נרצה שליפה מהירה לאובייקטים בעדיפות גבוהה.
אחד הפתרונות אולי, יכול להיות מערך ממויין בסדר יורד כך שהעדיפות הגבוהה ביותר נמצאת במקום ה $0$ אבל יהיה לנו בעיה בעדכונים.
פתרון נוסף יכול להיות עץ חיפוש שלוקח $Ω (n l o g n)$ בבנייה אבל עדכונים לוקחים $O (l o g n)$ .

המימוש שאנחנו נתמקד בו בפרק זה נקרא ערימה, והוא סוג מיוחד של עץ בינארי המאפשר לנו לעדכן ב $O (l o g n)$ , לגשת לעדיפות הגבוהה ביותר ב $O (1)$ ובנייה שלו ב $O (n)$ .
השם ערימה נובע מהעובדה שבמבט ראשוני, הכל נראה די מבולגן ולא ברור.
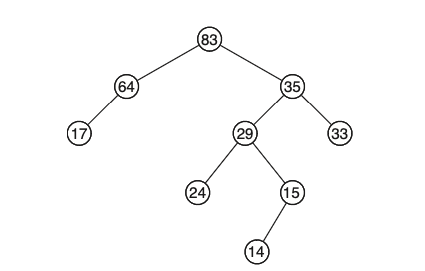
Pasted image 20220627213122.png

אבל ברגע שמבינים את הסדר של הדברים , מקבלים הרבה כוח עליו נדבר מיד.

הגדרת ערימה ועדכוני ערכים

הגדרה ערימה היא עץ בינארי שהערך בכל קודקוד גדול יותר או שווה לזה של ילדיו אם הם קיימים.

מסקנה מיידית מהגדרה זו היא שהערך הגדול ביותר של ערימה תמיד יהיה בשורש שלה, כמו בערימה שלמעלה. מה שכן חשוב לשים לב זה שאין משמעות לסדר בכל קומה בעץ מבחינת ההגדרה הזאת .

אם נרצה למחוק את הערך המקסימלי למשל, נמחק את הערך מהשורש, אבל הפעם אין שום צורך לבדוק כמה ילדים יש או לחפש את האיבר בהדפסת inorder, פשוט מאוד מחליפים את ערך הקודקוד בערך המקסימלי של אחד מילדיו. התהליך הזה מתבצע באופן ריקורסיבי עד להגעה לעלה. אותו נוכל להסיר בלי לדאוג.

אם נרצה להכניס אלמנט חדש אם כן , נרצה להכניס אותו כעלה בזמן $O (1)$ (עלול להדליק לנו כמה נורות אדומות, למשל איך מכניסים עלה ב זמן קבוע לעץ בינארי, נדבר על זה בהמשך). לאחר שמכניסים בזמן קבוע לתחתית הערימה מתחילים סדרה השוואות מלמטה למעלה כדי למצוא את המיקום האמיתי המתאים .

למשל אם נרצה להכניס 52 לערימה מעל (אחרי שמחקנו את 83).
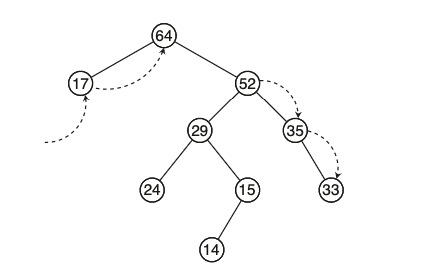
Pasted image 20220627221113.png

כמו בעץ בינארי גם פה פעולות ההכנסה וההוצאה חסומות בגובה העץ, שבמקרים מסויימים יכול להיות $Ω (n)$ . לפיכך, נרצה להוסיף אילוץ על אופן הבנייה שלנו ולהגדיר את הערימה כ עץ בינארי כמעט מלא כמעט שלם. לדוגמא:

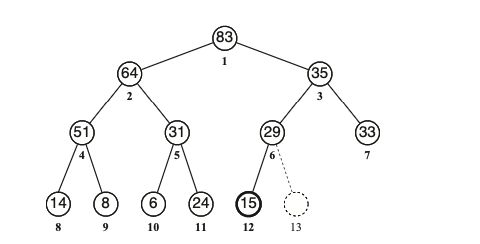
Pasted image 20220627223423.png

ערימה כעץ בינארי כמעט שלם

הכנסה
המטרה של ההגדרה הזאת היא להגביל את חופש התנועה בהחלטה היכן למקם ערך חדש שנכנס. כעת הגבלנו את האופצייה הזאת. כעת אופן ההכנסה של ערכים עדיין יהיה מלמטה למעלה, רק שהפעם את העלה נכניס במטרה למלא את הקומה ה $h$ בעלים, לכן נכניס למקום הראשון משמאל שבו אין עלים בקומה הנמוכה יותר (זה תואר להגדרה שנתנו לעץ בינארי כמעט מלא). נוכל לראות בתמונה למעלה את ההכנסה של 15 ולאן ייכנס האיבר הבא בתור שם. אם נגמר המקום בקומה, ניצור קומה חדשה והאיבר ייכנס כילד שמאלי של הקודקוד השמאלי הנמוך ביותר בערימה.

גם אם הכנסנו ערך שלא מתאים, פשוט נבצע החלפות כמו מקודם.

הוצאה
כדי להדגים מה לעשות בהליך הוצאה נסתכל על הערימה הבאה
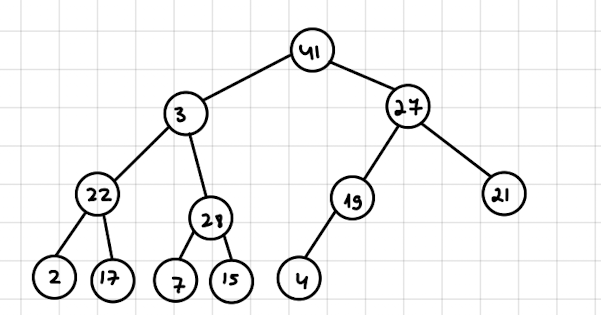
Pasted image 20220627225046.png

לא משנה איזה איבר נרצה להוציא , כל אחד מהם פרט ל $4$ ישבור את מבנה העץ הכמעט מלא. לכן, נגדיר שעבור מחיקה, של קודקוד מסויים , בשלב הראשון של התהליך, נחליף את הערך היחיד שאפשר למחוק, בערך הקודקוד שנרצה להוציא.
למשל , אם נרצה להוציא את 41, נשים את $4$ במקומו. (באופן כללי מחיקה תמיד תתחיל מהאיבר הכי ימני ונמוך בעץ).

השלב השני הוא לבצע כמה תיקונים. נשים לב מה קורה במצב הבא

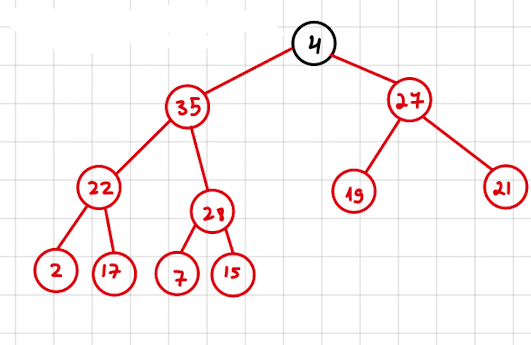
שמנו את $4$ במקום 41 וכעת אין לנו ערימה יותר, עם זאת, נשים לב שכל תתי העצים הם כן ערימה ולפיכך סך הכל נצטרך לפעפע את הערך למטה אם בכלל יש בכך צורך , לכיוון של הילד הגדול יותר מבין השניים ככה עד שנגיע לקודקוד שהילדים שלו יהיו יותר קטנים מ 4 או שנגיע לעלה.

Pasted image 20220627225752.png

כעת הובלנו לכך שגובה העץ יהיה חסום ב logn וכל הפעולות עדיין חסומות בגובה העץ ולכן פעולות ההכנסה וההוצאה יהיו $O (n l o g n)$ .

ערימות מינימום ומקסימום

אומנם דיברתי במונח הכולל של ערימה אבל חשוב לציין שיש שני סוגים של ערימות שנוכל לבנות (את שניהם נבנה בידיוק באותו האופן עם הבדל אחד קטן שתיכף אסביר אותו).

ערימת מקסימום

זאת הערימה שאיתה עבדנו עד כה, ערימה שבה לקודקוד עם ערך מסויים, אם יש ילדים אז הם יותר קטנים מהקודקוד. כל הפעולות הנ״ל אלה הפעולות שדיברנו עליהם למעלה.

ערימת מינימום

הערימה הזאת עובדת אותו הדבר ההבדל היחיד זה שלכל קודקוד עם ערך מסויים , אם יש לו ילדים, אז ערכיהם יותר גדולים ממנו למשל:
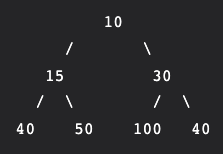
Pasted image 20220627230150.png

ההבדלים בין השניים

שני הבדלים עיקריים , הראשון , ששליפת הערך ב $O (1)$ בערימת מקסימום יהיה הערך עם העדיפות הכי גדולה ובערימת מינימום זה העדיפות הכי קטנה.
ההבדל השני הוא שכל פעולות ההחלפה בערימת מקסימום מבוצעות על יחס הסדר ״גדול או שווה״. בערימת מינימום פעולות ההחלפה יבוצעו בהתאם ליחס הסדר ״קטן שווה״.

מימוש ערימה

עד כה דיברנו על ערימה כעץ בינארי כמעט מלא. אבל גם ציינו שיש כמה נקודות בעייתיות שצריך לעלות. למשל , איך אני מכניס איבר לתחתית העץ ב $O (1)$ או איך אני יכול להסתובב בחופשיות ברחבי העץ מלמטה למעלה כשאנחנו יודעים שבעץ יש רק יכול לרדת למטה.
נוכל לנצל את המגבלה ששמנו על ערימה, כדי לממש את הערימה בלי מצביעים בכלל, אם יש $n$ קודקודים לערימה שלנו נוכל לממש באמצעות מערך בגודל $n$ .

בניית המערך

כמו שאמרנו , עבור $n$ ערכים נבנה (או נקבל כקלט) מערך בגודל $n$ . נתבונן בעץ הבא :
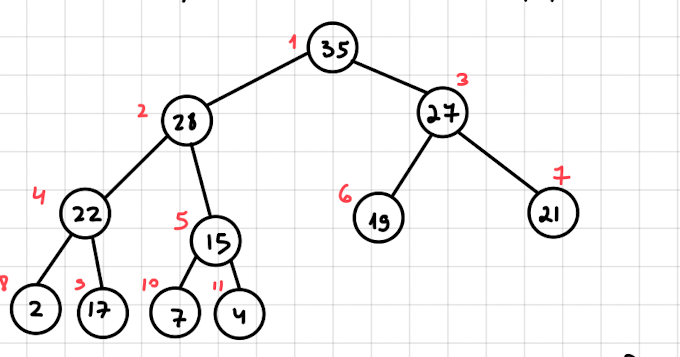
Pasted image 20220628004505.png
האיברים במערך יהיו לפי הקומות משמאל לימין (ככה גם הגדרנו את ה״הירכייה״ בעץ בינארי כמעט מלא). סך הכל המערך יהיה ככה:

Pasted image 20220628004613.png

במינוח מתמטי , לכל $v (i)$ שזה הקודקוד המייצג את האינדקס $i$ במערך יתקיים שהילד השמאלי שלו יהיה באינדקס $2 i$ והילד הימני שלו יהיה באינדקס $2 i + 1$ .

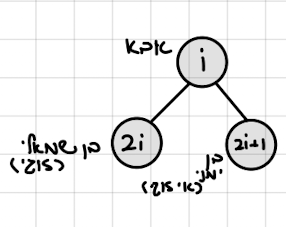
Pasted image 20220628004819.png

כמו כן עבור $v_{j}$ הקודקוד אבא שלו תמיד יהיה $v_{⌊ j / 2 ⌋}$ .
חשוב לשים לב שמהסיבה הזאת האינדקס מתחיל ב1 לכן ניתן לזוז בחופשיות במערך כדי להשיג את הערכים המבוקשים.

המרה של מספר לכפולות של 2

על כל מספר $i$ ניתן להמיר אותו לצורתו הבינארית על ידי האלגוריתם המוכר ממבוא למדעי המחשב (לקחת את השארית עם 2 ולחלק ועד שמגיעים ל0 ובסוף לוקחים את המספר בסדר הפוך). נסמן את הייצוג הבינארי כ $b_{k} \dots b_{2} b_{1} b_{0} : b_{j} \in {0, 1}$ וכעת $i$ יהיה $\sum_{j = 0}^{k} b_{j} 2^{j}$ .
הסיבה שאני מזכיר את זה פה כי בצורה הבינארית אפילו יותר קל לגשת לאינדקסים של הילדים בערימה עבור הקודקוד באינדקס $i$ הנ״ל למשל

right child: b_{k} \dots b_{2} b_{1} b_{0} 1

left child: b_{k} \dots b_{2} b_{1} b_{0} 0

ואם נרצה לעלות ברמה ולהגיע לאינדקס של קודקוד האבא של $i$ :

father node: b_{k} \dots b_{2} b_{1}

מורידים פשוט את הספרה האחרונה.

אם נרצה למחוק איבר אנחנו יודעים איפה נמצא האיבר האחרון שאפשר למחוק באופן תקין (בסוף המערך) ונוכל פשווט להחליף בין הערכים בזמן קבוע, לזוז ולבצע החלפות כמו שהגדרנו בזמן לוגריתמי.

נקודה חשובה, המחיר שאנחנו משלמים על הבנייה הזאת של ערימה, היא חיפוש, בניגוד לעץ חיפוש בינארי, כאן לא מוגדר באמת יחס סדר על האיברים ולכן נצטרך לחפש איבר בזמן ליניארי בתוך המערך, רק לאחר מציאת האינדקס שלו נוכל לבצע את שאר הפעולות . ההערה הזאת חשובה, כי בעצם אם המבנה שלנו נועד למחוק ולחפש איברים בתוכו אולי ערימה היא לא המצב המתאים, ערימה נועדה לממש באופן האידיאלי את התור עדיפויות שהגדנו, ומטרתו העיקרית היא הסרה של הראש וזמן לוגריתמי ומשיכתו בזמן קבוע.

בנייה של ערימה

לכאורה, נוכל לבנות את הערימה על ידי הכנסה של האיברים למערך ריק או עץ ריק וזה ייקח לנו בדומה למימוש של עץ בינארי $Ω (n \log n)$ . אבל בתחילת הפרק אמרנו שאנחנו יכולים לבנות ערימה בזמן ליניארי לכמות האיברים.
לשם הבנייה של הערימה ב $O (n)$ נגדיר פונקצייה הנקראת Heapify(i,j) . שעובדת על תת המערך שבאינדקסים הללו. באופן מדוייק יותר מה שהיא תעשה היא תעבוד על תת העץ של תת המערך הזה כאשר השורש הוא $v_{i}$ אבל תתעלם מכל הקודקודים שהם גדולים (או קטנים, תלוי בסוג הערימה). הכוונה היא, שכאשר אנחנו מתייחס לתת המערך $A [i \dots j]$ אנחנו לא באמת עובדים על כל תת המערך הזה אלא רק אל אלה שמתייחסים לתת העץ ששורשו הוא $v_{i}$ למשל עבור heapify(2,10) האיברים באפור הם אלה שנתמודד איתם.
Pasted image 20220628014204.png

בסופו של דבר, המטרה היא להפוך את הערכים של האינדקסים האפורים (אלה שהם חלק מתת העץ של תת המערך שנתנו בקלט) לערימה תקינה.

לשם הנוחות שבהגדרת הפעולה הזאת, נניח שכל תתי העצים של ששורשם הם הילדים של $v_{i}$ כלומר : $v_{2 i}$ ו $v_{2 i + 1}$ הם ערימות בעצמם :
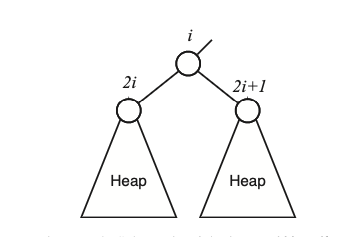
Pasted image 20220628014559.png
כעת הפעולה תעבוד באופן הבא

$check if: A [i] \geq A [2 i] and, A [i] \geq A [2 i + 1]$
אם תנאי זה מתקיים תת העץ שאנחנו עובדים עליו הוא כבר ערימה.
אחרת, נבצע החלפה של $A [i]$ עם הילד הגדול מבין השניים. נשמע טוב, אך כעת יש סיכוי ששברנו את תת העץ של אותו קודקוד שהחלפנו. במצב זה פשוט נבצע תיקון ריקורסיבי.

בפסודו קוד:
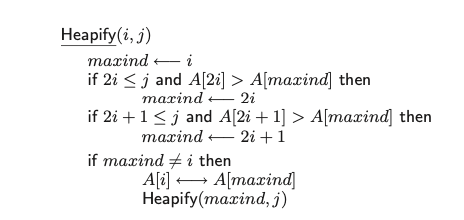
Pasted image 20220628015711.png
המשתנה maxing מחזיק בתוכו את האינדקס של השורש המקורי של תת העץ איתו אנחנו עובדים (גם אם הוא משתנה כתוצאה מהחלפה).

אנקדוטה החלפת משתנים:
אנחנו מכירים את השיטת הקלאסית להחלפת ערכים משתנים באמצעות משתנה עזר
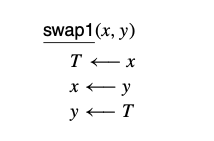
Pasted image 20220628015916.png
אך ניתן לעשות את זה בלי משתנה עזר על ידי האופרטור הבינארי $X O R$ באופן הבא
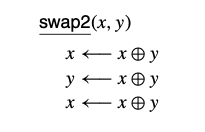
Pasted image 20220628015938.png

function swapWithXOR (a, b) {
    a = a^b;
    b = a^b;
    a=a^b;
    console.log("result => a: " + a + ", b: " + b)
}

(להסבר נוסף על אופרטורים בינאריים לחצו על הלינק).

הוכחה של הטענה:
בשורה השנייה אנחנו מבצעים את זה
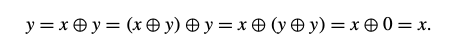
Pasted image 20220628020442.png

ובשורה השלילית
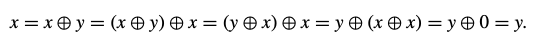
Pasted image 20220628020452.png

חישוב זמן הריצה של הבנייה

נבין רגע איך בונים את הערימה באופן כללי על ידי הפסודו קוד הבא
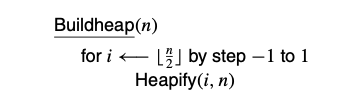
Pasted image 20220628020709.png

אנחנו בונים את הערימה מלמטה למעלה ויש לזה חשיבות רבה. אנחנו יודעים מ הוכחות בעצים שיש לעץ כמעט מלא $\frac{n}{2}$ (עם עיגול כלפי מעלה) עלים. וכל עלה הוא כמובן ערימה בפני עצמו. הבנייה מלמטה למעלה נבנת בצורה כזאת שמספר ההחלפות שנצטרך לעשות כל פעם חסום בגובה שטוח יותר מהגובה של כל הערימה במלואה. רק בקריאה האחרונה נגיע לעץ בעומק המלא.
באופן מתמטי, אם עומק העץ המלא הוא $k$ יש $2^{1 + k} - 1$ קודקודים (בגלל שהשלב הראשון בעץ מתחיל מ 0 צריך להוסיף 1 לשלב האחרון כדי לקבל את גובה העץ האמיתי) אבל כל איטרציה אנחנו עובדים עם עץ נמוך יותר ולכם נקבל

\sum_{i = 0}^{k - 1} 2^{i} (k - i) < n

אני לא אפרט למה זה נכון, בגדול מדובר פשוט בסכום של סדרה חשבונית ונקבל

2^{k + 1} - 2 - k = 2^{k + 1} - 1 - 1 - k = n - 1 - k < n

ולכן פעולה הבנייה שייכת ל $O (n)$ כמו שרצינו.

HeapSort

אנחנו עוד נדבר על סוגי מיונים חשובים בהמשך, אבל הייתי רוצה לדבר על המיון הזה בפרק המתאים לו כיוון שהקונספט עוד ברור לכל מי שקרא עד כה.
נניח שיש לנו מערך עם $n$ איברים. אנחנו יודעים שבבניית הערימה (בלי הגבלת הכלליות נניח שזה ערימת מקסימום) הערך הכי גבוה יהיה למעלה. נוכל לשלוף אותו ולשים אותו בסוף המערך, ולבצע שוב heapify על על תת המערך בלי האיבר האחרון. באופן זה נוכל למיין את הערימה בלי שום מקום נוסף.
Pasted image 20220628092923.png

סיבוכיות אחרי כל בניית הערימה והחלפת האיבר הראשון אנחנו יודעים בוודאות שכל תתי העצים לאחר החלפה בין השורש לבין האיבר האחרון הם ערימות בעצמם, ולכן התיקון יהיה חסום במספר האיטרציות שביצענו כלומר

\sum_{j = 1}^{n} \log j < \sum_{j = 1}^{n} \log n = O (n \log n)