#concurrency

SIMD

בסיכום זה נתמקד באחד מהכלים לבצע תכנות מקבילי העונה לשם SIMD - single instruction multiple data. בד״כ מדובר בחומרה ופקודות מעבד (משתנה לפי ISA) שמבצעות את אותה פקודה על מספר יחידות מידע בבת אחת.

הדיאגרמה הבאה מציגה את סוגי התכנות המקבילי הקיימים לפי Flynn's taxonomy

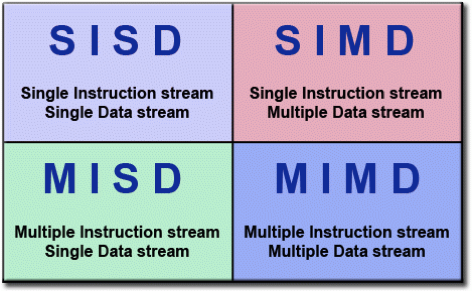
Pasted image 20240324220832.png

למשל, נוכל לקחת שני וקטורים A,B בגודל 4 ולבצע סכימה של $A [i] + B [i]$ לכל $i \in [0, 3]$ בבת אחת.

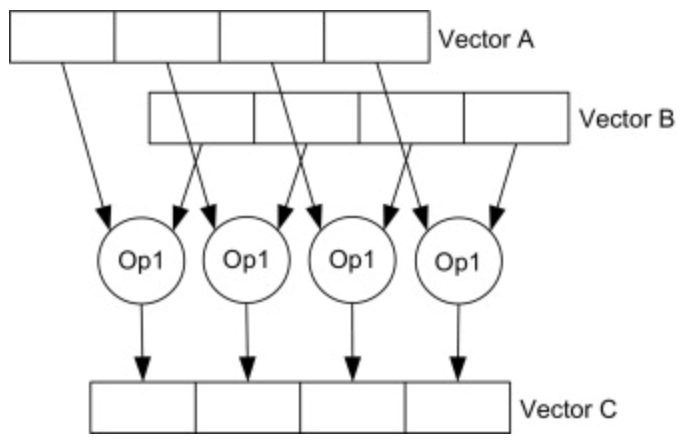
Pasted image 20240324221151.png|250

AVX

אחד הרכיבי חומרה העיקריים במערכות x86 לביצוע פקודות SIMD הם רכיבי הAVX Advanced Vector Extensions.

נזכיר שב x86-64 Assembly ישנם general purpose registers לחישובים אריתמטיים של integers בייצוג signed ו unsigned ולאריתמטיקת כתובות. החומרה הזאת לא תמכה בחישובים אריתמטיים של Floating Point ברמת החומרה.

לאחר מספר עשורים הוכנסו רכיבי ה AVX שתומכים גם באריתמטיקה של מספרים עשרוניים וגם באריתמטיקה וקטורית לוקטורים בגודל של עד 256 ביט.

Pasted image 20240324223350.png|200

הregisters הללו הם מעין תחליף לכל מה שקשור לקוד שמבצע מניפולציה על float ו double. כמו שיש registers שיש להם תפקיד ב רגיסטרים ה״רגילים״ שאנחנו מכירים (rax כערך החזרה למשל). כך גם לregisters הנ״ל יש תפקידים

xmm0-תופס את הארגומנט הראשון וגם את ערך ההחזרה
xmm1-xmm7 - העברת שאר הארגומנטים לפונקציה
xmm9-xmm31- שמירת ה Caller saved.

scalar and packed modes

כפי שציינו הרגיסטרים האלה תומכים גם באריתמטיקה סקלרית של floats וגם באריתמטיקה וקטורית. לכן ה ISA צריך לתמוך בפקודות שמאפשרות לחומרה להבין בשביל מה אנחנו רוצים להשתמש בחומרה הזאת.

מבנה ההוראות הכללי עבור הפקודות האלה נראה ככה

<OP> <s/p> <s/d>

$< O P >$ -הפקודה עצמה, יש המון פקודות כמו הזזה של ערכים, חיבור, חיסור וכו׳. כל הפקודות של AVX יתחילו ב 'v' (יש מערכת ישנה יותר שנקראת SSE ששם הפקודות הן בלי 'v').
$<s/p>$ - קובעים האם אנחנו רוצים לעבוד עם data מסוג scalar או עם packed
$<s/d>$ - single precision או double precision. לפי הבחירה הזאת אנחנו נקבע גם כמה ערכים יש לנו בוקטור (אם עובדים עם doubles אז ברגיסטר xmm יכולים להיות 2 מספרים double או 4 מספרי float).

דוגמה: $vaddpd xmm1, xmm2$ . פקודת AVX שמבקשת לחבר את xmm1 ו xmm2 בpacked mode ועם double precision.

בניגוד לפקודות מהרגיסטרים של integers, כאן התוצאה יכולה גם להכנס לרגיסטר שלישי שנרצה (נראה דוגמה בהמשך)

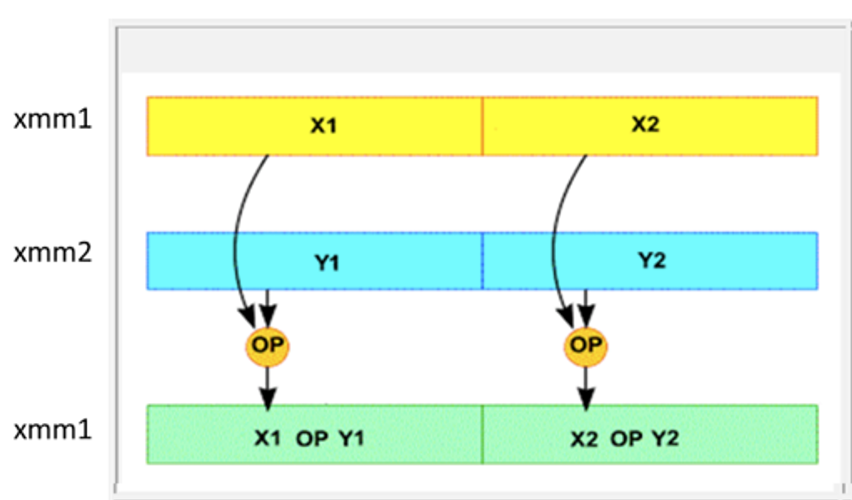
Pasted image 20240324225300.png|250

אם נחליף ל single precision נקבל:

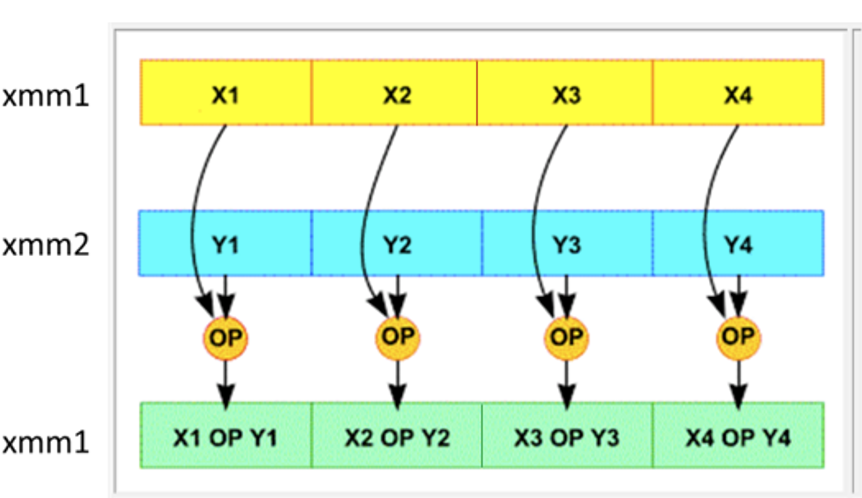
Pasted image 20240324225152.png|250

החישובים המצויינים בתמונה נעשים באופן מקבילי לחלוטין.

אם היינו משתמשים ב scalar mode היינו מבצעים את פעולת החיבור רק על 32/64 הביטים הראשונים.
האופציה של scalar קיימת מכיוון שהרגיסטרים האילו מיועדים לכל הסוגים של חישובים float-point ולא בהכרח חישובים וקטוריים.

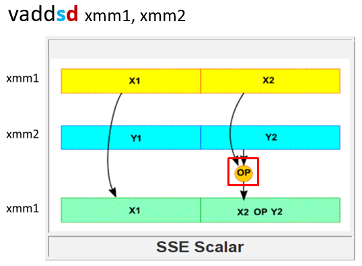
Pasted image 20240324225641.png|250

פקודות אריתמטיקה

הפקודות הנ״ל הם פקודות אריתמטיקה בין מספרים עשרוניים מסוג float או double (הפקודות ל packed data זהות, רק צריך לשנות את ה s ל p כפי שהסברנו)
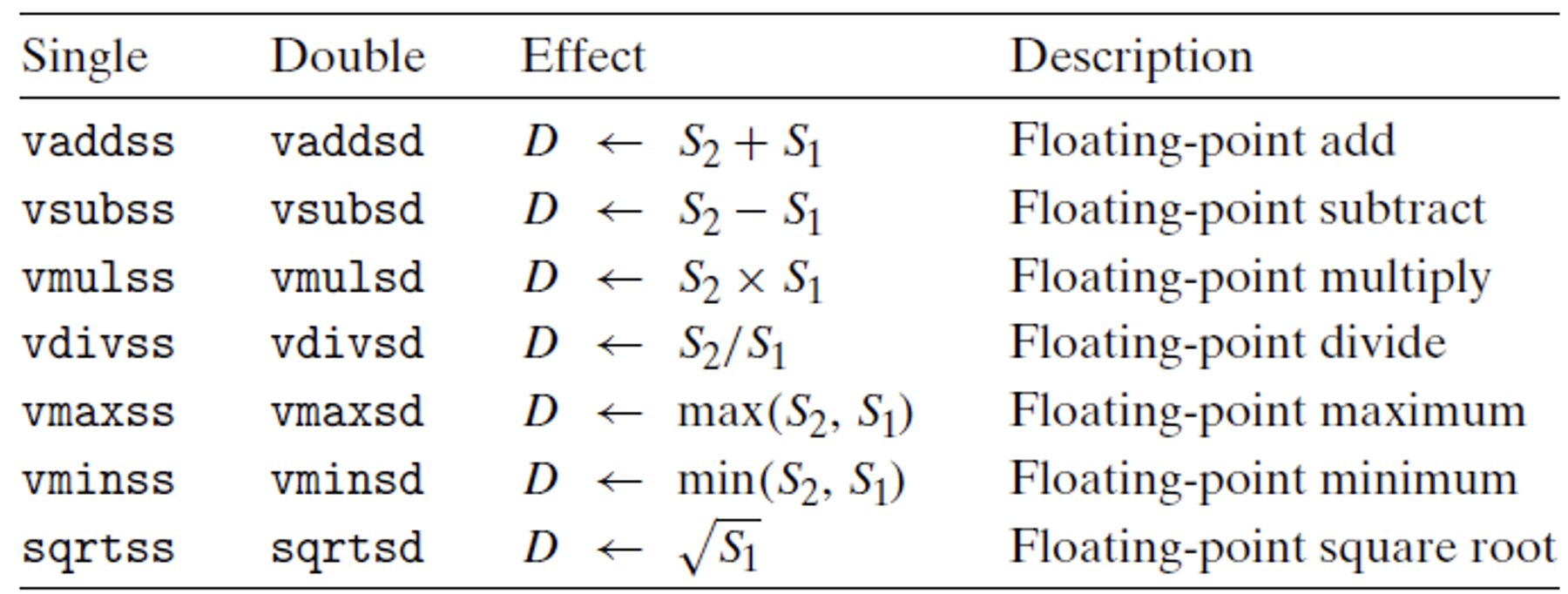
Pasted image 20240324230044.png|350

$S_{1}$ (הרגיסטר האמצעי מבין השלושה) - יכול להיות גם כתובת זכרון, נזכיר שהסינתקס לגשת לכתובת זכרון היא '(reg)'.
שאר הארגומנטים לא יכולים להיות כתובת אלא רגיסטרים של AVX בלבד.
אם נביא רגיסטר שלישי בארגומנטים אז התוצא תכנס אליו:
- הפקודה vmulsd %xmm0, %xmm1, %xmm4 תעשה - xmm4 ← xmm1 $\cdot$ xmm0
- הפקודה vmulps %ymm0, (%rcx), %ymm1 תעשה - $y m m 1 \leftarrow [b_{7} \cdot 𝑎_{7}, \dots, b_{1} \cdot a_{1}, b_{0} \cdot a_{0}]$ כאשר rcx מצביע ל128 הביטים שבהם נמצא הוקטור $[b]$ .
- אם לא ניתן ארגומנט שלישי התוצאה תכנס לארגומנט הראשון.
נשים לב שלפקודה sqrt אין גרסה עם 'v' כי זאת פקודה של AVX בלבד.

פקודות move

נזכיר שmove אלא פקודות שמאפשרות להזיז תוכן בין רגיסטרים או בין memory לרגיסטר או בין רגיסטר לmemory.

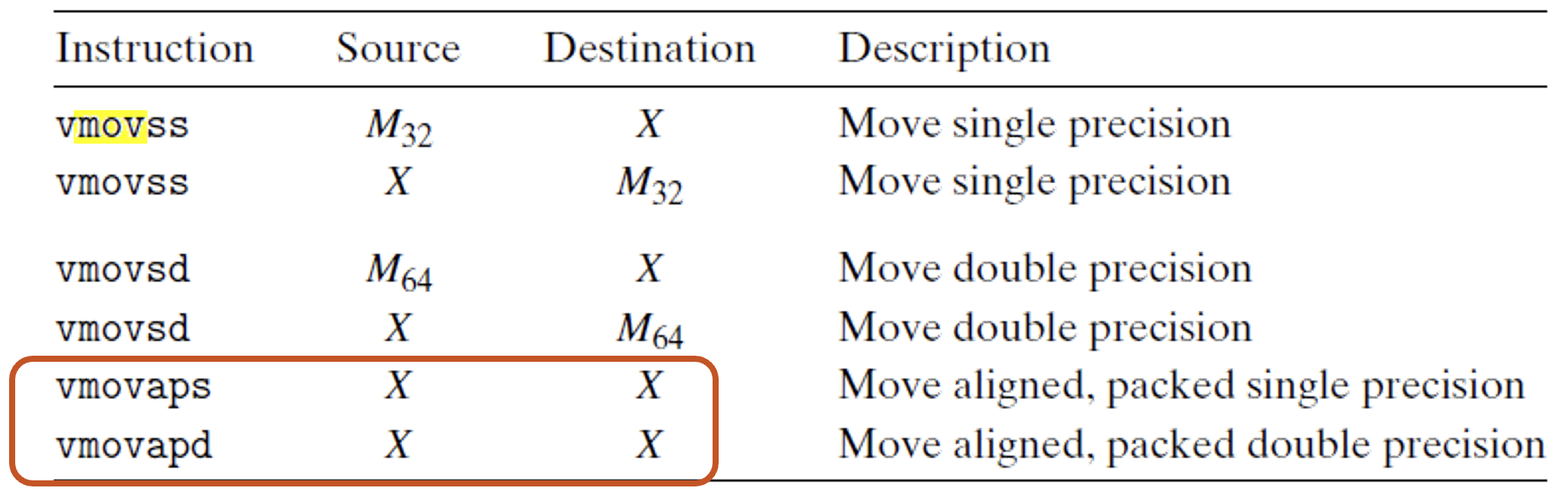
Pasted image 20240324231800.png

סינתקס של פקודה:
- v-vector instruction
- ss-scalar single
- sd-scalar double
- ps-packed single
- pd-packed double
- $M_{32}$ ו $M_{64}$ - לוקח 64 או 32 ביט מהכתובת הנתונה.
- X מייצג רגיסטר של AVX.
addressing mode זהה לפקודת mov הרגיל
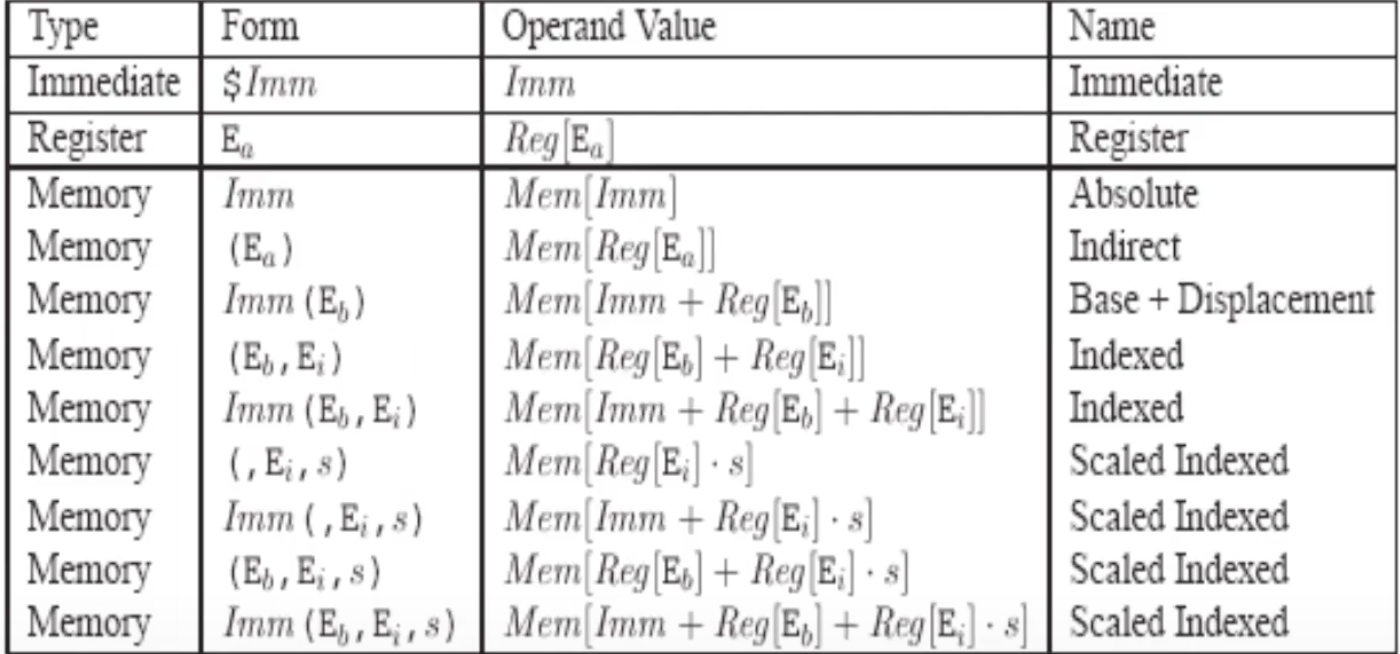
מידע בזכרון חייב להיות alignedלפי הגודל של הרגיסטר בביטים. הסיבה לכך היא ביצועים שקשורים לCache, השמירה ב cache היא ברמת הבלוקים שנקבע לפי כמות הביטים בכתובת שמיועדת לblock offset. לכן מידע שהוא לא aligned עלול לגרום לכך שdata struct אחד יתפוס שתי lines של cache. דבר שפוגע מאוד בביצועים.
- לכן האות a בפקודה מחייב שהdata שקוראים מהזכרון יהיה aligned של 16 בתים (128 ביטים), אחרת תזכר שגיאה.
- זה רלוונטי רק ל mov בין רגיסטר וזכרון כי בין שני רגיסטרים אין אפשרות שזה יקרה.

פקודות conversion

המרה לintegers:
Pasted image 20240324235921.png

v-vector instruction
cvtt - convert with truncation המרה עם חיתוך (עיגול כלפי מטה), המקרה הזה הפיכת החלק שמייצג את השבר במספר העשרוני ל 0.
ss2si - מספר float ל int
sd2si- מספר double ל int
ss2siq, sd2siq - מספר double ל quad word integer.
ה source יכול להיות register X כלומר מסוג AVX או כתובת זכרון שמפנה ל float או double
היעד הוא תמיד register של 32 או 64 ביט רגיל.

Pasted image 20240325000839.png|300

הקוד מזיז מהכתובת שבה val נמצא את התוכל שלו ל xmm0.
מתבצע המרה מ xmm1 למספר quad word שאותו שמים ב rdi.

המרה מinteger לfloat/double
Pasted image 20240325001046.png

v - vector
cvt - convert
si2ss/sd - המרה ל single או double
q - מסמל שגודל ה int הוא quad word.
נתעלם מ source 2 לרוב, פשוט נשים גם ב source 2 וגם ב destination את אותו רגיסטר.

המרה מ float ל double
אפשר גם להמיר מספרים עשרוניים ולשנות את רמת הדיוק שלהם באופן הבא

Pasted image 20240325002944.png

vcvtpd2ps - לוקחת double וממירה לfloat
vcvtss2sd - לוקת float וממירה לdouble.

הסיבה שבאפור נראה כאילו עברנו ממערך בגודל 4 למערך בגודל 2 כאשר המרנו ל double והפוך כאשר המרנו ל float היא שבפועל זה באמת מה שקורה, בגלל שמדובר גם בוקטורים אמרנו שיכול להיות לי בdouble שתי מספרים וב float ארבעה, אבל אם אני ממיר אני או מרפס באפסים או מוותר על שתי המספרים בבתים הגבוהים

כמובן שהפעולה הזאת עלולה לגרום לנו או לאבד דיוק של המספר או להרחיב את הדיוק שלו במחיר של עוד 4 בתים.

דוגמה
נסתכל על קטע הקוד הבא

double func(double w, int x, float y, long z) {
	return y*x - w/z;
}

נשים לב לכמה דגשים:

x ו z נשמרים ב rdi ו rsi בהתאמה.
w ו y נשמרים ב xmm0 ו xmm1 בהתאמה.
$y \cdot x$ זה חישוב שמערב int ו float ולכן צריך להמיר את x ל float.
תחת אותו הסבר צריך להמיר את z ל double.
פעולת החיסור היא בין float ל double ולכן צריך להמיר את ה float ל double

func: 
	vcvtsi2ss edi, xmm2, xmm2 
	vmulss xmm1, xmm2, xmm1
	vcvtss2sd xmm1,xmm2
	vcvtsi2sdq rsi xmm1, xmm1
	vdivsd xmm1, xmm0, xmm0
	vsubsd xmm0 xmm2 xmm0
	ret

השורה הראשונה ממירה את x לfloat ושמה אותו ב xmm2
השורה השנייה מכפילה בין y ל x ושמה את התוצאה ב xmm1
השורה השלישית ממירה ל double את התוצאה ושמה ב xmm1.
השורה הרביעית ממירה את z ל double
השורה החמישית והשישית מבצעות את החילוק והכפל.

דוגמה 2:

.section .data .align 16
	val: .float 42.42

.text 
.globl main

main:
	vmovss val(%rip), %xmm0 # xmm0 <- [0,0,0,42.42]
	vcvttss2si %xmm0, %eax # eax <- 42
	ret

vmovss - מכניסים לתוך הוקטור xmm0 את התוכן שמה שנמצא בכתובת של val ב relative address mode כלומר הכתובת של val היא רלטיבית לערך של rip. זה מאפשר לקוד להיות position independent, כלומר, אין צורך לחשוש שהכתובת שval תקבל לא תהיה קיימת בין ריצות של תוכניות
vcvttss2si- פקודה שממירה float ל int ושמה אותו ב eax.

constants

ב AVX לא ניתן לרשום immediate כמו בregisters הרגילים בפעולות אריתמטיות. לכן יש צורך לטעון אותם ישירות מהזכרון.
השמירה בזכרון תעשה או על ידי שמירת הייצוג הבינארי $. b y t e$ או על ידי שמירת המספר השלם כפי שאותם ביטים היו מייצגים אותו ב IEEE.

למשל עבור הפונקציה

double f(double temp) {
	return 1.8 * temp + 32.0;
}

הקוד יראה ככה
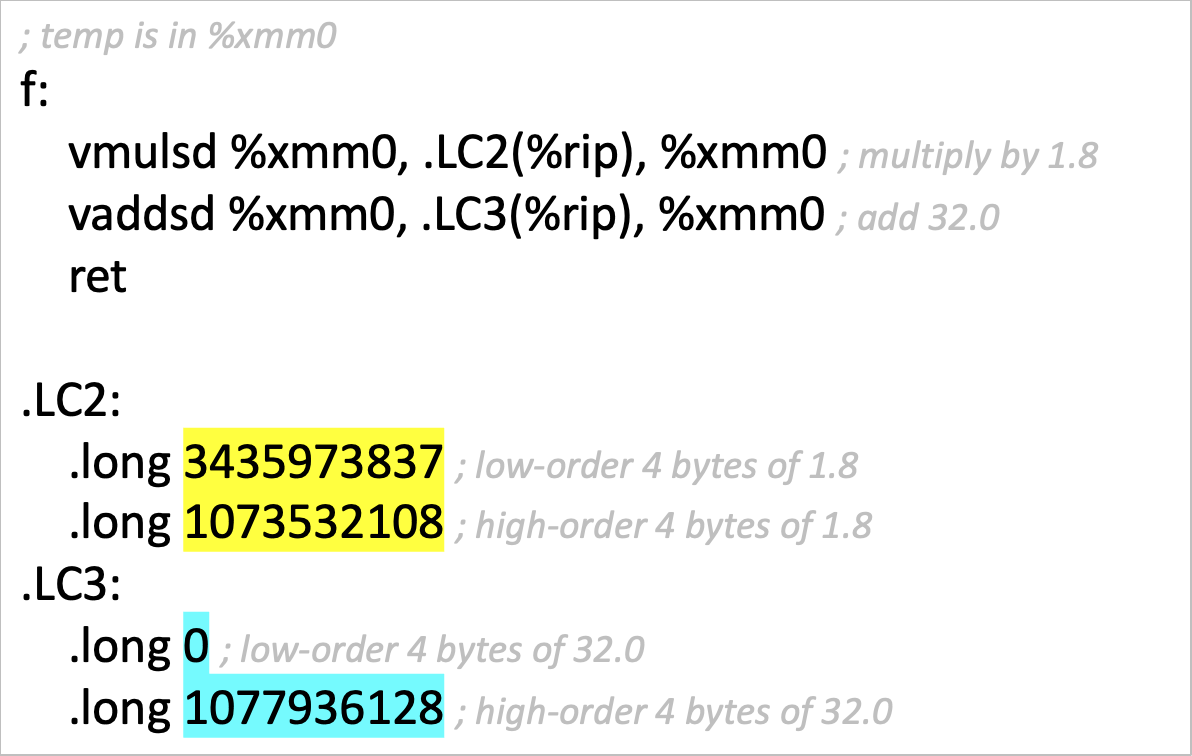
Pasted image 20240325011330.png|350
הסיבה שכאן שמרנו ה4 בתים בנפרד היא בגלל endianness. היה אפשר גם לשמור את כל ה8 בתים בבת אחת אבל היה צריך לשים שהייצוג צריך להיות לפי האינדיאניות של המערכת.

bitwise

Pasted image 20240325102933.png|350
צריך לשים לב שהפקודות הנ״ל עובדות על packed data ולכן הן מעדכנות את כל הבתים ב xmm registers גם אם השתמשנו רק בחלק מהם.

Pasted image 20240325104535.png|300
קטע הקוד הבא הופך מספרים בוקטור לתצורה השלילית שלהם באמצעות xor. המספרים שרשומים שם פשוט מרכיבים מספר בינארי שה MSB שלו הוא 1 וכל השאר אפסים. לכן הוא יהפוך את הביט סימן עבור כל float בוקטור וכל השאר יחזיר את אותו הערך של הביט שהיה מקודם בעת ביצוע xor.

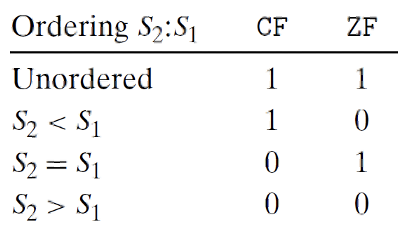
Comparison

Pasted image 20240325104901.png|300

S2 חייב להיות xmm.
S1 יכול להיות גם כתובת זכרון.
הפעולה הזאת מדליקה את ה EFlags registers המוכרים ומדליקה גם כמה flags פחות מוכרים
- unordered אם אחד המספרים הוא NAN
- parity אם התוצאה היא NAN

Pasted image 20240325105229.png|200

נראה קוד c שבודק האם מספר הוא NAN ואיך זה נעשה באסמבלי

f(float x) {
	if(x<0) return -1;
	if(x==0) return 0;
	if(x>0) return 1;
	if(isnan(x)) return 2;
}

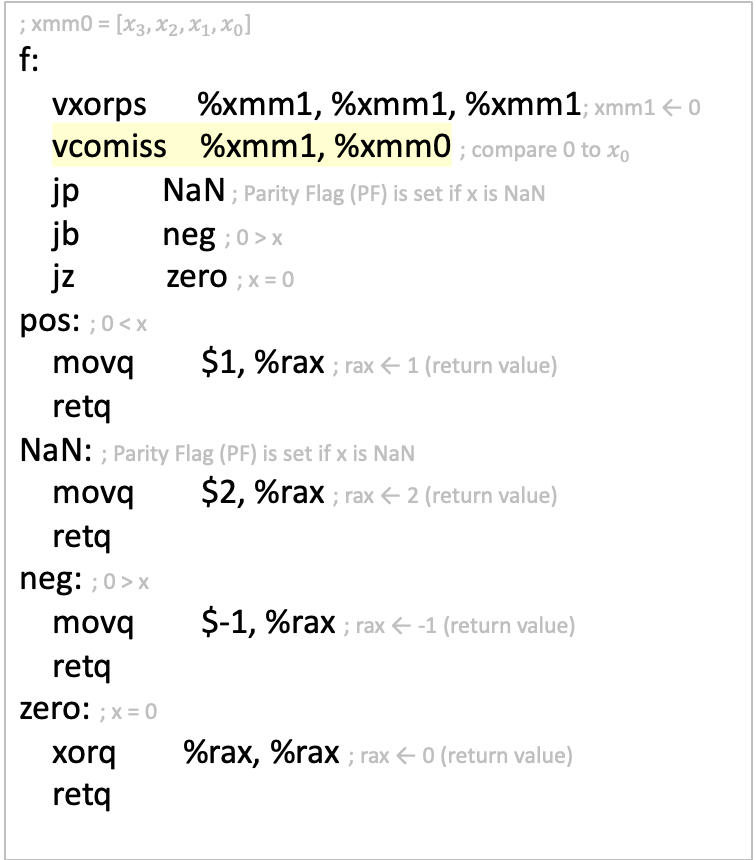
Pasted image 20240325111650.png|350

הקוד בודק אם jp דולק (parity flag) ואם כן הוא קופץ לקוד NaN ומחזירים 2.

Printf על float numbers
נסתכל בקוד האסמבלי הבא

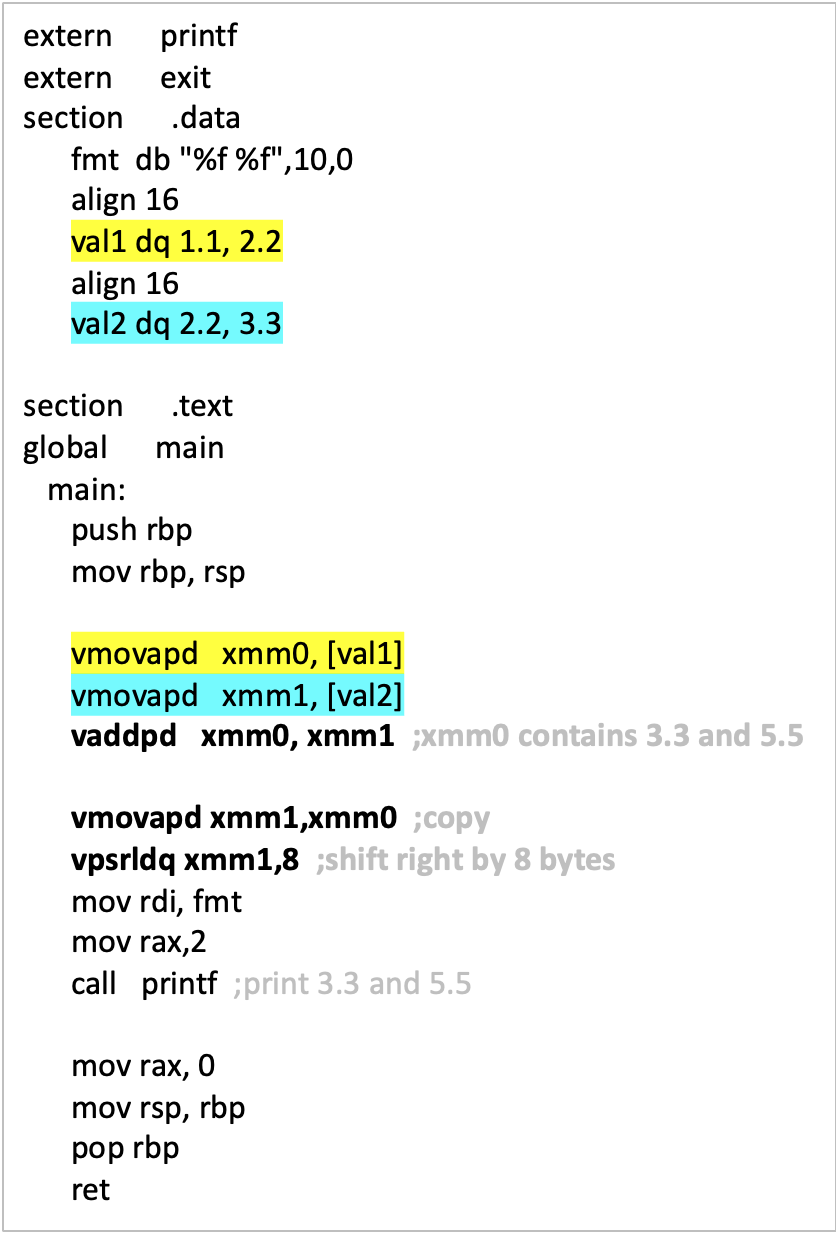
Pasted image 20240327000906.png|300

הקוד מעתיק מהזכרון את הערכים ל xmm0 ו xmm1 בתצורת packed double.
מחברים בצורה מקבילית בין שני הוקטורים.
מעתיקים את התוצאה שנמצאת ב xmm0 ל xmm1
מזיזים את xmm1, שמונה בתים ימינה- את זה עושים כדי לחלץ את הערך השני בוקטור.
1. fmt הוא הפורמט שprintf מקבל והוא מדפיס שני floats, במצב זה printf מחפש אותם ב low ordered bytes של xmm0 ו xmm1 כי printf מתייחס לוקטורים האלה כסקלר.
מעבירים את המידע שצריך כמו מספר הארגומנטים והפורמט ל printf ומפעילים אותו.
נשים לב שהשתמשנו ב align כדי למנוע התנהגות לא צפויה כפי שציינו כבר שיכול לקרות.

חישובים אריתמטיים

נחשב את הנוסחה של שונות משותפת .

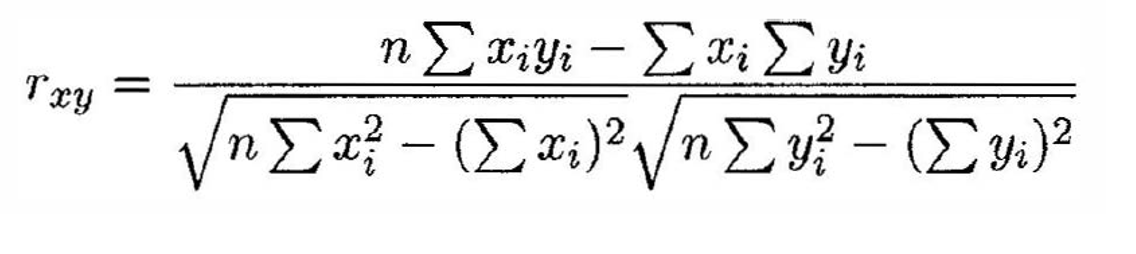
Pasted image 20240327001401.png|300

בקוד c סדרתי הפתרון די פשוט

#include <math.h>
double corr ( double x[ ], double y[ ], long n ) { 
   double sum_x, sum_y, sum_xx, sum_yy, sum_xy; 
   sum_x = sum_y = sum_xx = sum_yy = sum_xy = 0.0; 

   for (long i = 0; i < n; i++ ) { 
        sum_x += x[i]; 
        sum_y += y[i]; 
        sum_xx += x[i]*x[i]; 
        sum_yy += y[i]*y[i];      
        sum_xy += x[i]*y[i]; 
   } 

   return (n*sum_xy-sum_x*sum_y) / 
                sqrt((n*sum_xx-sum_x*sum_x) * 
                (n*sum_yy-sum_y*sum_y)); 
}

נשים לב לרמז שמאפשר לנו להבין שניתן להשתמש ברכיבי AVX לייעול האלגוריתם -
יש כאן מספר סכומים שמצטברים בכל איטרציה בנפרד ולבסוף מתחברים ביחס באיזשהו אופן.

הרעיון:

xmm0 יכיל בכל פעם זוג מהסכום של $x$
xmm1 יכיל בכל פעם זוג מהסכום של y
xmm2 יכיל בכל פעם זוג מהסכום של $x^{2}$
xmm3 יכיל בכל פעם זוג מהסכום של $y^{2}$
xmm4 יכיל בכל פעם זוג מהסכום של xy
נוכל לעצור כאן ולבנות לולאה שכל פעם זזה בקפיצות של 8 בתים או לעשות loop unroll ולהשתמש בעוד רגיסטרים כדי לצבור את האיברים הבאים ולזוז בקפיצות של 16 בתים ואף יותר.
בסופו של דבר, כל איבר בוקטורים שנשתמש בהם יכיל את הסכימה של האיברים הזוגיים במיקום הראשון ובמיקום השני את הסכימה של האיברים האי זוגיים (אם נבצע loop unroll אז הקפיצות בכל איבר בוקטור יהיו גדולות יותר מזוגיים ואי זוגיים).
מבצעים את הloop unroll באופן כזה שתהיה חוקיות בין הרגיסטרים, למשל xmm0 ו xmm8 יכילו את הסכומים של x וגם xmm1 ו xmm9 יכילו את הסכומים של y וכן הלאה (בקפיצות של 8).

Pasted image 20240327010629.png|300
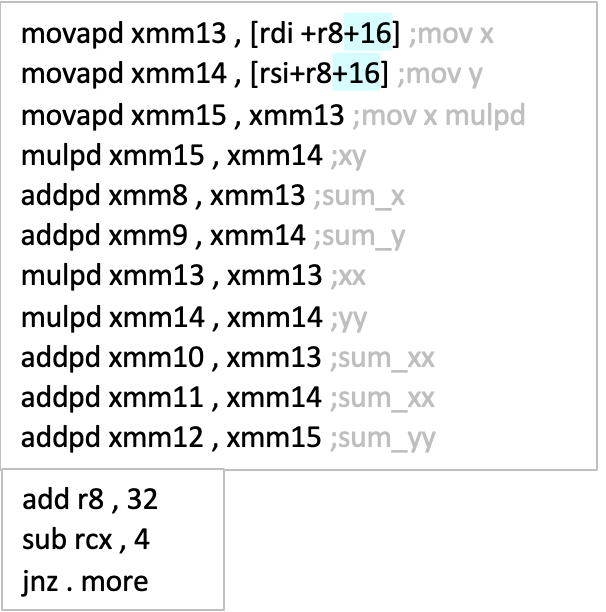
Pasted image 20240327010710.png|300

בסוף האיטרציות נקבל בערך משהו כזה

Pasted image 20240327010755.png|300

וכעת נוכל לסכום את כולם ביחד

Pasted image 20240327011252.png|300

horizontal add
כעת לחלק האחרון שנשאר, לחבר את האיבר הראשון בכל וקטור עם האיבר השני שלו, לשים את התוצאה ב8 הבתים הראשונים ולקבל מספר double שהוא התוצאה בכל הרצויה לכל חלק (מעין מעבר בין packed ל scalar).

את זה נעשה עם הפקודה haddpd. הקלט שלה הוא שני רגיסטרים/ רגיסטר ווקטור והיא מבצעת בידיוק את הנ״ל עבורם ושמה את התוצאה בכל איבר בוקטור הקלט הראשון.

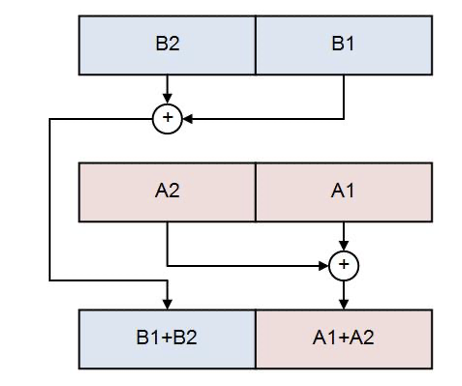
Pasted image 20240327011700.png|250
Pasted image 20240327011640.png|250

כעת כל שנשאר לעשות הוא

להמיר את n לdouble באמצעות cvtsi2sd (convert scalar int to scalar double).
לבצע את פעולות הכפל והחילוק על התוצאות שהתקבלו כתוצאה מhadd ולהחזיר את התוצאה ב xmm0

Pasted image 20240327110808.png|300
Pasted image 20240327110831.png|300

הקוד הנ״ל משתמש ברגיסטרים הבסיסיים ביותר בגודל 128 ביט. יכלנו להשתמש ברגיסטרים של AVX (ymm) כדי לשפר את התוצאה אף יותר

להחליף את הרגיסטרים xmmi ב ymmi.
להוסיף v לפני כל פקודות האריתמטיקה
להשתמש ב vhaddpd - כעת יש 4 ערכים בוקטור אז הפקודה סוכמת את השניים הראשונים ושמה אותם במקום הראשון של הוקטור ואת השניים האחרונים ושמה אותם במקום האחרון של הוקטור.
להשתמש ב vextractf128 כדי שתי ערכים עליונים מוקטור ymm לרגיסטר xmm .

vshufps

הרבה פעמים נרצה לבצע פעולה מתמטית של וקטור עם פרמוטציה על עצמו. לשם כך משתמשים בפקודה vshufps שמקבלת וקטור של ארבעה floats כקלט, רגיסטר יעד, ומספר בקרה (מספר שקובע את ההתנהגות של הפקודה ברמה מסויימת, במקרה הזה את סדר האיברים).

לדוגמה, הפקודה

vshufps xmm1, xmm0, xmm0, 0b 01001110

תיקח את הוקטור xmm0 ותמקם את האיברים בxmm1 לפי המספר הבינארי 01001110, כל שני ביטים מייצגים את האינדקס בוקטור xmm1 מבחינת המיקום שלהם (שני הביטים הראשון מייצגים את המיקום ה 0 בxmm1) וגם מבחינת הערך שלהם (למשל 01 מייצג את האינדקס 1 בxmm0). כך בעצם מתבצע הshuffle , באינדקס i בxmm1 נמקם את המספר לפי האינדקס שנקבע לפי מספר הבקרה.

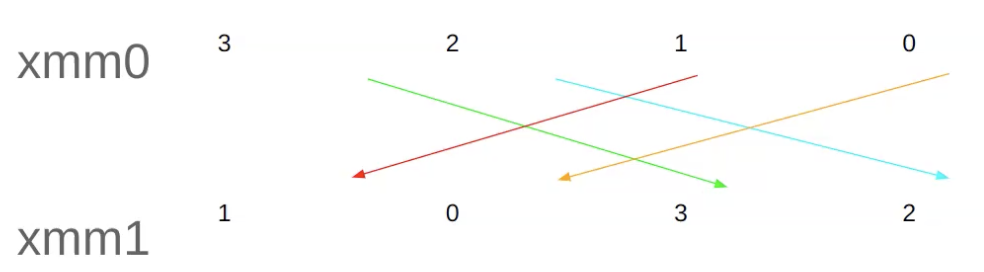
Pasted image 20240330185633.png|300

נשים לב ששמנו את xmm0 כמקור נוסף, בקונבנצייה שמים בשניהם את אותו הרגיסטר.

נראה דוגמה שמשתמשת בפקודה הזאת, נבנה תוכנית שנקראת xysum, מקבלת שני וקטורים x,y של floats באורך n ומחשבת את

s u m (x y) - s q r t (s u m (x^{2}) + s u m (y^{2}))

.intel_syntax noprefix

.section .text
.globl calc
# float calc (float x[], float[] y, long n) 
# calculating sum(xy) - sqrt(sum(x^2) + sum(y^2))


calc:
    # x - rdi
    # y - rsi
    # n - rdx, assuming n divides 4 for simplicity

    # calculating xy in xmm2
    # calculating x^2 in xmm3
    # calculating y^2 in xmm4
    vxorps xmm2, xmm2, xmm2
    vxorps xmm3, xmm3, xmm3
    vxorps xmm4, xmm4, xmm4

    # the loop
    xor r8, r8 # defining byte counter in r8
    xor r9, r9 # defining loop counter in r9
.for_loop:
    cmp r9, rdx # r9 - rdx
    jge .end_for_loop # if r9 - rdx >= 0 then jump

# inside the loop
    vmovaps xmm0, [rdi + r8] # loading x value
    vmovaps xmm1, [rsi + r8] # loading y value

    # calculating xy
    vmulps xmm5, xmm0, xmm1
    # adding xy to sum(xy)
    vaddps xmm2, xmm5, xmm2

    # calculating x^2, and adding it to sum(x^2)
    vmulps xmm0, xmm0, xmm0
    vaddps xmm3, xmm0, xmm3
    
    # calculating y^2, and adding it to sum(y^2)
    vmulps xmm1, xmm1, xmm1
    vaddps xmm4, xmm1, xmm4

    add r8, 16 # increasing byte counter
    add r9, 4 # increasing loop counter

    jmp .for_loop # jumping to the start of the loop

.end_for_loop:
    vaddps xmm3, xmm4, xmm3 # calculating sum(x^2) + sum(y^2)

    # summing the 4 seperate values in xmm2, to one value
    vshufps xmm6, xmm2, xmm2, 0b01001110
    vaddps xmm2, xmm6, xmm2
    vshufps xmm6, xmm2, xmm2, 0b10110001
    vaddps xmm2, xmm6, xmm2

    # summing the 4 seperate values in xmm3, to one value
    vshufps xmm6, xmm3, xmm3, 0b01001110
    vaddps xmm3, xmm6, xmm3
    vshufps xmm6, xmm3, xmm3, 0b10110001
    vaddps xmm3, xmm6, xmm3

    vsqrtss xmm3, xmm3, xmm3 #calculating sqrt(sum(x^2) + sum(y^2))


    vsubss xmm0, xmm2, xmm3 # calculating the final value
    ret

ניתן לראות שמכניסים לתוך הוקטורים בקפיצות של 16 ביטים כלומר 4 floats כל פעם.
בגלל שכל xmm שצובר את התוצאה מכיל בכל איבר בוקטור תתי סכומים בקפיצות של 4. נרצה להשתמש בshuf כדי לסכום את הוקטור עם תמורה על עצמו.
בסוף ריצת 2 הshuffle שרשומים בקוד בxmm הצובר יהיה בכל איבר בוקטור float שהוא הסכימה של כל האיברים.

AVX Text String Processing

רגיסטרים וקטוריים עושים עבודה מאוד טובה כאשר רוצים לעשות מניפולציה על מחרוזות.

נניח והיינו רוצים שבהינתן מחרוזת כלשהי, לקבל mask שקובע את המיקומים שבהם יש uppercase char במחרוזת.
למשל עבור המחרוזת Ab1cDE23f4gHi5J6 הmask יהיה 1000110000010010.

כדי להשיג תוצאה כזאת נשתמש בפקודות AVX הבאות
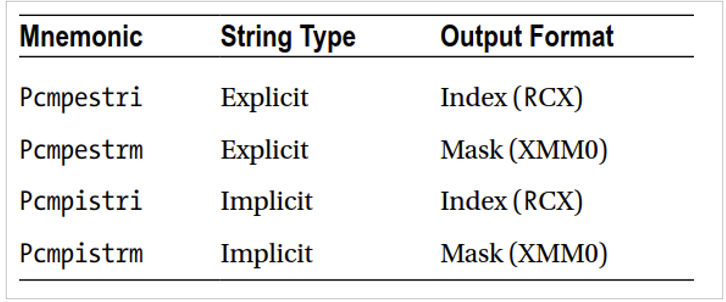
Pasted image 20240330154106.png|250

pcmp = packed compare
e - עבור מחרוזות עם explicit length (מעבירים גם את האורך כקלט). במידה ועובדים עם מחרוזות עם אורך מפורש הקלט עבור כל אחד מהסטרינגים צריך להיות בRAX וב RDX בהתאמה.
i - עבור מחרוזות עם implicit length (מניחים שבמחרוזת יש 0\ או שהיא תופסת את כל הregister).
stri - ערך החזרה הוא בצורת index ברגיסטר RCX.
strm - ערך החזרה הוא בצורת mask ברגיסטר XMM0.

ננסה לפתור את הבעיה המתוארת למעלה עם הכלים הללו:

הפקודה כמובן תהיה pcmpistrm כי הקלט הוא רק מחרוזת ונרצה את הפלט בצורת mask.
הפקודה מקבל שני רגיסטרים, XMM1 ו XMM2 ו מספר בקרה.
1. XMM1 - מכיל זוגות של טווחים (כל שני בתים מייצג טווח)
2. XMM2 - מכיל את המחרוזת עצמה.
3. ה control number קובע איזה פעולות נרצה לעשות על המחרוזת.
התוצאה תהיה ב xmm0 בצורת שתי בתים שאם מסתכלים עליהם כמספר אחד אז הייצוג הבינארי שלהם יהיה המאסק שקובע האם מספר נמצא באחד הrange שהגדרנו מראש. התוצאה נראת ככה ב xmm0 בגלל המספר בקרה. מספר בקרה אחר יניב פעולות אחרות ושמירתן בmask בצורה אחרת. הסיבה שזה בתצורת 2 בתים היא ש 2 בתים זה 16 ביטים שכל ביט i שקול לתו (בית) הi במחרוזת. 16 בתים זה המספר המקסימלי של תווים שוקטור יכול לקבל בבת אחת.

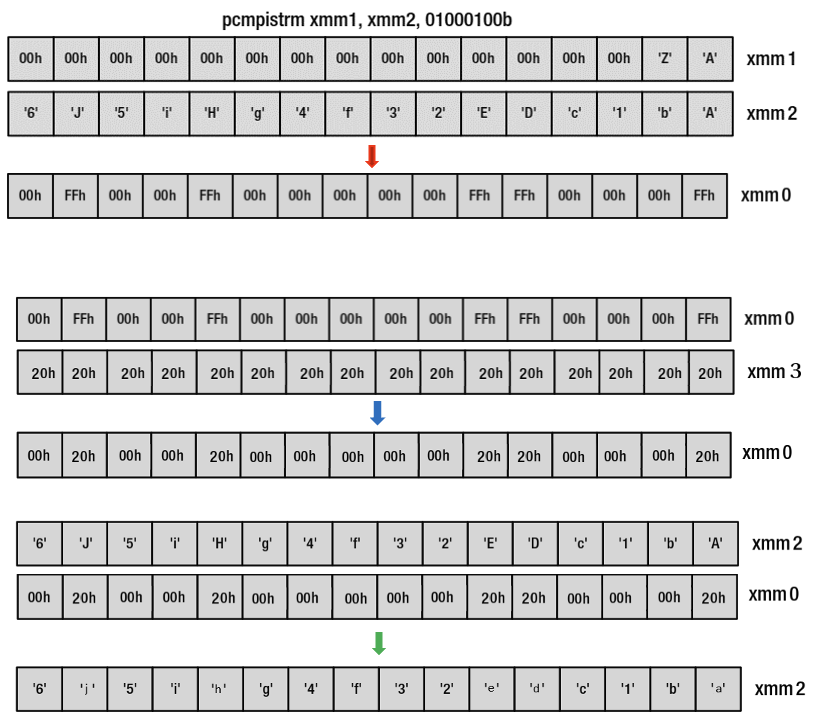
נסתכל מה קורה עבור הפקודה הבאה

pcmpistrm xmm1, xmm2, 00000100b

כאשר הרגיסטרים מכילים את התוכן הבא
Pasted image 20240330160624.png

XMM1 מכיל את הrange שהוא הטווח 'A'-'Z' .
XMM2 מכיל את המחרוזת בסדר הפוך.

הפעלת הפקודה תתן את הפלט הבא
Screenshot 2024-03-30 at 16.07.39.png

אם נסתכל על המספרים 48 ו 31 בייצוג בינארי נקבל

0x4831=0100100000110001b

נשים לב שהביט הראשון דולק עבור התו האחרון במחרוזת:

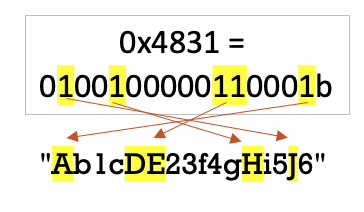
Screenshot 2024-03-30 at 16.08.58.png|200

היתרון הגדול כאן הוא שכל הפעולה הזאת קוראת בצורה מקבילית בגלל השימוש בAVX.

כעת נכתוב קוד אסמבלי שלוקח מחרוזת וממיר את כל האותיות שלה לאותיות קטנות


section .data
str: db ‘Ab1cDE23f4gHi5J6’
AZ_mask: db ‘A', ‘Z’	
                   times 14 db 0
imm: equ 01000100b
AZ2az_mask: times 16 db ('a' - 'A’)
result: times 16 db 0
            db `\n\0`	

extern printf
section .text
global main
main:
    enter
    movdqu xmm1, [AZ_mask]
    movdqu xmm2, [str]
    pcmpistrm xmm1, xmm2, imm
    movdqu xmm3, [AZ2az_mask]
    pand xmm0, xmm3
    paddb xmm2, xmm0
    movdqu [result], xmm2
    mov rdi, result
    mov rax, 0
    call printf
    leave
    ret

ב data section מגדירים את המחרוזת, את שני הmasks ואת הcontrol number.
1. times זה קיצור ללרשום x פעמים איזה תו או מחרוזת. times 16 db 0 למשל, שקול ללרשום 16 פעמים 0.
2. db=define bytes.
3. imm: equ=immediate equal to זה הגדרת קבוע בזמן קומפילציה.
שומרים ב xmm1 את AZ_mask ואת המחרוזת ב xmm2.
מריצים את הפקודה pcmpistrm xmm1, xmm2, imm.
1. התוצאה נשמרת ב xmm0.
2. נשים לב שה imm שונה ממה שהיה בדוגמה כעת הדגלנו את הביט השישי מה שמרחיב את התוצאה ל bytes במקום לביטים כמו בגרסה הקודמת. כלומר אם התו הi נמצא בטווח אז הביט הi ב mask יהיה 'FF'.
לאחר מכן טוענים את AZ2az_mask ל xmm3.
1. נשים לב שהmask הזה הוא 16 בתים שבכל בית יש ('a'-'A') שזה ההפרש בין הערכים הASCII שלהם כלומר 20h.
כעת עושים and בין xmm0 שמכיל את הmask הראשון לבין xmm3 שמכיל 20 בכל בית.
1. 20h בבינארית זה 00100000b. אם נעשה and עם FF נקבל שוב 20h.
2. הפעולה משאירה בבתים ש״דלוקים״ כלומר הבתים שבהם יש תווים באותיות גדולות את הערך 20h ובשאר יש 0.
paddb - עושה חיבור וקטורי ל packed bytes , כאשר עושים את זה בין xmm0 ל xmm2 התוצאה תהיה הערך הascii של התו בתוספת 20 אם הוא תו מסוג upper case או כלום עבור כל תו אחר.
1. תוספת של 20 לתו upper ממירה אותו ל lower (ההפרש בינהם הוא 20, זה למה שמנו 20 מלכתחילה).
מזיזים את התוצאה לכתובת שבה נמצא result ומעבירים אותו כקלט ל printf.

Pasted image 20240330170522.png|450

דגשים:

כפי שראינו כל ביט במספר בקרה משפיע על איך שנראה הפלט.
ניתן לתת multirange ברגיסטר הטווחים ותווים שנמצאים בלפחות אחד מבין הטווחים הללו יסומנו.
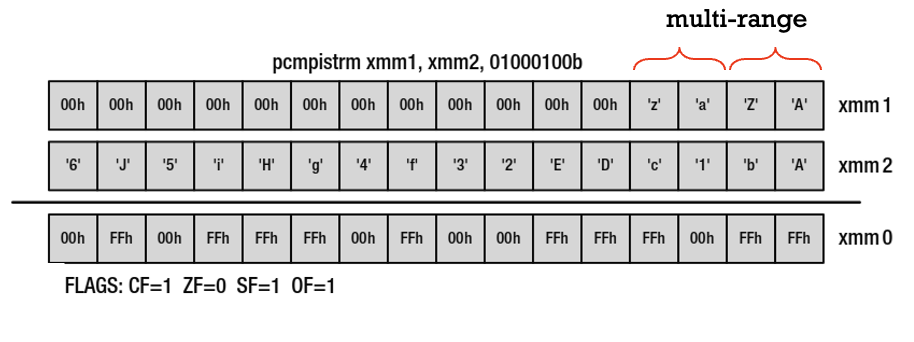
בכל סיום ריצה של הפקודה ה CF יהיה דלוק.
אם יהיה 0\ באמצע הריצה כלומר המחרוזת קטנה מ16 בתים, אוטומטית הפקודה תפסיק את פעולה ההשוואה ויסומן 0 בכל בית/ביט i שגדולים מאורך המחרוזת. כמו כן ה ZF יהיה דלוק.

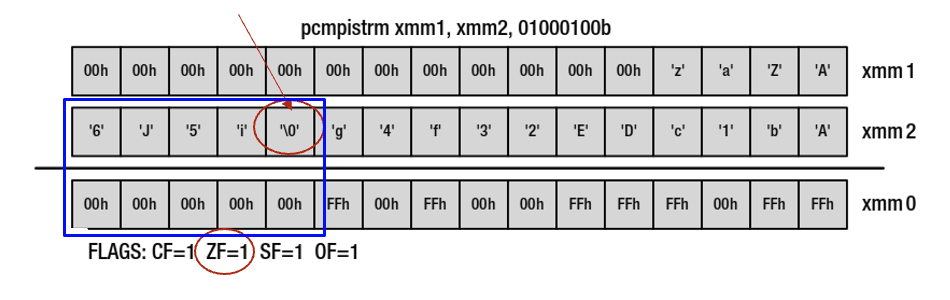
Pasted image 20240330170851.png|450

control number

הסיבה שעבדנו עם טווחים עד עכשיו היא בגלל ה control number והביטים שבחרנו שיהיו דלוקים בו. כאשר עובדים עם הcontrol number במקרה של pcmps מסתכלים על צמדים של ביטים- הצמד $(1 : 0)$ מסמל את הביט ה 0 והביט ה 1 וכן הלאה. במקרה של הדוגמאות הנ״ל אנחנו הדלקנו את הביט ה2 ולא את הביט 3 מה שקבע שההשוואה שנשתמש בה תהיה מסוג equal range.

ביטים נוספים יובילו להשוואות מצורה אחרת למשל:

אם שני הביטים יהיו כבויים כלומר 00. ההשוואה תהיה מסוג equal any כלומר בודקת האם התו ב XMM2 נמצא איפה שהוא ב XMM1.
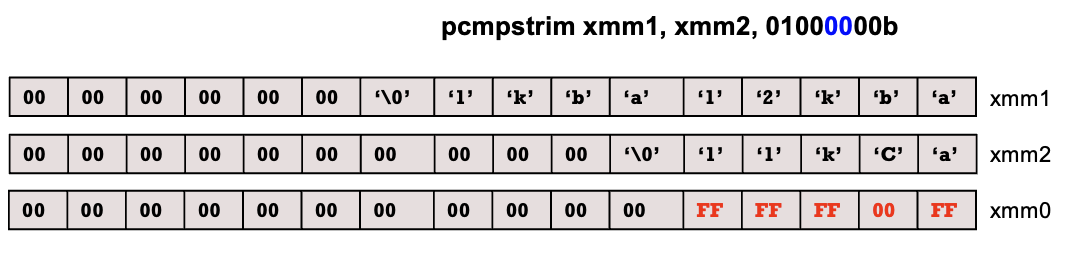
אם הביט ה3 היה דולק אבל הביט השני לא כלומר 10 ההשוואה הינה מדויקת- equal each כלומר האם הבית הi ב xmm2 שווה לבית הi ב xmm1
אם שני הביטים דולקים אז השוואה הינה equal ordered כלומר האם xmm1 הוא substring של השני ומסמנים ב mask את כל הבתים שבהם מתחיל הsubstring

מה המשמעות של כל צמד ביטים בcontrol number

הביטים 0,1 קובעים כיצד להתייחס למידע בתוך הוקטור (הפורמט)
הביטים 2 ו 3 עושים את מה שתיארנו למעלה

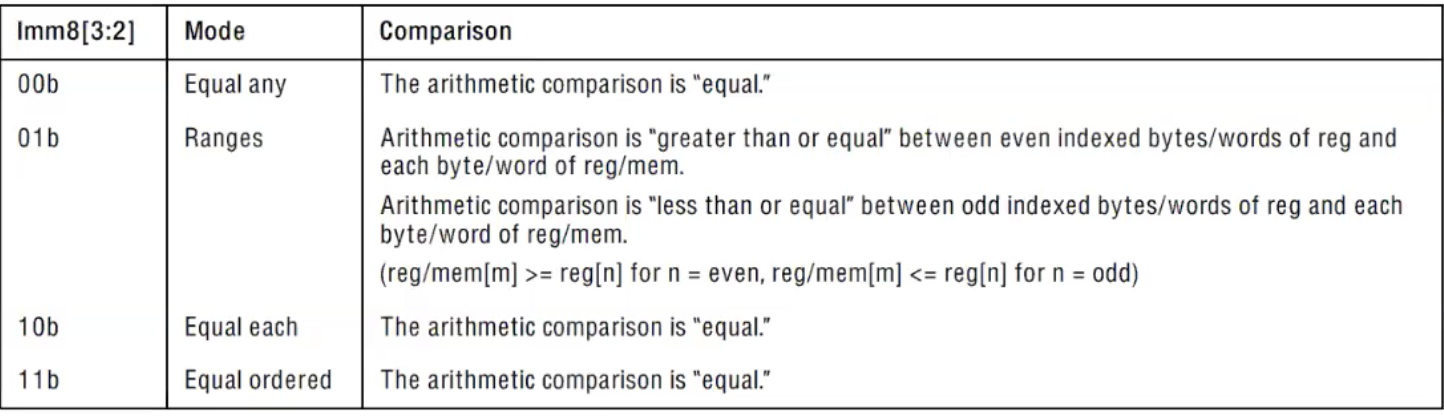
בפסודו קוד כל אחד מהmodes האלה עושה את הבא

ניתן לראות שנעשת בדיקה על הביט ה 0 כדי לדעת כיצד להתייחס לdata מבחינת גדלים.
הביטים ה 4 וה5 הם מניפולציות שאפשר לעשות על index התוצאה במידה והפקודה היא מסוג index ולא mask
הביט ה6 הוא control byte והוא עושה דברים שונים בין אם עובדים עם mask ובין אם אינדקס
1. עבור index - האם האינדקס שחוזר יהיה האינדקס של התו הראשון שמקיים את השיוויון או האחרון.
2. עבור mask הפעולה מחליטה האם התוצאה תהיה בתצורת מספר ששמור ב16 הביטים הראשונים של הרגיסטר או byte spread כלומר כל בית יהיה או FF או 0 במידה והוא מקיים את השיוויון שנקבע מראש או לא

Index result

כפי שאמרנו התוצאה יכולה להיות mask או אינדקס מספרי ב RCX. נדגים איך להשתמש בפקודה ששומרת את התוצאה באינדקס מספרי. למשל חישוב אורך מחרוזת.

section .data
str: db ‘Ab1cDE23f4gHi5J6’
      db ‘Ab1cDE23f4g\0’
EOS_mask: db 0x1,0xFF
	    times 14 db 0
imm: equ 00010100b

section .text
global s
s:
    enter
    xor rax, rax
    xor rcx, rcx
    movdqu xmm1, [EOS_mask]
    .loop
        add rax, rcx
        pcmpistri xmm1, [str+rax], imm
        jnz .loop

    add rax, rcx
    leave
    ret

המחרוזת ארוכה יותר מ16 בתים לכן הקוד משתמש בלולאה.
חובה להשתמש ב implicit length שכן מטרת התוכנית היא חישוב אורך.
נשתמש ב equal range.
כל איטרציה של הלולאה צוברים את הערך של RCX ב RAX עד ש ZF יהיה דלוק.
נשים לב שindex כפי שאמרנו הוא לא בידיוק צובר אלא יכול להחזיר את האינדקס הראשון שדולק או האחרון שדולק, כאן כמובן נחזיר את האחרון כי במקרה הזה הוא מייצג בידיוק את מספר האיברים שקיימו את התנאי שזה גם האורך של המחרוזת.

C Intrinsics

המקבילה של פקודות SSE אבל בשפת c. במדעי המחשב Intrinsics הם בד״כ פונקציות שהמימוש שלהם מטופל על ידי הcompiler. בדומה לפונקציות inline כאשר הקומפילר רואה פונקציה מהסוג הזה הוא מחליף פשוט את הקריאה בקוד של הפונקציה הזמן בזמן קומפילציה. ל C יש Intrinsics שממפים קריאות פונקציה לפקודות SIMD.

מבנה הפקודה הוא מהצורה

_m m <bit width>_<name>_<data type>

bit width הוא מהסוגים הבאים:
data type הוא מהסוגים הבאים:

למשל נסתכל על הפקודה

_mm256d_add_pd(__mm256 a , __mm256 b)

הגודל הוא 256 ביט שמכיל 4 doubles.
הפונקציה היא add
pd - packed double בידיוק כמו ב AVX

את המידע המדויק ניתן לראות בדוקומנטציה של SIMD Intrinsics
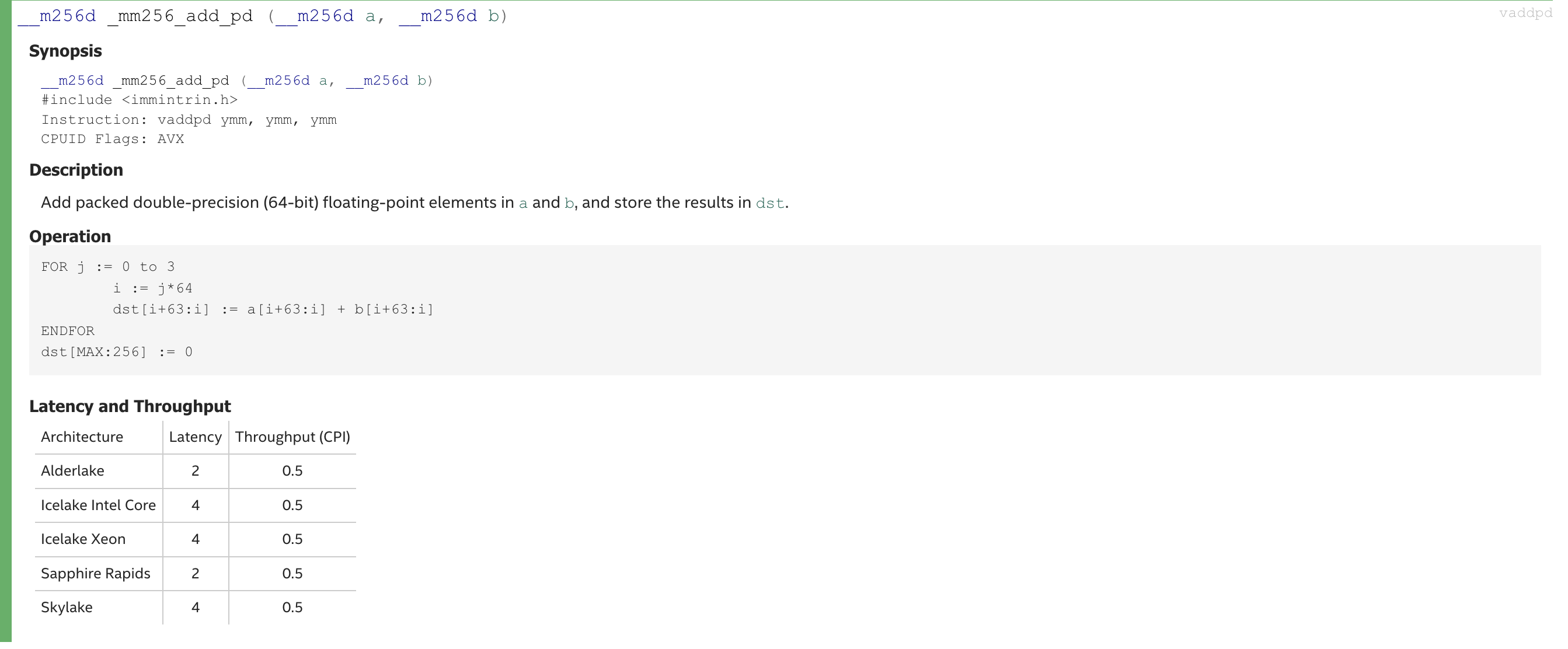
Pasted image 20240330143519.png

נראה קוד c פשוט שמחבר בין שני מערכים מסוג float

float a[8] = {2.0, 4.0, 6.0, 8.0, 10.0, 12.0, 14.0, 16.0};
float b[8] = {1.0, 3.0, 5.0, 7.0, 9.0, 11.0, 13.0, 15.0};
 
  for(int i=0; i<8; i++)
    a[i] = a[i] + b[i];

וכעת נדגים את המקביל אליו באמצעות פקודות SSE בשפת C.

#include <immintrin.h>
#include <stdio.h>
int main() {
 
  /* Initialize input vectors */
  __m256 a = _mm256_set_ps(2.0, 4.0, 6.0, 8.0, 10.0, 12.0, 14.0, 16.0);
  __m256 b = _mm256_set_ps(1.0, 3.0, 5.0, 7.0, 9.0, 11.0, 13.0, 15.0);
 
  /* Call add function */
  __m256 result = _mm256_add_ps(a, b);
 
  /* Display the elements of the result vector */
  float* f = (float*)&result;
  printf("%f %f %f %f %f %f %f %f\n",
    f[0], f[1], f[2], f[3], f[4], f[5], f[6], f[7]);

  return 0;
}

נשים לב לשורה include immintrin.h שמביאה את כל ההרחבות של SSE/AVX בשפת C.
במקום לאתחל מערך של וקטורים אנחנו מאתחלים שני וקטורים מטיפוס mm256__ באמצעות שורת הקוד mm256_set_ps_ (כמובן שלוקטורים בגדלים אחרים עם data type אחרים יש פקודה שקולה).
לאחר מכן השתמשנו בפקודת ה add שהראנו למעלה.
ניתן לראות משהו מעניין, כדי להמיר את התוצאה למערך של float כל מה שצריך זה לתפוס את הפלט מפקודת החיבור ולהמיר את הכתובת שבה הוא נמצא בזכרון לכתובת ל float, בעצם אנחנו ״מפצלים״ את הוקטור לשמונה מספרי float בגודל 32 ביט כל אחד. נשים לב שזה לא אומר ש result עצמו שמור בזכרון, הוא היה יכול להיות שמור גם ב register , אבל כשהקומפיילר רואה את הפקודה הזאת הוא יודע שהוא צריך להעביר את התוכן של result ל ram ולהחזיר כתובת שההסתכלות על התוכן של המידע בכתובת הזאת יהיה כfloat, גם מבחינת גודל וגם מבחינת ייצוג הביטים.

הפלט בהדפסה יהיה:
Pasted image 20240330144406.png
הסיבה שזה בסדר הפוך היא בגלל שהמערכת שבה זה הורץ היא מסוג Little Endian.

נסתכל על דוגמה נוספת

__mm256d_mm256_permute_pd(__mm256 d , int mm8)

הפקודה מקבלת וקטור בגודל 256 ביטים ומספר בקרה mm8.
הפקודה מחזירה שוב וקטור בגודל 256 ביטים שהוא פרמוטציה של הקלט שנקבעת לפי הביטים של מספר הבקרה.
- מספר הבקרה צריך להיות מספר שניתן לייצגו עם 4 ביטים בלבד למשל 0b0101=0x5.
- כל ביט i במספר הבקרה מייצג את העבודה שהפונקציה תעשה עם הdouble ה i בוקטור.
- אם הביט ה i הוא זוגי אז אם הוא כבוי נשים בdst במקום הi את המספר הi בוקטור, אחרת נבצע החלפה, במקום הi של dst נשים את המספר ה i+1 בוקטור הקלט.
- אם הביט הi הוא אי זוגי אז אם הוא כבוי עושים החלפה של וקטור הקלט באינדקס i-1 עם dst באינדקס i ואחרת , אם הביט דלוק מכניסים ל dst במקום הi את וקטור הקלט במקום הi.

למשל עבור השורת קוד vec2 = _mm256_permute_pd(vec2, 0x5) -

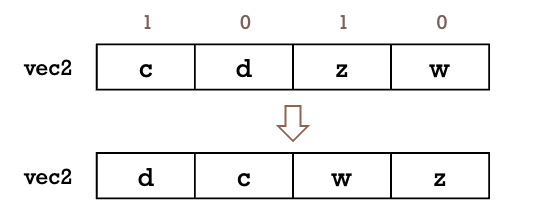
Pasted image 20240330153139.png|350

דוגמה 1
נכתוב תוכנית עם c Intrinsics שמחשבת את האינדקס של ערך מינימלי במערך של 8 floats.

int sse_min_index(unsigned short arr[8]) {
    /* load the elements into a __m128i variable */
    __m128i input = _mm_loadu_si128((__m128i*)arr);

    /* Get the position of the minimum value in the input register */
    __m128i minpos = _mm_minpos_epu16(input);

    /* Extract the position of the minimum value */
    return ((unsigned char*) &minpos)[2];
}

השורה הראשונה לוקחת את המערך מהזכרון וטוענת אותו לטיפוס מסוג m128i כלומר וקטור בגודל 128 ביטים של integers.
1. חשוב לציין שמאחורי הקלעים הטיפוס הנ״ל הוא בסך הכל typedef של long long אבל מאחורי הקלעים בגלל שמדובר ב Intrinsics הקומפיילר יודע שהטיפוס הזה הוא בעצם וקטור xmm/ymm (לפעמים, הקומפיילר יכול להחליט אם לטעון לזכרון או ישירות לוקטור).
minpos - עושה בידיוק את מה שהקוד מבקש, מחזיר את האינדקס המינימלי מבין כל הintegers בגודל 16 ביט.
האינדקס נשמרת בביטים 16-18 כשכל שאר הביטים מאופסים. לכן בשורת ההחזרה נרצה להסתכל אל הפלט בוקטור של תווים ולשלוף את הערך של התו השני.
כדי לקמפל את התוכנית צריך לתת לgcc דגלים שמאפשרים תמיכה בגרסאות ה sse המתאימות, במקרה הזה גרסא 4.1.

דוגמה 2
נרצה לכתוב את xysum שכתבנו מקודם גם בשפת c. בגדול הרעיון הוא אותו הרעיון רק נציג את הקוד ואת הפקודות החדשות שנראה בעקבות הקוד

#include <immintrin.h>

float intrinsics_calc(float x[], float y[], long n) {
    /* Initialize sums */
    __m128 xy_sum = _mm_setzero_ps();
    __m128 x2_sum = _mm_setzero_ps();
    __m128 y2_sum = _mm_setzero_ps();

    for (long i = 0; i < n; i += 4) {
        /* Load 4 floats at a time */
        __m128 x_vec = _mm_load_ps(x + i);
        __m128 y_vec = _mm_load_ps(y + i);

        /* Update vector sums */
        xy_sum = _mm_add_ps(xy_sum, _mm_mul_ps(x_vec, y_vec));
        x2_sum = _mm_add_ps(x2_sum, _mm_mul_ps(x_vec, x_vec));
        y2_sum = _mm_add_ps(y2_sum, _mm_mul_ps(y_vec, y_vec));
    }

    /* Calculate xy sum and convert to float */
    xy_sum = _mm_hadd_ps(xy_sum, xy_sum); // (x1 + x2, x3 + x4, x1 + x2, x3 + x4)
    xy_sum = _mm_hadd_ps(xy_sum, xy_sum); // (x1 + x2 + x3 + x4, x1 + x2 + x3 + x4, x1 + x2 + x3 + x4, x1 + x2 + x3 + x4)
    float xy_sum_float = _mm_cvtss_f32(xy_sum);    

    /* Calculate sqrt(x2_sum + y2_sum) and convert to float */
    __m128 square_sums = _mm_hadd_ps(x2_sum, y2_sum);
    square_sums = _mm_hadd_ps(square_sums, square_sums);
    square_sums = _mm_hadd_ps(square_sums, square_sums);
    
    __m128 square_sums_sqrt = _mm_sqrt_ps(square_sums);
    float square_sums_sqrt_float = _mm_cvtss_f32(square_sums_sqrt);
    
    /* Return xy_sum - sqrt(x2_sum + y2_sum) */
    return xy_sum_float - square_sums_sqrt_float;
}

_mm_setzero_ps מאתחל וקטור של 0
_mm_hadd_ps מבצע horizontal sum שמקבל שני וקטורים x,y ומחשב $x_{i} + y_{i}$ ושם את התוצאה באינדקס המתאים בוקטור חדש.
_mm_cvtss_f32 ממיר וקטור ל single scalar float32 .
_mm_sqrt_ps מבצע שורש על כל איבר בוקטור.