#computer_system #computer_science

ייצוג מספרים שליליים בבינארי

נרצה להבין בנוסף להמרות לבסיס בינארי כיצד ניתן לקבץ אוסף של ביטים כדי לייצג מידע. בפרט עבור מספרים שליליים.

Unsigned

עבור integer word שנסמנה $X$ עם הביטים $(x_{i} | i = 0 \dots w - 1)$ כאשר $w - 1$ מייצג את ה MSB (הביט עם ה״משקל הכי גבוה|) יתקיים

U (X) = \sum_{i = 0}^{w - 1} x_{i} 2^{i}

זה נובע מההמרות שדיברנו עליהם ושניתן לייצג כל מספר כפולינום. הסימון $U (X)$ מייצג את הערך ה unsigned של $X$ בבסיס עשרוני.

Sign & Magnitude

הפתרון הפשוט ביותר עבור $X$ הנ״ל הוא פשוט להגדיר שה MSB הוא ביט סימן. כלומר $1$ לסימון מספר שלילי ו $0$ למספר חיובי. המשמעות היא שאנחנו מפצלים הערכים האפשריים באופן הבא

- (2^{w - 1} - 1), \dots, - 1, - 0, + 0, + 1, \dots, (2^{w - 1} - 1)

החסרון הברור ביותר הוא שצמצמנו את כמות המספרים ויש שני ייצוגים ל $0$ שלא לצורך. באופן כללי הנוסחת המרה תראה כך

M (X) = (1 - 2 x_{w - 1}) \cdot \sum_{i = 0}^{w - 2} x_{i} 2^{i}

כלומר במצב של $x_{w - 1} = 1$ אנחנו פשוט מכפילים את כל שאר הביטים ב $- 1$ . לכן ישנם ייצוגים כפולים. בעיה נוספת שנובעת היא האריתמטיקה של מספרים שמיוצגים באופן הזה כיוון שיש ביט שלא משומש עבור פעולות אריתמטיות אלא רק עבור סימן בלבד.

Two’s Complement

השיטה הנפוצה כיום לייצוג מספרים שלמים שליליים.

המעבר סימן של X יהיה $\neg X + 1$ כלומר נהפוך את הסיביות של המספר ונוסיף $1$ בסוף (התהליך הוא סימטרי גם למעבר מחיובי לשלילי וגם ממעבר משלילי לחיובי).

כדי להמיר את המספר המיוצג לעשרוני נשתמש בנוסחה הבאה.

T (X) = - x_{w - 1} 2^{w - 1} + \sum_{i = 0}^{w - 2} x_{i} 2^{i}

נוסחת ההמרה הזאת בעצם אומרת ״או שה MSB מקבל משקל שלילי וכל השאר רק ״מקטינים את ערכו״ או שהוא לא תורם בכלל.

המשמעות היא כמו במספרים שליליים בעשרוני. המספר שהיה הכי גדול בערך מוחלט יהיה הכי קטן כאשר הוא שלילי למשל עבור בייט בודד מדובר במספר $- 128$

10000000

וכל הוספה של ביטים אליו רק תגדיל אותו לכיוון $0$ למשל

10000001_{2} = - 127_{10}

הבחנה

נוכל לנצל את התכונה הזאת כדי להמיר מספרים המיוצגים בשיטה הזאת די מהר על ידי עבודה עם החזקות. למשל 1001000000100000 יהיה מאוד קשה להמיר בשיטה הנ״ל ולכן נוכל לקחת את $2^{15} = 32768$ ולהחסיר ממנו עבור המקומות בייצוג הנ״ל שעבורם יש $1$ במקרה זה $2^{15}, 2^{5}$ וסך הכל נקבל שבייצוג עשרוני המספר הנ״ל הוא $- 28640$

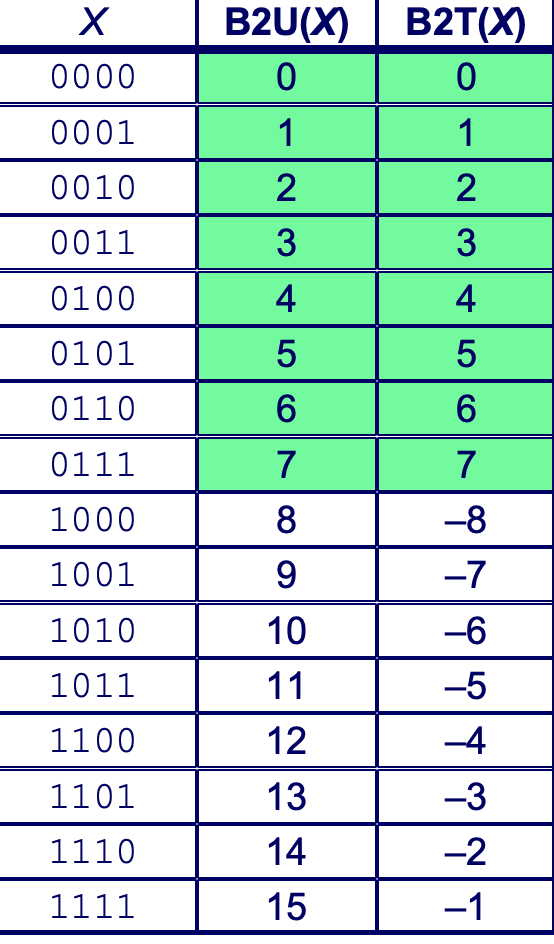
Pasted image 20230212002320.png|200

Numeric Ranges

הסימון עבור הערכים המקסימלים והמינימלים בייצוג כלשהם יהיו

(Sign of represntation) M i n (Sign of represntation) M a x

למשל עבור unsigned יתקיים

U M i n = 0 U m a x = 2^{w} - 1 = 11111 \dots 1

בעוד שעבור המשלים ל2 מתקיים

T M i n = - 2^{w - 1} = 1000 \dots 0 T M a x = 2^{w - 1} - 1 = 01111 \dots 1

נשים לב שבייצוג זה אין שתי ייצוגים ל $0$ אלא ייצוג יחידני והוא $000 \dots 0$ . כמו כן הבחנה חשובה היא ש

| T m i n | = T M a x + 1

כלומר אין סימטריה מלאה בין הערכים. לערך הקטן ביותר במספרים השליליים אין ייצוג חיובי למשל עבור בייט בודד ערך זה יהיה $- 128$ . המשמעות היא שזה המספר היחיד שההמרה שלו מייצוג שלילי לחיובי על פי השיטה שהראנו לא תשנה את ערכו. וגם אם נשנה את אופן ההסתכלות של הייצוג למשל אם נסתכל על אוסף הביטים שמייצגים את המספר הזה בשיטה של unsigned , נשמח לגלות שזה המספר היחיד שסימנו מתחלף וערכו הוא פשוט ערכו בערך מוחלט.

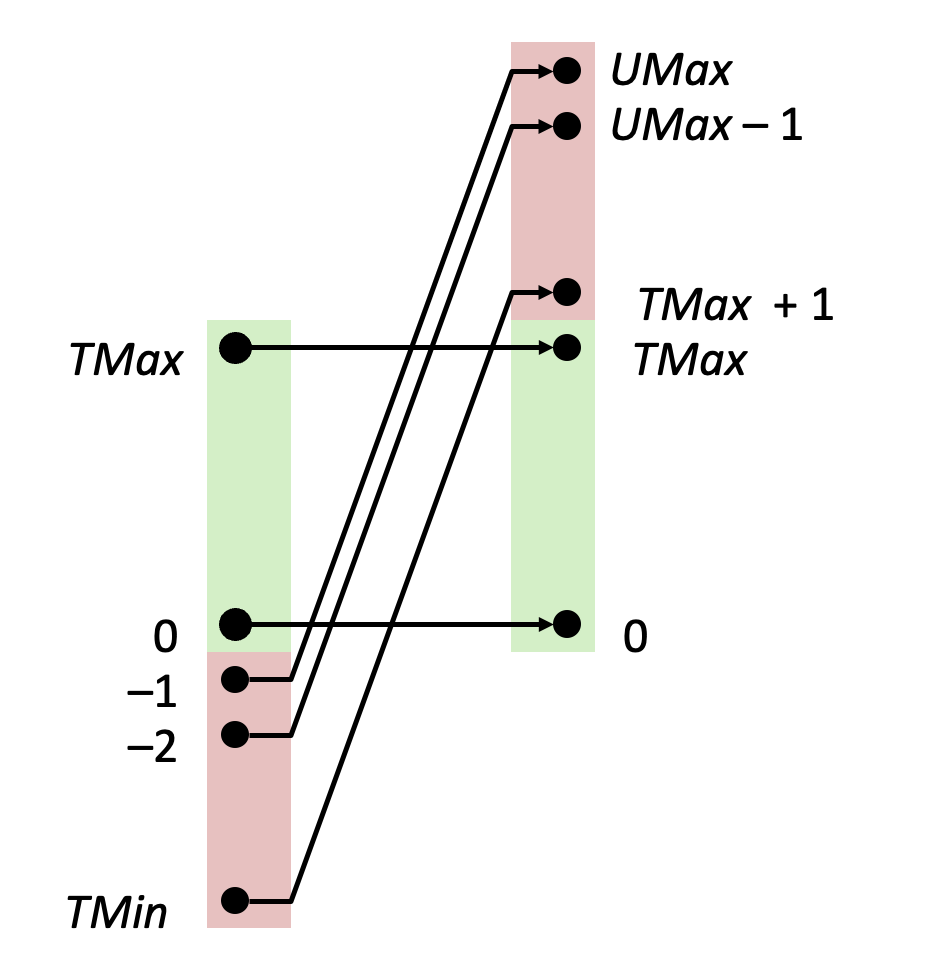
Pasted image 20230212002414.png|250
נוכל לראות אם כן שהערך המקסימלי ביותר ב $U$ הוא $2 T M a x$

Casting Signed to Unsigned

בשפת $c$ ניתן תמיד להמיר בין שני הייצוגים על ידי explicit casting

short int x = -15213;
unsigned short int ux = (unsigned short) x;

משמעות ההמרה היא באופן ההסתכלות על הייצוג של המספר, כלומר אם המרנו מספר שלילי למספר חיובי הרי שערכו הולך לגדול מהתמונה למעלה.

סימון מספרים unsigned

נהוג לסמן מספרי unsigned עם suffix של U למשל 429496U.

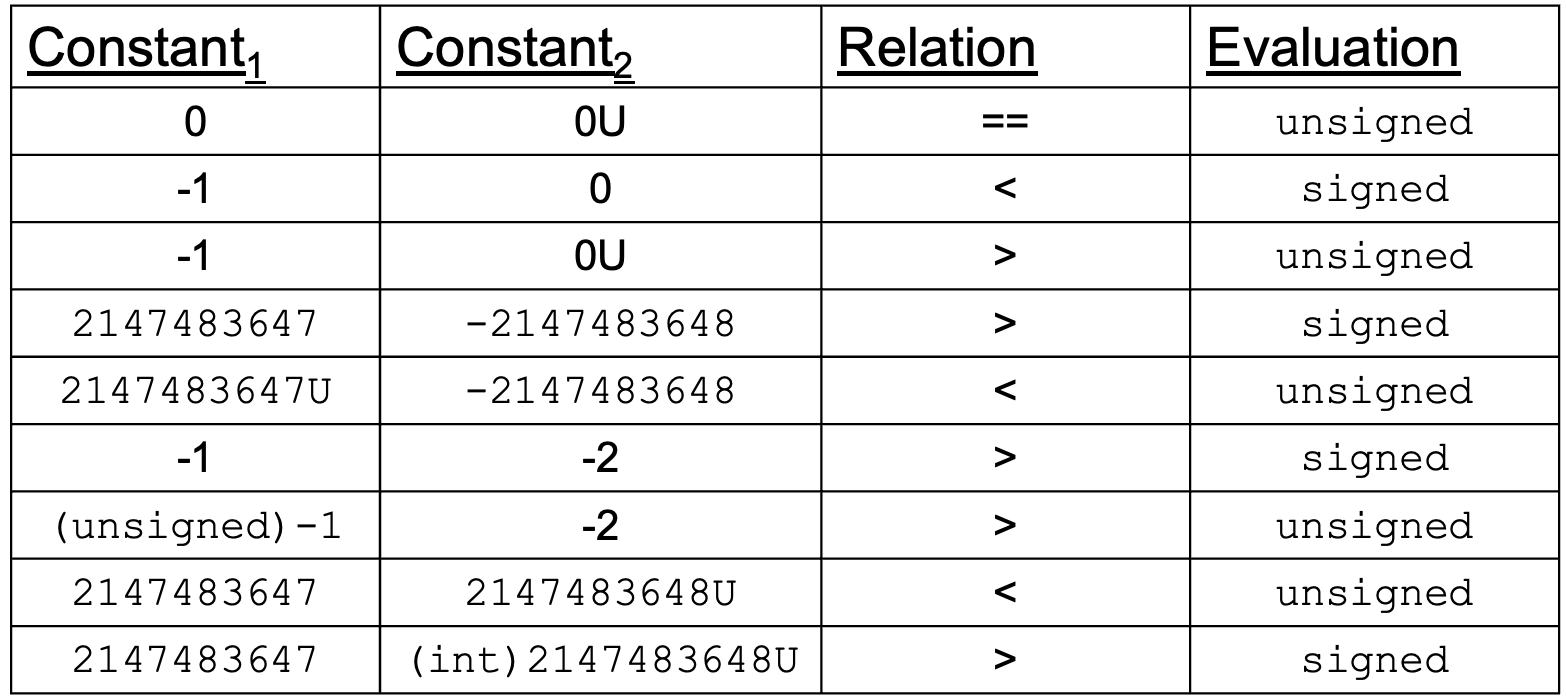
Casting Surprises

נשים לב שבהינתן שמשלבים באותו ביטוי ובפרט ביטוי בוליאני מספר ללא סימן ומספר עם סימן תמיד תהיה המרה למספר ללא סימן וזה יכול להשפיע על נכונות הביטויים.

Pasted image 20230212003308.png|350

Sign extension

כאשר ננסה להמיר מספרים מגודל קטן יותר לגודל גדול יותר הקומפיילר ידעת להרחיב את הסימן באופן אוטומטי. הקומפיילר מעורב בתהליך הזה כיוון שלאחר שלב הקומפילצייה המידע מנוהל כבר כסדרות של ביטים ולכן יש חשיבות לריפוד הזה בשלב הקימפול.

א) אם מדובר ב unsigned value אז הריפוד יהיה ב $0$ .
ב) אם מדובר ב signed value אז הריפוד יהיה לפי ה MSB.

Warning

נשים לב שאם אנחנו נבצע הרחבת סימן ולאחר מכן נבצע פעולות שמכילות גם unsigned וגם signed value הדבר עלול להשפיע על הערך שעבורו בוצעה הרחבת הסימן אם מדובר במספר שלילי, כאשר הוא יומר למספר ללא סימן ערכו יגדל משמעותית

חיבור

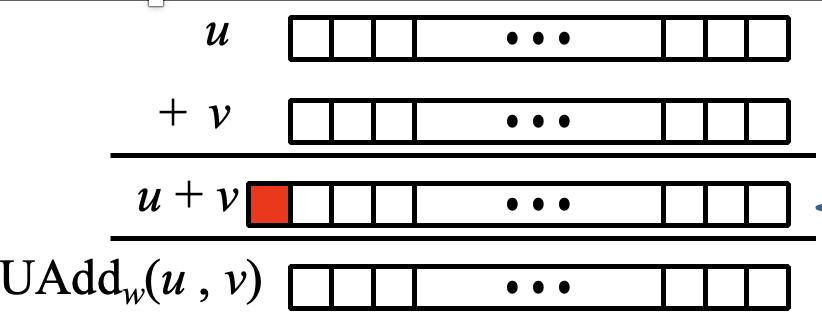
unsigned
נגדיר את החיבור של שתי מספרים ללא סימן $u, v$ להיות

U A d d_{w} (u, v) = u + v m o d 2^{w}

נוכל גם להגדיר זאת כך

u + v = {\begin{cases} u + v & u + v < 2^{w} \\ u + v - 2^{w} & 2^{w} \leq u + v < 2^{w + 1} overflow \end{cases}

המשמעות היא פשוט התעלמות מה carry במידה והוא עבר את ה msb . כלומר אם נחבר מספרים שיוצאים מהטווח נקבל overflow ונבצע פעולת מודולו עם הערך המקסימלי כדי לדעת מה המספר הרצוי.

הבחנה

עבור $x, y$ מספרים ב signed ו $u x, u y$ ההמרה שלהם לunsigned מתקיים

u x + u y == x + y $ $ ז ה ת מ י ד T r u e

Pasted image 20230212004759.png|250

Two’s Complement Addition
נגדיר את החיבור של שתי מספרים עם סימן $u, v$ להיות

u + v = {\begin{cases} u + v - 2^{w} & 2^{w - 1} \leq u + v positive overflow \\ u + v & - 2^{w - 1} \leq u + v < 2^{w - 1} \\ 2^{w} + u + v & u + v < - 2^{w - 1} negative overflow \end{cases}

הכפל

נגדיר את הכפל עבור מספרים ללא סימן $u, v$ להיות $U M u l t_{w} (u, v) = u v m o d 2^{w}$
עבור מספרים עם סימן נבצע את הפעולה הנ״ל ולאחר מכן נמיר לפי שיטת ההמרה שהצגנו (הפיכת הסימון והוספת 1)