#computational_models #computer_science

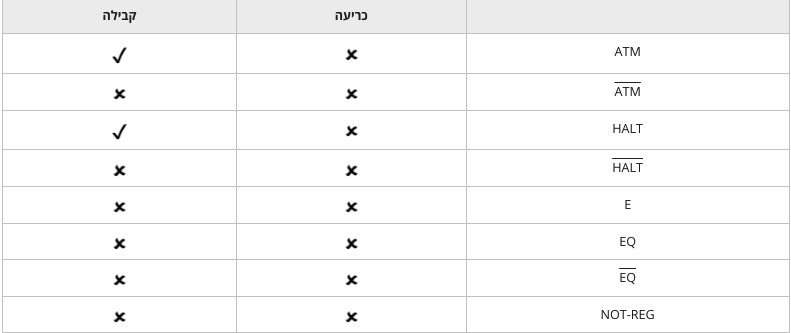
אי כריעות

אימות תוכנה והשפה ATM

A T M = {(P, w) | P (w) = 1}

כך ש:

P הוא קוד תקין של תוכנית
w מחרוזת
מתקיים שאם מריצים את המחרוזת על התוכנית נקבל פלט חזרה 1.

התוכנה האוניברסלית U

התוכנה U היא תוכנה שמקבלת כקלט זוג מחרוזות P, w, ופועלת כך:

מריצה את התוכנה P על הקלט w (במקרה שבו P אינה תוכנית מחשב תקינה אז U מחזירה ערך 0).
U מחזירה את ערך החזרה שהתקבל מהריצה של P על w.
נשים לב שאם P לא עוצרת על w אז גם U לא עוצרת על הזוג (P,w). התוכנה U פועלת באופן דומה לאופן שבה מערכת ההפעלה מפעילה תוכנות אחרות.
התוכנה U נקראת גם "תוכנה אוניברסלית" (או, בעולם מכונות הטיורינג "מכונת טיורינג אוניברסלית") כיוון שהיא תוכנה אחת שיכולה לתת התנהגות כמו כל תוכנה אחרת.

ניתן להוכיח ש ATM קבילה עם U

(P, w) \in A T M \leftrightarrow P (w) = 1 \leftrightarrow U (P, w) = 1

נשים לב, U היא תוכנה, אין צורך להוכיח שהיא שקולה למכונה כלשהי כי כבר הראנו שכל תוכנה שקולה למכונת טיורינג. השפה המכונה הזו מקבל היא השפה ATM כלומר כל זוג בשפה מגיע למצב מקבל. לעומת זאת כל זוג שאינו בשפה יכול לגרום ל U לא לעצור. זה תלוי בתוכנה עצמה שהיא חלק מהזוג הסדור

השפה ATM לא כריעה

נניח בשלילה ש ATM כריעה, נסמן D-ATM התוכנית שמכריעה את השפה. נרשום את התוכנית

stupid(z) {
  return(!D-ATM(z,z))
}

כעת נחלק למקרים עבור הקריאה ל stupid(stupid) :
1)

אם ערך החזרה הוא 1 נקבל שהזוג הסדור (stupid,stupid) שייף ל ATM
זה אומר ש D-ATM מחזיר 1
אבל אם כך stupid(stupid)=0 בסתירה

אם ערך החזרה הוא 0 נקבל באופן דומה ש stupid(stupid)=1 בסתירה

מסקנה מצאנו שפה שלא ניתנת להכרעה בעזרת מחשב....

שפה שאינה קבילה $\overset{―}{A T M}$

נניח בשלילה ש $\overset{―}{A T M}$ , שפה קבילה. נקבל ש ATM והמשלים שלה שפות קבילות ולכן לפי משפט היא אמורה להיות כריעה. בסתירה .

בעיית העצירה

H A L T = {(P, w) | P (w) ↓}

במילים, השפה halt הינה שפה של זוגות , תוכנית ומחרוזת כך שהפעלת התוכנית על המחרוזת , עוצרת. (חץ למטה מסמל עצירה חץ למעלה מסמל אי עצירה).

HALT אינה כריעה
נניח בשלילה שהיא כן , אז קיימת תוכנית D-HALT המכריעה אותה

D-HALT(Q,y){...}

D-ATM(P,w) {
 if (D-HALT(P,w)==0) {
  return 0;
 }
 return (U(P,w));
}

בעצם הצלחנו עכשיו להכריע את השפה ATM כי קיבלנו את הידע של ״האם התוכנית עוצרת או לא״
אם התוכנית לא עוצרת אז אנחנו יודעים להכריע את המצב הזה כעת ולהחזיר 0 כאילו D-ATM דוחה מצבים כאלה, אחרת התוכנית עוצרת בוודאות ונוכל להריץ את מכונת הטיורינג האוניברסלית ולקבל תשובה. בסתירה לכך שהפה ATM כריעה.

HALT קבילה

A-HALT(Q,y) {
 U(Q,y)
 return (1);
}

קל להבין למה התוכנית מקבלת את השפה . אם U עוצרת נחזיר 1 אחרת היא לעולם לא תעצור או תחזיר 0, אין לנו איך לדעת .

השפה E

E = {P | L (P) = \emptyset}

כלומר שהשפה של P ריקה. המשמעות היא שלכל קלט התוכנית לא תחזיר 1 , או שהיא תחזיר 0 או שלא תעצור בכלל .

E לא כריעה
נב״ש שקיימת תוכנית שמכריע את E. D-E(Q).

   _
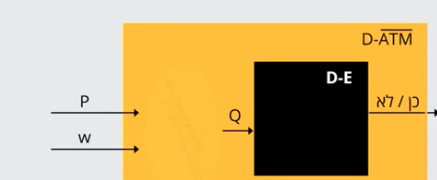
D-ATM(P,w) {
  Q= "Q(x){
    return U(P,w)
  }"
  return D-E(Q)
}

באופן הזה יתקיים

L (Q) = {\begin{cases} Σ^{*} & P (w) = 1 \\ \emptyset & P (w) \neq 1 \end{cases}

כלומר $Q \in E \leftrightarrow P (w) \in \overset{―}{A T M}$ . למה בעצם? הגדרנו את Q באופן כזה שאין תלות בקלט של Q אלה בקלט של השפה המכריעה את המשלים ל ATM. מה שזה אומר בעצם ש מה שתוכנה D-ATM מחזירה היא בידיוק הכרעה לבעייה שלה. בסתירה לכך שניתן להכריע אותה

זה בעצם המטרה שלנו, לקחת תוכנית לא כריעה אחרת ולהצליח להכריע אותה על ידי שפה שהנחנו שהיא כריעה. אנחנו נרצה להעזר בקופסה השחורה הזאת של D-E או של כל בחירה אחרת, כדי להצליח להכריע את הקלט של השפה האחרת במקרה זה D-ATM משלים. מה שאנחנו עושים בעצם זה רידוקצייה (אפרט בהמשך) על הקלט הראשון, ממירים אותו לקלט של התוכנית השנייה באופן כזה שיעזור לנו להכריע את התוכנית הראשונה.

Pasted image 20220711192132.png

E לא קבילה
נוכיח ש $\overset{―}{E}$ קבילה כי אז בהכרח E לא קבילה אחרת היא תהיה כריעה בסתירה.

A-EC(Q) {
 guess(w)
 return U(Q,w)
}

EC זה E משלים (סימון נוסף)

מנחשים מחרוזת ומריצים את המחרוזת על תוכנית הקלט. יכול להיות שהיא תקבל ויכול להיות שהיא תדחה , וגם יכול להיות שהיא לא תעצור. לכן מדובר בקבלה.

השפה EQ

E Q = {(P_{1}, P_{2}) | L (P_{1}) = L (P_{2})}

EQ אינה קבילה

A-E(P) {
 Q1=P
 Q2= "Q(x){return(0)}"
return A-EQ(Q1,Q2)
}

כעת יתקיים

ֿ L (Q_{2}) = \emptyset

ולכן

A-EQ(Q1,Q2) return 1 \leftrightarrow (Q_{1}, Q_{2}) \in E Q \leftrightarrow L (P) = \emptyset \leftrightarrow A-E(P) return 1

כלומר הראנו ש A-EQ מחזירה בידיוק מה שצריך כדי לקבל את A-E . כלומר הצלחנו לבנות תוכנית המקבלת את E בסתירה לכך שהיא קבילה

אם היא לא קבילה אז היא בהכרח גם לא כריעה.

האפשרות של שפת המשלים היא אם כן , שהיא תהיה קבילה בלבד. לא ייתכן שהיא תהיה כריעה. לא אוכיח זאת פה אבל זאת שפה שאינה כריעה.ֿ

רדוקצייה

תכלס, זה מה שעשינו עד עכשיו. אבל נסביר מה זה רדוקצייה באופן מפורש. מטרת הרידוקצייה היא לפתור בעיה אחת באמצעות בעייה אחרת. באופן פורמלי יותר.
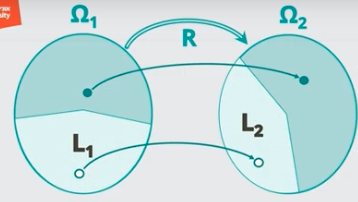
Pasted image 20220711195759.png
רידוקצייה היא בעצם פונקציית המרה.

בהינתן $L_{1, 2} \subseteq Ω_{1, 2}$ , רידוקציית התאמה היא פונקצייה $R : Ω_{1} \to Ω_{2}$ כך ש:

\forall_{x \in Ω_{1}} : x \in L_{1} \leftrightarrow R (x) \in L_{2}

סימון : אם קיימת רידוקציית התאמה חישובית מ $L_{1}$ ל $L_{2}$ מסמנים : $L_{1} ⪯_{m} L_{2}$ .

טענה : תהיינה שתי שפות $L_{1, 2}$ אם

$L_{2}$ כריעה
$L_{1} ⪯_{m} L_{2}$

אזי $L_{1}$ כריעה.

הוכחה

D-L1(x) {
 return D-L2(R(x)) 
}

בהינתן קלט מ $x \in Ω_{1}$ . נשים לב שהרידוקצייה צריכה להיות מחושבת על ידי הכלים שאנחנו מכירים. R מייצגת בעצם תוכנית כמו שעשינו ב E . התוכנית הזאת תאפשר לנו להמיר קלט של תוכנית המכריעה שפה אחת לקלט של תוכנית המכריעה שפה אחרת ואז להשתמש ב ״קופסה השחורה״ שדיברנו עליה.

אנחנו עשינו זאת בדרך השלילה... כלומר
Pasted image 20220711201010.png

רדוקציה חישובית משפה כריעה ל ATM

הוכחה תהי $A$ שפה כריעה, התוכנית המכריעה אותה היא D-A. נגדיר את פונקצית הרידוקצייה

R(w){
 if D-A(w)==1 {
  return "Q(A){return 1}, abba"
 } 
 return "Q(A){return 0}, abba"
}

קל לראות שזאת רידוקצייה חישובית, והיא תמיד עוצרת. כמו כן הפלט תמיד יהיה שייך ל ATM אם הקלט שייך ל A.

נשים לב, קיימת רידוקצייה חישובית משפה כריעה לכל שפה פרט לשפה הריקה ו $Σ^{*}$

השפה NOT-REG

NOT-REG = {Q | L (Q) is not regular}

כל התוכניות שהשפה שמקבלת אותן אינה רגולרית.

נוכיח שזאת שפה שאינה כריעה
נוכיח שיש רידוקציית התאמה חישובית בין לשפה לא כריעה ל not-reg נבחר את HALT.
יתקיים $Ω_{1} = {(P, w)}$ , $Ω_{2} = {Q}$ .

כעת נרצה ליצור פונקצייה $R$ שתקבל זוג של תוכנית ומחרוזת ותחזיר תוכנית אחרת Q כך ש

Q \in NOT-REG \leftrightarrow (P, w) \in HALT

כלומר

L (Q) is not regular \leftrightarrow P (w) ↓

R(P,w) {
  "Q(x) {
    U(P,w)
    return Palindrom(x)
  }"
}

נשים לב ש R לא מחשבת את Q היא רק מייצרת אותו
מה עשינו כאן בעצם? יצרנו פונקצייה שבשלב הראשון מריצה את המכונה האוניברסלית על התוכנית עם המחרוזת. אם היא לא עוצרת אז השפה המקבלת את Q היא השפה הריקה שהיא רגולרית. אחרת זאת שפת הפלינדרום שהיא לא רגולרית.

כנדרש .

נוכיח שזאת שפה שאינה קבילה
כעת לפי המתכון צריך לבצע רידקוצייה משפה אחרת שאינה כבילה. נבנה רידוקצייה מ $\overset{―}{A T M}$ .
הרידוקצייה תקבל זוג סדור של תוכנית ומחרוזת , ותבנה מחרוזת אחרת שמייצגת תוכנית שתקיים שהזוג יהיה שייך ל ATM משלים אם ורק אם התוכנית שהרידוקצייה תחזיר תיהיה שייכת ל NOT-REG.

נוכל לבנות את הקוד הבא

R(P,w) {
  "Q(x) {
    if Palindrom(x) {return 1}
    return U(P,w)
  }"
}

כאן קודם בדקנו אם הקלט הוא פלינדרום כי אם כן אז המחרוזת שייכת לשפה שאינה רגולרית. מה שיקרה כאן בעצם זה שאם P(w) שווה ל1 אז הקלט לא משנה, בין אם הוא פלינדרום ובין אם לא לכן השפה תהיה כל המחרוזות. אחרת השפה תהיה שפת הפולינדרום. כלומר רק אם P(w) נדחה או לא עוצר, נקבל שהשפה של Q היא שפת הפלינדרום כדרוש כי זאת שפה שאינה רגולרית.

Pasted image 20220711204821.png