#computational_models #computer_science

שפות רגולריות

ראשית נזכיר כמה תכונות הנוגעות לשפות רגולריות.
בכלל, שפה $L$ תקרא רגולרית אם קיים אוטומט סופי $A$ המקבל אותה.

הדוגמה הפשוטה ביותר לשפה רגולרית היא השפה הריקה. כיוון שכל אוטומט סופי דטרמיניסטי חסר מצבים מקבלים יתאר אותה.
גם השפה המכילה את המילה הריקה בלבד היא רגולרית (כמו שאמרנו מספיק אוטומט עם מצב התחלתי שהוא גם מקבל).

סגירויות

השפות הרגולריות סגורות ל

שרשור
חיתוך
איחוד
משלים
סגור קלין
reverse (ההוכחה פשוטה, פשוט הוכפים את כל המצבים המקבלים ההתחלתיים והמעברים)
prefix

תזכורת מה זה prefix ,suffix , postfix :

\begin{matrix} prefix(L) = {x \in Σ^{*} | \exists_{y \in Σ^{*}} : x y \in L} \\ suffix(L) = {y \in Σ^{*} | \exists_{x \in Σ^{*}} : x y \in L} \\ sub(L) = {y \in Σ^{*} | \exists_{x, z \in Σ^{*}} : x y z \in L} \end{matrix}

ביטוי רגולרי

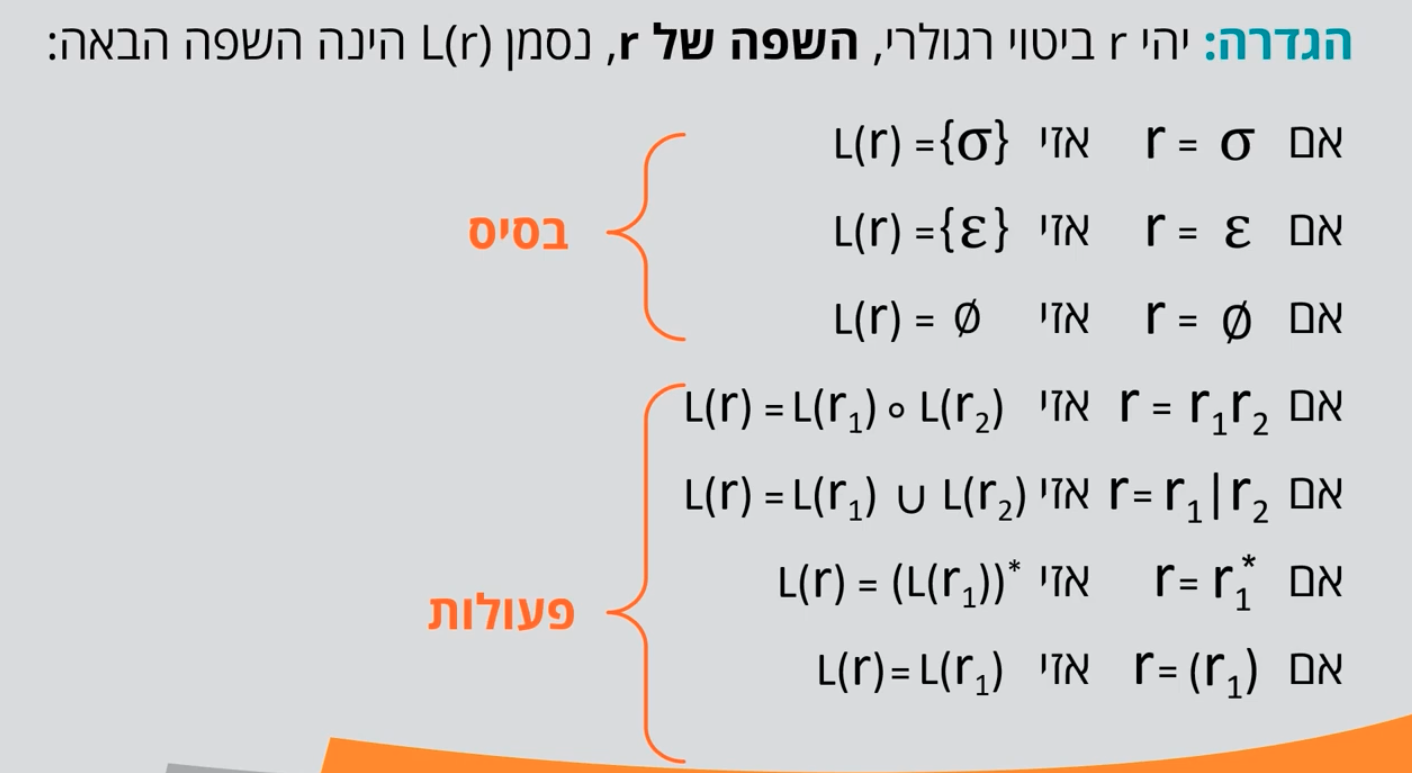
דרך נוספת לתאר שפה רגולרית. מחרוזת תהיה ביטוי ריגולרי אם היא אחת מהצורות הבאות

בסיס האינדוקצייה

$σ$ אות בודדת
$ε$ המחרוזת הריקה
$\emptyset$ הקבוצה הריקה

פעולות האינדוקצייה בהינתן $r_{1}, r_{2}$ ביטויים רגולרים

$r_{1} r_{2}$
$r_{1} | r_{2}$
$r_{1}^{*}$
$(r_{1})$

סדר פעולות :

סוגריים
כוכבית
שרשור
איחוד
משמאל לימין

Pasted image 20220710120803.png

שקילות
$L$ רגולרית אם ורק אם ישנו ביטוי רגולרי $r$ כך ש $L = L (r)$ .
ההוכחה של זה בכיוון הראשון (שישנו ביטוי רגולרי $r$ ...) מבוצעת באינדוקצייה על אורך הביטוי $r$ .
ההוכחה בכיוון השני קצת יותר מורכבת :

לשם כך צריך לבנות אוטומט סופי מוכלל שזה אוטומט סופי המאפשר שהמעברים יהיו ביטויים רגולרים. (זה אפשרי באוטומט סופי לא דטרמינסטי).

הדרישות לאוטומט סופי מוכלל :

מצב מקבל יחיד בלי יציאות ומצב התחלתי יחיד בלי יציאות.
קשת בין כל שני קודקודים, כולל קשתות עצמיות, המסומנות בביטויים רגולרים.

האלגוריתם המרה יעבוד באופן הבא

הוספת מצב התחלתי ומצב מקבל חדש המחובר למצבים הישנים על ידי מעברי אפסילון
השלמת כל המעברים החסרים על ידי מעבר של $\emptyset$ (אפשר להפתר מהמעברים האלה זה רק עניין פורמלי)
בניית מעברים ישירים בין מצבים שיש בינהם מספר מעברים, מבוססי ביטויים רגולרים. אחרי שעשינו זאת נמחק את כל מצבי הביניים
נמשיך כל עד למחיקת כל המצבים חוץ מהמצב ההתחלתי והמצב המקבל.

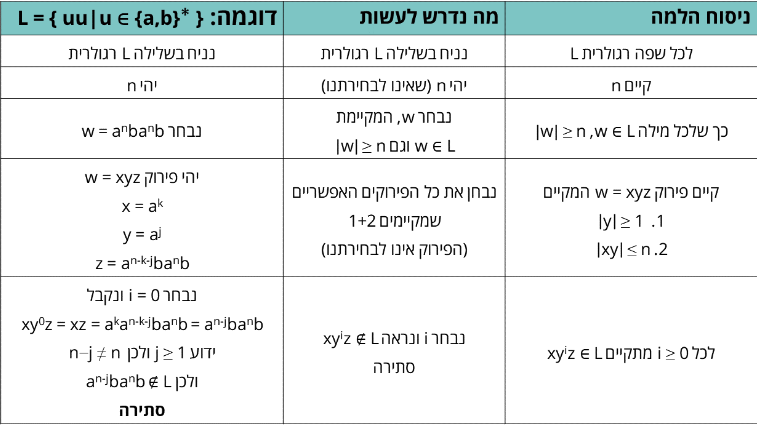
למת הניפוח לשפות רגולריות

אם $L$ שפה רגולרית אז קיים קבוע $N$ כך לשכל $w \in L$ שמקיימת $# w \geq N$ קיימת חלוקה של $w$ לתתי המילים $x, y, z \in Σ^{*}$ כך ש $w = x y z$ ומתקיימים התנאים:

$| y | > 0$
$| x y | \leq N$
$\forall_{i \in N} : x y^{i} z \in L$

נשים לב שזה לא תנאי הכרחי ומספיק כלומר אם שפה רגולרית היא תקיים את זה אבל יכולות להיות שפות לא רגולריות שמקיימות את זה גם כן.
לכן השימוש בלמת הניפוח יבוא לידי ביטוי בעיקר בהוכחה ששפה אינה רגולרית.

Pasted image 20220710164516.png

ניתן להשתמש גם בתכונות הסגירות כדי להפריך ששפה אינה רגולרית.