האינטגרל

האינטגרל המסויים

האינטגרל המסויים של פונקצייה ממשית בקטע $[a,b]$ הוא מספר המתאר את השטח הכלוא בין גרף הפונקצייה לציר ה $x$ בקטע זה. הגדרת האינטגרל באה במקור מהצורך לפתור בעיה גאומטרית אבל בפועל , במובן מסויים , חישוב האינטגרל הוא הפעולה ההפוכה לגזירה, חישוב הפונקצייה הקדומה . זה תוכנו של אחד המשפטים החשובים בנושא האינטגרלים, המשפט היסודי של החשבון האינפיטסמילי. משפט זה מאפשר לחשב את האינטגרל המסויים של פונקציה $f$ בתנאי שיודעים למצוא פונקצייה $F$ המקיימת $F^{\prime }=f$ .
הפונקצייה $F$ נקראת הקדומה של $f$ או האינטגרל הלא מסויים של $F$.

ישנן שתי גישות לתיאור האינטגרל וההגדרה אפרט את שניהן (אומנם לא בהרחבה אבל חשוב להכיר).

האינטגרל המסויים לפי דרבו

תהי $f$ פונקצייה אי שלילית, ממשית , וחסומה (נשים לב שחסומה לא אומר בהכרח רציפה, אך היא בהכרח אומרת שאין נקודות אי רציפות מסוג עיקרי) המוגדרת בקטע $[a,b]$. ויהי $D$ התחום הכלוא בין ציר ה$x$ לגרף הפונקצייה בקטע. למשל:

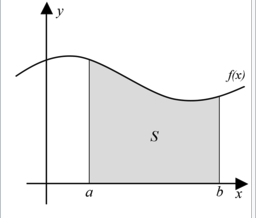
נרצה לחשב את השטח של $S$. או ליתר דיוק להגדיר מספר ממשי $s(S)$ שמתאר את השטח הזה. על פניו מושג השטח נשמע די פשוט, אבל לרוב אנחנו לא יודעים לחשב שטחים בצורה אינטואיטיבית, פרט לצורות השטח הברורות ביותר (משולשים, ריבועים, שטחים וכו). כדי שנתחיל בכלל להגדיר את האינטגרל נרצה לתת הגדרה למושג נוסף.
חלוקה של קטע - סדרה סופית של נקודות $a=x_0<x_1<\cdots <x_n=b$ נקראת חלוקה של $[a,b]$. חלוקה כזאת ניתן לתאר כ $n$ תתי קטעים $[x_0,x_1],[x_1,x_2],\dots ,[x_{n-1},x_n]$ החותכים זה את זה רק בנקודות הקצה שלהם.
נוכל לסמן אורך בודד של קטע $i$ בחלוקה כ $\mathrm{\Delta }{x}_i=x_i-x_{i-1}$ .
כעת נגדיר :
קוטר חלוקה - לכל חלוקה $P$ ניתן להגדיר קוטר חלוקה באופן הבא $\lambda (P)=\underset{i\in [n]}{max}\mathrm{\Delta }{x}_i$
יתקיימו מספר דברים-

1. סכום אורכי הקטעים הוא $\sum _{i=1}^n\mathrm{\Delta }{x}_i=b-a$
2. הקוטר של חלוקה בין קטעים הוא לכל הפחות $\frac{a-b}{n}$
   שים לב לתכונה המעניינת הבאה. עבור החסם התחתום של $f$ , נסמנו $m$ והחסם העליון של $f$ נסמנו $M$ יתקיים שהמלבן שגובהו הוא החסם העליון ובסיסו הוא סכום אורכי הקטעים, מכיל בתוכו את $s(S)$ ואם הגובה הוא החסם התחתון אז הוא מוכל ב $s(S)$. כלומר

(אם הפונקצייה אינה אי שלילית, מסתכלים על השטח מתחת לציר האיקס בסימן שלילי, כלומר מחשבים כאילו היא הייתה מעל ציר הx באותו אופן ומחליפים סימן).

כעת נוכל לבצע תהליך דומה עבור כל תת קטע $[x_{i-1},x_i]$ נסמן את החסם התחתון ב $m_i$ ואת חסם העליון ב $M(i)$ . ולכן תת קטע יתקיים אותו אי שיוויון הנ״ל

נגדיר כעת את המושגים הבאים :
הסכום התחתון - $\underset{―}{s}(f,P)=\sum _{i=1}^n{m}_i\mathrm{\Delta }{x}_i$
הסכום העליון - $\bar{s}(f,P)=\sum _{i=1}^n{M}_i\mathrm{\Delta }{x}_i$
וכמובן שבאופן מיידי מתקיים שהסכום התחתום קטן או שווה מהסכום העליון.

כעת נגדיר את קבוצת כל הסכומים התחתונים עבור כל חלוקה $P$ אפשרית כ

ובאופן דומה קבוצת כל הסכומים העליון עבור כל חלוקה $P$ אפשרית כ

כעת , יתקיים שפונקצייה $f$ היא אינטגרבילית ב $[a,b]$ אמ״מ היא מוגדרת וחסומה שם וגם מתקיים

הערך המשותף הוא האינטגרל עצמו ומסומן כ ${\int }_a^{b}f(x)dx$ כאשר $dx$ מסמן את המשתנה של הפונקצייה שעליו מבצעים אינטגרצייה.

נשים לב לשקילות הטענות הבאות

1. $f$ אינטגרבילית ב $[a,b]$
2. לכל $\epsilon >0$ קיימת חלוקה $P$ של $[a,b]$ כך ש- $\bar{s}(f,P)-\underset{―}{s}(f,P)<\epsilon$ .
3. קיימת סדרה חלוקות $(P_n{)}_{n=1}^{\mathrm{\infty }}$ של $[a,b]$ כך ש:

ניתן לפתח את זה עוד ולהגדיר במפורש מהו פרמטר החלוקה, כיצד הוא מושפע מפונקצייה שהיא אינטגרבילית ומה הקשר בינהם וכו . אומנם אין צורך לפתח את זה בסיכום הזה, בסופו של דבר נגיע להגדרה של פרמטר החלוקה שנשתמש בה ב #האינטגרל המסויים לפי רימן.

האינטגרל המסויים לפי רימן

זאת ההגדרה המוקדמת יותר מבחינה היסטורית. ההגדרה הזאת מתבססת על סכומי רימן
עבור פונקצייה חסומה ב $[a,b]$. וחלוקה $P=\{x_1,x_2,x_3\dots ,x_n\}$. בחירת נקודות עבור $P$ היא סדרה $c=(c_i{)}_{i=1}^n$ כך ש $c_i\in [x_{i-1},x_i]$ .
סכום רימן של $f$ ביחס לחלוקה $P$ ובחירת הנקודות $c$ הוא המספר

כלומר $f(c_i)$  מייצג את גובה המלבן שבסיסו הוא ההפרש האיבר המינימלי והמקסימלי בתת הקטע בחלוקה. נשים לב שסכום רימן הוא סכום כל המלבנים.

כעת, בהינתן חלוקה $P$ נסמן ב $\lambda (P)$ את פרמטר החלוקה - $max(\mathrm{\Delta }{x}_i{)}_{i=1}^n$ .

כעת, נאמר ש $f$ אינטגרבילית (לפי רימן) אמ״מ :
לכל סדרת חלוקות $\{P_m\}$ המקיימת $\lambda (P_m)\to 0$ ולכל בחירת נקודות $\{c_m\}$, סכומי רימן שואפים לאותו גבול. במצב זה הגבול הוא האינטגרל המסויים של הפונקצייה:

נשים לב הדרישה היא שכל הסדרות חלוקה ישאפו לשם, לכן ניתן להפריך אינטגרביליות על ידי מציאת שתי חלוקות המקיימות שפרמטר החלוקה שלהן שואף ל0, שאינן שואפות לאותו מקום. או בהינתן פונקצייה שאנחנו יודעים שהיא אינטגרבילית, נוכל לבחור איזה חלוקה שנרצה (גם חלוקה שווה) ולחשב את הגבול.

כמו כן נשים לב שאם החלוקה שבחרנו שווה, נוכל לנצל את כי $(n\to \mathrm{\infty })\leftrightarrow (\lambda \to 0)$ .

חשוב, לא אוכיח זאת אבל ההגדרות לאינטגרל, לפי רימן או דרבו הן שקולות אחת לשנייה .

חישוב גבולות לפי סכומי רימן

ניתן להעזר בסכומי רימן כדי לחשב גבולות שעם הכלים של אינפי 1 היינו מתקשים לחשב.

• נתמקד בעיקר בקטע $[0,1]$ , בחלוקה שווה, ובבחירה של נקודות ימניות. במצב זה יתקיים

למשל:

כעת נשים לב שמתקיים

כעת נוכל להגדיר $f(x)=\frac{1}{1+x}$ ויתקיים ש $f(\frac{n}{k})$ ייתן בידיוק את הביטוי למעלה, כלומר :

משפחות של פונקציות אינטגרביליות

• אם $f$ רציפה על $[a,b]$ אז היא אינטגרבילית שם.
• אם $f$ מונוטונית וחסומה על קטע $[a,b]$ אז היא אינטגרבילית שם.
• אם $f$ חסומה ויש לה מספר סופי של נקודות אי רציפות, אז היא אינטגרבילית.
• אם $f$ אינטגרבילית ב $[a,b]$ ו $g$ היא פונקצייה המתקבלת מ $f$ על ידי שינוי ערכיה במספר סופי של מקומות כלומר $g(x)=f(x)$ חוץ ממספר סופי של $x$ בקטע. אז יתקיים ש ${\int }_a^{b}f={\int }_a^{b}g$ . (זה טענה די זהה לטענה שמעל).

משפטי תחשיב על אינטגרלים

• אם $f$ אינטגרבילית ב $[a,b]$ אז היא אינטגרבילית בכל תת קטע שלו.
• אם $f$ אינטגרבילית ב $[a,b]$ ו $c\in (a,b)$ אז

• יהי $f,g$ מוגדרות ב $[a,b]$ אם הן אינטגרביליות שם , מתקיים

היו $f,g$ אינטגרביליות על $[a,b]$. אז $f\cdot g$ אינטגרבילית ב $[a,b]$ . ואם קיים $c>0$
כך ש ${\mathrm{\forall }}_{x\in [a,b]}:|f(x)|>c$ אזי $\frac{1}{f}$ אינטגרבילית ב $[a,b]$. (זה לא הרכבה אלא לכל $x$ מכפילים את הערכים ומקבלים פונקצייה חדשה שהיא כפל הערכים הללו) .

• תהי $f$ אינטגרבילית ב$[a,b]$ עם ערכים בקטע $[c,d]$ ותהי $g$ פונקצייה הרציפה שם. אז $g\circ f$ אינטגרבילית ב$[a,b]$.

• יהיו $f,g$ אינטגרביליות ב $[a,b]$ . אם $f(x)\le g(x)$ בכל הקטע , אז ${\int }_a^{b}f\le {\int }_a^{b}g$ . ובפרט אם ניקח את החסם העליון והתחתון של הפונקצייה $m\le f\le M$ , אזי $m(b-a)\le {\int }_a^{b}f\le M(b-a)$ . וגם אם $f\ge 0$ אז ${\int }_b^{a}f\ge 0$ .

• אי שיוויון המשולש- תהי $f$ אינטגרבילית ב $[a,b]$ . אז $|f|$ אינטגרבילית ב$[a,b]$ ויתקיים

נשים לב שההפך לא נכון ניתן להפריך עם פונקציית דריכלה.

המשפט היסודי

לפי ההגדרות שנתנו לאינטגרל, נראה שהוא יצור שונה לגמרי מהנגזרת ואין שום קשר בינהם. עם זאת, לא כך המצב. כדי לדבר על המשפט היסודי נרצה להרחיב את ההגדרות שלנו לסימון האינטגרל. עד כה סימנו אינטגרל כ ${\int }_a^b$ כאשר $b>a$ . נרצה לכליל את ההגדרה גם עבור המצב ההפוך.

הגדרה אם $b>a$ ו $f$ אינטגרבילית בקטע $[a,b]$ . אז יתקיים

כמו כן, הליניאריות שהראנו למעלה מתקיימת בלי קשר לסדר היחסי בינם .

המשפט היסודי :

• אם $f$ רציפה בקטע $[a,b]$ אזי $F(x)=\underset{a}{\overset{x}{\int }}f(t)dt$ (פונקציית השטח) רציפה וגזירה ב $[a,b]$ ומתקיים

בנוסף, היא גזירה חד צדדית בקצוות ומקיימת

כלומר בנקודות בהן $f$ רציפה, פונקציית השטח שלה היא הפונקצייה הקדומה.

מסקנה מתבקשת מזה היא שאם $F(x)=G(x)$ פונקציות שטח שוות אזי $f(x)=g(x)$.

• נוסחת ניוטון לייבניץ. כדי להגדיר את הנוסחה נרצה לדבר על פונקצייה קדומה . תהי פונקצייה $f$ המוגדרת ב$D$ . $F$ נקראת קדומה של $f$ אם, $F$ גזירה ב $D$ ובכל נקודה $x\in D$ מתקיים $F^{\prime }(x)=f(x)$ . המסקנה מהמשפט היסודי ומהגדרה זו היא שלכל פונקצייה רציפה בקטע יש פונקצייה קדומה.

כעת, נוכל לדבר על הנוסחה: אם $f$ רציפה ב $[a,b]$ ו $F$ הפונקצייה הקדומה של $f$ בקטע זה, אז:

ממשפט זה וממשפט לגראנז׳ נובע משפט ערך הביניים האינטגרלי שאומר:
אם $f$ פונקצייה רציפה בקטע $[a,b]$. אז קיימת נקודה $c\in [a,b]$ כך ש

יישומים של החלק הראשון של המשפט היסודי

הוכחה :
לפי נוסחת ניוטון לייבניץ יתקיים

כעת נקבל לפי החלק הראשון של המשפט היסודי וכללי גזירה בסיסיים (בפרט כלל השרשרת) נקבל את הנ״ל.

נוסחה לחישוב אורך גרף פונקצייה

אורך הגרף של $f$ בקטע $[a,b]$ מוגדר להיות

האינטגרל הלא מסויים

בעעית אינטגרצייה לא מסויימת היא בעצם תת בעיה של מציאת האינטגרל המסויים. בעיה זאת מבקשת מאיתנו למצוא את הפונקצייה הקדומה. בעצם זאת הבעיה ההפוכה מגזירה, אך היא קשה יותר מפעולת הגזירה ולא תמיד ניתנת לביצוע. אחת הסיבות שמקשות על מציאת פונקצייה קדומה היא העובדה שיכולה להיות לנו פונקצייה אלמנטרית שהקדומה שלה לא אלמנטרית למשל הפונקצייה $e^{x^2}$ .

הגדרה תהי $f$ פונקצייה אינטגרבילית בתחום כלשהו. קבוצת הפונקציות הקדומות נקראת האינטגרל הלא מסויים של $f$ ומסומנת $\int f$ .

נשים לב שבכוונה אמרנו קבוצה הסיבה לכך היא שכל שתי פונקציות קדומות $F,G$ של אותה פונקצייה $f$ בקטע $I$ שבה היא מוגדרת, מובדלות אחת מהשנייה בקבוע חיבורי נסמנו $C$. כשנפתור את האינטגרל הלא מסויים, תמיד צריך להוסיף את הקבוע החיבורי הזה. בחישוב האינטגרל המסויים האפשר להתעלם ממנו (פשוט נתייחס ל $C=0$).
כאשר תחום ההגדרה של $f$ אינו קטע, המצב מעט שונה.

למשל: התחום של הפונקצייה $f(x)=-\frac{1}{x^2}$ הוא $\mathbb{R}/\{0\}$ והפונקצייה $F(x)=\frac{1}{x}$ היא הפונקצייה הקדומה. אבל גם

היא הקדומה שלה, ואינה נבדלת מ $F$ בקבוע.

אינטגרלים מידיים

• אם $a\ne 1$

• $$\int \frac{1}{x}dx=ln|x|+C$$
• $$\int \cos (x)dx=\sin (x)+C$$
• $$\int \sin (x)dx=-\cos (x)+C$$
• $$\int \frac{1}{x^2+1}=\arctan (x)+C$$
• $$\int \frac{1}{\sqrt{1-x^2}}dx=\arcsin (x)+C$$
• $$\int e^{x}dx=e^x+C$$
• $$\int a^{x}dx=\frac{a^x}{\ln (a)}+C$$

אציין, שחשוב להכיר זהויות טריגונומטריות בישביל לפתור אינטגרלים עם פונקציות טריגונומטריות בתוכן.

ליניאריות האינטגרל

• לכל זוג פונקציות $f,g$ בעלות תחום משותף מתקיים

• לכל קבוע $c$ מתקיים

מסקנה , לכל $n\in \mathbb{N}$ , אנו מקבלים נוסחה כללית לפונקצייה הקדומה של פולינום:

ומכאן שקדומה של פולינום היא גם כן פולינום.

אינטגרציה בחלקים

אינטגרצייה בחלקים היא המקבילה לכלל הכפל בנגזרות.

אם $f,g$ הן פונקציות בגזירות ברציפות (כלומר שהנגזרת שלהן רציפה) אז מתקיים

אינטגרצייה בחלקים ממירה את בעיית החישוב של $\int f^{\prime }g$ בבעיית החישוב של $\int f{g}^{\prime }$ . על מנת להשתמש בשיטה זו עלינו לזהות צורה של מכפלה כזו. ונשים לב שבכללי כדאי להשתמש בשיטה הזאת אם בעיית החישוב השנייה קלה יותר, וזה יקרה כאשר הגורם השני נהיה פשוט יותר לאחר גזירה.

טכניקות עזר

• לעתים כשהאינטגרנד אינו נראה כמו מכפלה, אפשר בכל זאת לרשום אותו כמכפלה של עצמו עם $1$.
• כאשר יש פולינום כפול פונקצייה אחרת באינטגרנד אפשר לגזור את הפולינום כדי להקטין את מעלתו.
• אם יש מעלה גבוהה בפולינום, נצטרך לעשות אנטגרצייה בחלקים כמה פעמים.
• לעתים, לאחר ביצוע אינטגרצייה בחלקים כמה פעמים , אנו מקבלים את אותו הביטוי שהתחלתנו איתו, נוכל לנצל את זה כדי להעביר אגפים ולחלץ את האינטגרל שהתחלנו ממנו ולקבל באגף ימין את התוצאה הרצוייה.

שיטת ההצבה

שתי שיטות האינטגרצייה שנדבר עליהן הן גרסאות של כלל השרשרת לנגזרת.

הצבה ישירה

נניח ש $F^{\prime }=f$ בקטע $I$. ותהי פונקצייה גזירה $g$ מקטע כלשהו $J$ לקטע $I$ כך ש $F\circ g$ וגם $f\circ g$ מוגדרות בקטע $J$ .
אזי:

המסקנה המתבקשת מכך היא

שיטת ההצבה מאפשרת להפוך את האינטגרנד לפשוט יותר , על ידי המרת בעיית האינטגרצייה $\int f(g(x))g^{\prime }(x)dx$ לבעיה של $\int f(y)dy$ .

שיטת ההצבה מכונה גם החלפת משתנה. בשפה זו, מתארים את המעבר שדיברנו עליו, כאילו המשתנה $g(x)$ הוחלף במשתנה $y$. כשמבצעים החלפה כזאת חשוב לשים לב להחליף את $g^{\prime }(x)dx$ ב $dy$ . כלומר

דוגמאות

האינטגרנד הוא מהצורה $g^2(x)g^{\prime }(x)$ עבור $g(x)=\sin (x)$ . ולכן הוא מהצורה $f(g(x))g^{\prime }(x)$ כאשר $f(t)=t^2$ . ולכן נקבל

האינטגרנד הוא מהצורה $f(g(x))g^{\prime }(x)$ כאשר
$g(x)=x^2$ , $f(t)=e^t$ . כלומר נסמן $x^2=t$ ויתקיים

הצבה הפוכה

נניח ש $f$ מוגדרת בקטע כלשהו $I$ , ותהי $g$ פונקצייה גזירה מקטע כלשהו $J$ לקטע $I$, כך שהפונקצייה $f\circ g$ מוגדרת בקטע $J$ . נניח בנוסף כי $g$ הפיכה. אם $F$ תקיים

אז

המסקנה המתבקשת היא

נשים לב בניגוד להצבה הישירה שבה אנחנו מחליפים את הפונקצייה התלויה ב $x$ בנעלם, כאן אנחנו מחליפים את הנעלם בפונקצייה $g(x)$ . כלומר, אנחנו עוברים מבעיית האינטגרצייה $\int f(x)dx$ לבעיה $\int f(g(t))g^{\prime }(t)dt$ . הכלל הוא שכאן יש להחליף את $dx$ ב $g^{\prime }(t)dt$ . כלומר

דוגמאות

1. $$\int \frac{\sqrt{x}}{x^{\frac{3}{2}}+1}dx$$

נרצה להפטר מהשורשים, כלומר נחליף את $x=t^2$ ונסמן $g(t)=t^2$ וכעת

כעת נציב את הפונקצייה ההופכית ל $g$ שהיא $\sqrt{x}$ ונקבל

2. $$\int \sqrt{1-x^2}dx$$

נשים לב לזהות הטירגונומטרית הבאה $\sqrt{1-{\sin }^2(x)}=\cos (x)$ . נוכל לסמן $x=g(t)=sin(t)$ ונקבל

כעת נשאר להציב את ההופכית של $g(t)$ במקום $t$ ונקבל

לסיכום

• ההצבה הישירה תקרה כאשר נשים לב למבנה של פונקצייה פנימית כפול הנגזרת שלה, נציב $t$ כפונקצייה הפנימית.
• ההצבה ההפוכה קצת יותר מורכבת, ובה נשתמש כדי להגיע למצב שבוא יש לנו מבנה שמזכיר את המבנה הראשון שדיברנו עליו. נעשה זאת על ידי כך שנזהה שנוכל להציב פונקצייה במקום הנעלם באופן כזה שיוביל אותנו למבנה מהצורה הראשונה.

פונקציות רציונליות

באופן כללי, אין הבטחה שאינטגרל של פונקצייה אלמנטרית תיתן פונקציה קדומה אלמנטרית. יוצאת מן הכלל הזה, היא משפחת הפונקציות הרציונליות. לפונקצייה כזאת תמיד יש פונקציה קדומה אלמנטרית, ויתר על כך יש שיטה לחשב אותה.

הגדרה פולינום $p$ נקרא אי פריק, אם לכל שני פולינום $r,s$ המקיימים
$p=r\cdot s$ , אחד הפולינומים הוא ממעלה 1.

אפשר להוכיח באינדוקצייה על המעלה ש כל פולינום ניתן לכתיבה כמכפלה של פולינומים אי פריקים.

משפט כל פולינום אי פריק הוא ממעלה $1$ או $2$.
נובע מכאן שכל פולינום הוא מכפלה של פולינומים ממעלה אחת ושתיים, כי הוא שווה למכפלה של פולינומים אי פריקים.
פולינום ריבועי אי פריק הוא פולינום ללא שורשים לפי משפט הפירוק הריבועי מהתיכון.

משפט תהי $\frac{p}{q}$ פונקצייה רציונלית. אז אפשר לרשום אותה כסכום

כאשר $r,s_i,t_i$ פולינומים ו $k_i$ מספרים טבעיים המקיימים :

• $\mathrm{deg}r<\mathrm{deg}p-\mathrm{deg}q$ ואם $\mathrm{deg}p<\mathrm{deg}q$ אז $r=0$
• $t_i$ גורם אי פריק של $q$ ו $(t_i{)}^{k_i}$ גורם של $q$ .
• $\mathrm{deg}{s}_i<\mathrm{deg}{t}_i$ כלומר $\mathrm{deg}{s}_i\le 1$ ואם $\mathrm{deg}{t}_i=1$ אז $s_i$ קבועה.

נשים לב שהפירוק מכריח אותנו ש $q$ יהיה פולינום פריק.

דוגמאות

• $$f(x)=\frac{1}{x^2-1}$$

אנחנו יודעים שאפשר לרשום את המכנה בתור מכפלה $x^2-1=(x+1)(x-1)$ ולכן מהמשפט אנחנו יודעים שניתן לבטא את $f$ בצורה הבאה

כאשר $A,B$ הם קבועים (נשים לב גם ש $r$ הוא 0 בגלל שהדרגה של המונה גדולה מהמכנה).

השלב הבא הוא שנעשה מכנה משותף ונקבל

ולכן נשאר להשוות בין המונים ששניהם פולינום, לפי שיוויון פולינומים אנחנו יודעים שחייבים שיהיו להם את אותם המקדמים ולכן

המקדם של $x$ שווה ל0 ו $A=B+1$ כלומר סך הכל נקבל מהפתרון ש $A=\frac{1}{2}$ ו $B=\frac{-1}{2}$
סך הכל נקבל

2. $$f(x)=\frac{x^4-2x^3-x^2-5}{(x^2+x+1)(x-3)}$$

נשים לב שהפולינום הריבועי במכנה הוא אי פריק, לכן יש לנו שני גורמים אי פריקים במכנה, לכן נוכל לרשום את הפונקצייה הרציונלית הנ״ל באופן הבא

סך הכל שוב פעם נוכל לעשות מכנה משותף ונקבל

לסיכום:

• השלב הראשון יהיה לפרק את המכנה לכפל של גורמים אי פריקים או כפל של גורמים אי פריקים שאחד מהם בחזקה כלשהי.
• נבין מה ההפרש במעלה בין המכנה למונה ככה נדע האם $r$ הוא פולינום שאינו פולינום ה $0$.
• נבצע פירוק לפי המשפט.

דגשים

1. לפעמים הדרגה במונה תהיה יותר גדולה מהמכנה בהפרש הגדול מ $2$. זה יכול להיות בעייתי כיוון שכעת ל $r$ יכולות להיות מספר אפשרויות. במצב כזה נבצע חילוק פולינומים כדי לדעת כמה פעמים הפולינום במכנה מוכל בפולינום במונה, ואם ישנה שארית אז היא תהיה בהכרח פונקצייה רציונלית כשהדרגה במכנה גדולה יותר ואז נוכל לעשות את האלגוריתם שאנחנו מכירים.

נחלק פולינום לדוגמה :

האלגוריתם ילך באופן הבא:

• עבור הגורם עם המעלה הכי גבוהה במחלק , נבין במה צריך להכפיל אותו כדי להגיע למחולק עם המעלה הכי גבוהה.
• אחרי שהבנו מהו הגורם שבו צריך להכפיל, נכפיל אותו בכל המחלק ונחסיר מהמחולק את התוצאה הזאת. נקבל פולינום חדש.
• נתייחס לפולינום החדש במחלק ונמשיך את התהליך הזה באופן ריקורסיבי עד שהמעלה שפולינום החדש נמוכה יותר מהמעלה של המחלק.
• הפולינום שנקבל בסוף התהליך הריקורסיבי הוא השארית (אם נקבל 0 אין שארית). והגורמים שהכפלנו לאורך התהליך הם גורמים ליניאריים שיש לחבר אותם אחד עם השני ועם השארית סך הכל (את השארית כמובן צריך לחלק במכנה המקורי, כי זאת השארית שלו, בדומה לשארית).
• נרשום את התוצאה הסופית כחיבור של הגורמים שהכפלנו עם השארית

במקרה שלנו השלב הראשון הוא להכפיל את המחלק ב $x$ כדי זה מה שצריך להכפיל כדי ש $x^2$ יהיה יהיה הגורם עם המעלה הכי גבוהה במחולק, במקרה שלנו $x^3$
נכפיל את כל המחלק ב $x^{}$ ונחסר מהמחולק נקבל

כעת נמשיך את התהליך באופן ריקורסיבי, נכפיל את $x^2$ ב $3$ כי אז הגורם עם המעלה הכי גבוהה במחלק יהיה שווה לגורם עם המעלה הכי גבוהה בפולינום החדש. נחסר ונקבל

כאן אפשר לעצור, זאת השארית שלנו. סה״כ נקבל

וכמו שאמרתי , נוכל כעת לבצע פירוק לשברים חלקיים בצורה נוחה יותר על הפונקצייה הרציונלית שנשארה לנו.

נשים לב שזה לא משנה כמה גורמים יש במחולק, מה שחשוב זה להכפיל כדי להגיע לגורם עם הדרגה הכי גבוהה בו כל פעם .

2. לפי הנוסחה שנתנו, יכול להיות מצב ש $q(x)$ מורכב מגורמים אי פריקים שאחד מהם בחזקה מסויימת, במצב זה נשים לב (כמו שרשום בנוסחה אך זה יכול מעט לבלבל ולכן מסביר פה), שבחיבור של הפונקציות הרציונליות , עבור הגורם האי פריק בחזקה , אנחנו נסכום אותו באופן כזה שכל פעם עולים בחזקה שלו במכנה ובמונה נשאר אותו הגורם . זה ניסוח קצת מבלבל אז אסביר זאת בדוגמה

הסכום של הגורמים (בהינתן והדרגה של המונה קטנה יותר) מורכב מכל החזקות האפשריות של הגורם האי פריק (אם זה היה 3 אז היינו מוסיפים חיבור של גורם נוסף).
זה בהנחה שהגורם בתוך החזקה הוא אי פריק, אם הוא לא צריך לפרק אותו .

איך זה בא לידי ביטוי באינטגרלים?

עכשיו כשאנחנו יודעים כיצד לפרק פונקציות רציונליות, נוכל להשתמש בליניאריות האינטגרל כדי לחשב את כל אחד מסוגי המחוברים המופיעים בפירוק, ואנחנו יודעים בידיוק איך הצורות של כל מחובר יכולה להראות (אם מתעלמים מכפל בקבוע):

1. פולינום
2. פונקצייה מהצורה $\frac{1}{(x+a{)}^k}$ .
3. פונקצייה מהצורה $\frac{1}{(x^2+ax+b{)}^k}$ . כאשר המכנה בתוך החזקה אי פריק.
4. פונקצייה מהצורה $\frac{x+c}{(x^2+ax+b{)}^k}$ . כאשר המכנה בתוך החזקה אי פריק.

נראה כעת איך לחשב את כל אחד מהאפשרויות:

1. אנחנו יודעים בקלות לחשב אינטגרל של פולינום.

3. נרצה להביא את האינטגרל מהצורה הזאת, לאינטגרל מהצורה $\int \frac{c}{y^2+1}dy$ .
   נשים לב ש

נשים לב ש $b-\frac{a^2}{4}$ הוא ביטוי חיובי תמיד (זה עובד בגלל שהפולינום אי פריק). נוכל להציב $c=\sqrt{b-\frac{a^2}{4}}$ ונקבל :

כאשר ביצענו הצבה ישירה $y=\frac{x}{c}+\frac{a}{c}$ ולכן גם $dy=y^{\prime }dx$ כלומר $dx=\frac{dy}{y^{\prime }}$ .

מכאן יש שני אפשרויות :

• אם $k=1$ אז זה אינטגרל של $arctan(y)$ .
• אחרת נוכל לבנות ביטוי ריקורסיבי אך לא נתעסק בזה...

4. $$\begin{array}{c}\int \frac{x+c}{(x^2+ax+b{)}^k}=\frac{1}{2}\int \frac{2x+a}{(x^2+ax+b{)}^k}\end{array}+(c-\frac{a}{2})\int \frac{1}{(x^2+ax+b{)}^k}$$

ואת שני האינטגרלים הנ״ל אנחנו יודעים לפתור (הביטוי הראשון זה פונקצייה והנגזרת שלה, והשני זה בידיוק ביטוי 3).

פונקציות רציונליות

כאשר האינטגרנד מכיל סכומים, מכפלות ומנות של פונקציות טריגונומטריות , אפשר להמיר את בעיית האינטגרצייה בבעיית אינטגרציה של פונקציות רציונליות.
השיטה מבוססת על הצבת ווירשטראס : $t=\tan (\frac{x}{2})$ ועל הזהויות הבאות:

אינטגרלים לא אמיתיים

בגדול ישנם שני סוגים של אינטגרליים לא אמיתיים:

אינטגרליים לא אמיתיים בקטע אינסופי

הגדרה : תהי $f:[a,\mathrm{\infty })\to \mathbb{R}$ - פונקצייה אינטגרבילית בכלל תת קטע סגור $[b,c]\subseteq [a,\mathrm{\infty })$ . אם קיים הגבול

אז הוא נקרא אינטגרל לא אמיתי של $f$ בתחום ומסומן ${\int }_{[a,\mathrm{\infty })}f$ . נאמר שהאינטגרל הזה מתכנס וש$f$ אינטגרבילית.

בעצם אנחנו מכלילים את מושג האינטגרל שדיברנו עליו למקרים שבהם הפונקצייה מתכנס באינסוף למשל:

הגדרות נוספות לאינטגרלים לא אמיתיים בקטע אינסופי

כאשר במקרה השלישי חייב ששני האינטגרלים בצד שמאל יתקיימי כדי שהאינטגרל בצד ימין יהיה קיים (בשונה מגבולות של סדרות שאנחנו יודעים שגם במקרה ששני הגבולות לא קיימים עדיין ייתכן שהגבול יהיה קיים, הסיבה שפה זה לא עובד כי אנחנו יודעים שאין חפיפה בין שני האינטגרלים האלו, כלומר כל אחד מהם מתייחס ל״אזור״ אחר בפונקצייה, בהסבר אינטואיטיבי ולא מתמטי).

כעת נשים לב , בפונקציות פשוטות נוכל פשוט לחשב את האינטגרל לפי המשפט היסודי ולאחר מכן לחשב את הגבול וכך נדע אם יש התכנסות או התבדרות יחסית מהר.

ברוב המקרים, האינטגרלים יהיו מורכבים בכדי לקבוע התכנסות או התבדרות עם הכלים שאנחנו מכירים מחישובי גבולות ולכן נרצה להשתמש במבחני השוואה על מנת לקבוע התכנסות או התבדרות .

משפט תהי $f:[a,\mathrm{\infty })\to \mathbb{R}$ פונקציה. אם $\underset{x\to \mathrm{\infty }}{lim}f(x)=L\ne 0$ אז $f$ אינה אינטגרבילית במובן הרחב ב $[a,\mathrm{\infty })$ .

מבחן ההשוואה הראשון

תהי $f,g:[a,\mathrm{\infty })\to \mathbb{R}$ פונקציות אי שליליות אינטגרביליות בכל תת קטע סגור.
יתקיים ש אם $f\le g$ :
אם - ${\int }_a^{\mathrm{\infty }}g$ מתכנס אז ${\int }_a^{\mathrm{\infty }}f$ מתכנס (וכמובן יש גם את טענה ה cp).

מבחן ההשוואה השני

תהי $f,g:[a,\mathrm{\infty })\to \mathbb{R}$ פונקציות אי שליליות אינטגרביליות בכל תת קטע סגור.
אם קיים הגבול $\underset{x\to \mathrm{\infty }}{lim}\frac{f(x)}{g(x)}=L$ אז:

1. אם $L\in (0,\mathrm{\infty })$ , האינטגרלים ״חברים״ כלומר שאם האחד מתכנס כך גם השני.
2. אם $L=0$ אז אם - ${\int }_a^{\mathrm{\infty }}g$ מתכנס אז ${\int }_a^{\mathrm{\infty }}f$ מתכנס (וכמובן יש גם את טענה ה cp).
3. אם $L=\mathrm{\infty }$ אז אם - ${\int }_a^{\mathrm{\infty }}f$ מתכנס אז ${\int }_a^{\mathrm{\infty }}g$ מתכנס (וכמובן יש גם את טענה ה cp).

נשים לב, אם הפונקצייה שלילית, אז המבחנים גם עובדים, רק צריך להוציא סקלר $-1$ .

מבחן דריכלה

(שימושי בעיקר ב ״פונקציות מזגזגות בין מספרים חיוביים לשליליים״)
נוכל להסיק ש ${\int }_a^{\mathrm{\infty }}f(x)g(x)dx$ מתכנס אם :

1. $f$ מונוטונית , יורדת ל 0
2. $g$ מקיימת שפונקציית השטח שלה ${\int }_a^{x}g(t)dt$ חסומה (עושים זאת לפי המשפט היסודי ואז מראים שכ $x\to \mathrm{\infty }$ עדיין השטח חסום בערך מסויים.)

התכנסות בהחלט

הגדרה פונקצייה $f:[a,\mathrm{\infty })\to \mathbb{R}$ נקראת אינטגרבילית בהחלט בקטע אם $|f|$ אינטגרבילית שם. במקרה זה נאמר ש ${\int }_a^{\mathrm{\infty }}f$ מתכנס בהחלט.

משפט אם ${\int }_a^{\mathrm{\infty }}f$ מתכנס בהחלט, אז הוא גם מתכנס. כלומר אם $f$ אינטגרבילית בהחלט בקטע אז היא גם אינטגרבילית בו.

אינטגרליים לא אמיתיים כאשר הפונקצייה לא חסומה בנקודה

באופן דומה לסוג הראשון, אנחנו מכלילים את מושג האינטגרל למצבים בהם יש אסימפטוטות בנקודות מסויימות בגרף, יכול להיות מצבים שיש אסימפטוטה אך עדיין האינטגרל מתכנס.

הגדרה אם יש אסימפטוטה ב $a$ אז

ובאופן דומה אם יש אסימפטוטה ב $b$ אז

למעשה, אין חובה בהגדרה הזאת שתהיה אסימפטוטה בנקודה, מדובר בהכלל של האינטגרל החסום בקטע סגור על מקרה של קטעים חצי סגורים. כמובן גם שהשיווין מתקיים בהינתן שקיים גבול בכלל. אם קיים כזה (במובן הצר) אז $f$ נקראת אינטגרבילית בקטע החצי סגור. אחרת היא אינה אינטגרבילית בו. הגבול הנ״ל נקרא, אינטגרל לא אמיתי.

דגש לפתרון בעיות במידה ואנחנו רוצים לבדוק אינטגרביליות בקטע פתוח לגמרי אז נפצל לשתי קטעים או יותר חצי פתוחים וסגורים. כמו כן, במידה ויש נקודה בעייתית בתוך הקטע, גם כן נפצל באותו אופן. (באותו אופן להסבר למעלה, צריך שכולם יתכנסו בנפרד כדי שתהיה התכנסות כוללת, אחרת מספיק שאחד מתבדר כדי שכל האינטגרל יתבדר).

נשים לב שאם פונקצייה אינטגרבילית בקטעים כאלה אז התכונות של פונקציות אינטגרביליות שדיברנו עליהם בפרק של אינטגרלים מסויימים מתקיימות בכל הקטע .

מבחני השוואה: מבחני ההשוואה זהים למבחני ההשוואה שדיברנו עליהם מקודם , הדרישה הפעם היא ששתי הפונקציות מוגדרות באותו קטע עם אותה נקודה בעייתית באחת הקצוות. וכמובן שצריך ש $x$ ישאף לנקודה הבעייתית הזו. (דריכלה רלוונטי רק לסוג 1).

אינטגרלי $p$

יש איזשהו מבנה של אינטגרל לא אמיתי מוכר ${\int }_a^{\mathrm{\infty }}\frac{1}{x^p}dx$ הנקרא אינטגרל $p$ .
במקרה הנ״ל האינטרל יתכנס אם ורק אם $p>1$ (כמו בטורים).

אפשר להגדיר אינטגרל $p$ גם על הסוג השני והוא ייראה מהצורה ${\int }_a^b\frac{1}{(x-a{)}^p}dx$ וזה יתכנס אם ורק אם $p<1$ .

טיפ :

• מומלץ להמליץ לאינטגרלים לא אמיתיים שהאינטגרנד שלהם לא חיובי $t=\frac{1}{x-a}$ עבור $a$ נקודה בעייתית, כדי להמיר את בעיית האינטגרל הלא אמיתי מסוג שני לסוג 1.

• אם יש נקודה שבה גם המונה וגם המכנה יוצא $0$ , צריך לבדוק (מומלץ עם כללי לופיטל) אם זאת אכן, נקודה בעייתית.