Reverse Polish Notation

Reverse Polish notation (RPN) is a method for representing expressions in which the operator symbol is placed after the arguments being operated on. Polish notation, in which the operator comes before the operands, was invented in the 1920s by the Polish mathematician Jan Lucasiewicz. In the late 1950s, Australian philosopher and computer scientist Charles L. Hamblin suggested placing the operator after the operands and hence created reverse polish notation.

Reverse Polish notation, also known as postfix notation, contrasts with the "infix notation" of standard arithmetic expressions in which the operator symbol appears between the operands.

RPN has the property that brackets are not required to represent the order of evaluation or grouping of the terms. RPN expressions are simply evaluated from left to right and this greatly simplifies the computation of the expression within computer programs.

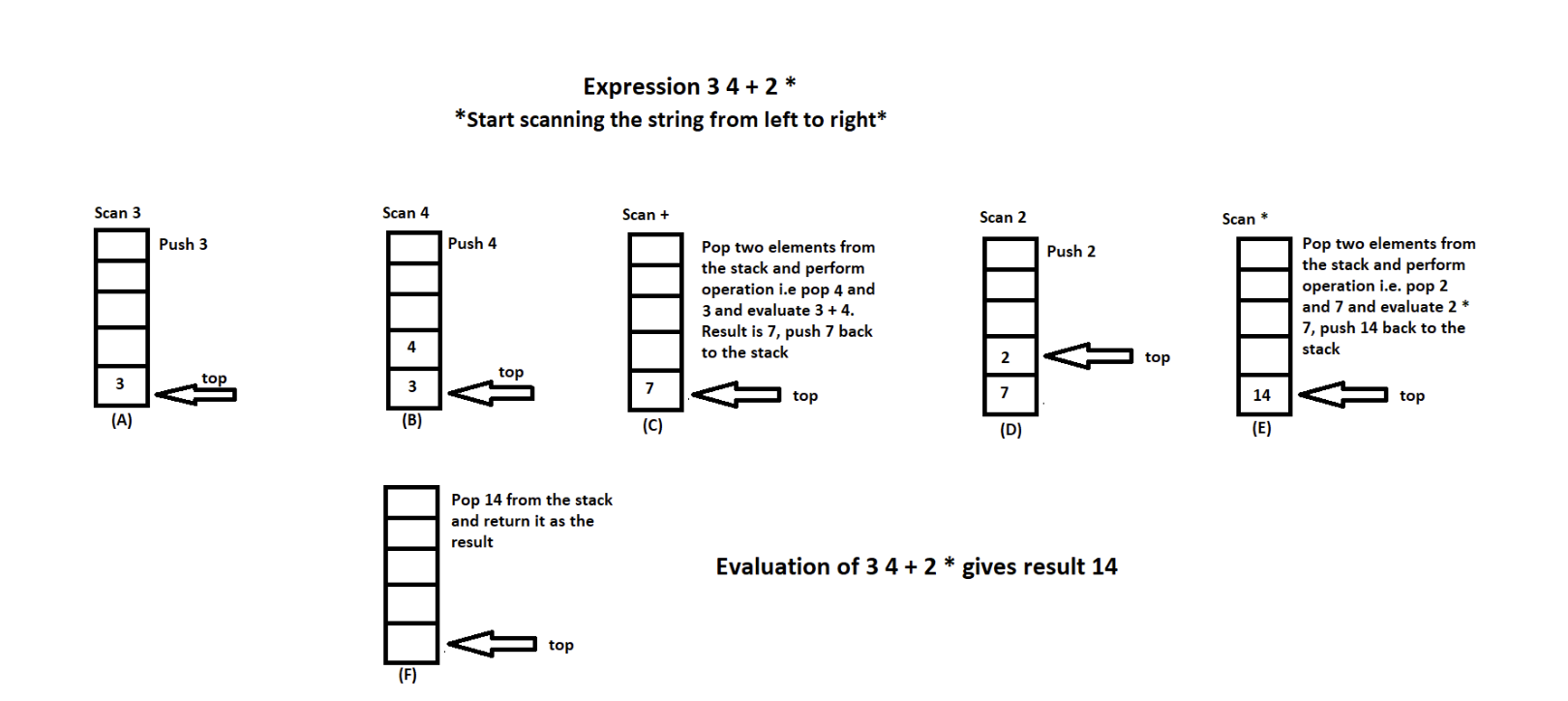
As an example, the arithmetic expression $(3+4)\times 5$ can be expressed in RPN as $34+5\times$

In practice RPN can be conveniently evaluated using a stack structure. Reading the expression from left to right, the following operations are performed:

1. If a value appears next in the expression, push this value on to the stack.

2. If an operator appears next, pop two items from the top of the stack and push the result of the operation on to the stack.

class EvalReversePolishNotation {
    public static int evalRPN(String s) {
 
        // stack to store operands
        java.util.Stack stack = new java.util.Stack<Integer>();
        String tokens[] = s.split(" ");
        int expLength = tokens.length;
 
        // parse the entire expression
        for (int i = 0; i < expLength; i++) {
            int result, element1, element2;
            switch (tokens[i]) {
            case "+":
                element1 = (Integer) stack.pop();
                element2 = (Integer) stack.pop();
                result = element2 + element1;
                stack.push(result);
                break;
            case "-":
                element1 = (Integer) stack.pop();
                element2 = (Integer) stack.pop();
                result = element2 - element1;
                stack.push(result);
                break;
            case "*":
                element1 = (Integer) stack.pop();
                element2 = (Integer) stack.pop();
                result = element2 * element1;
                stack.push(result);
                break;
            case "/":
                element1 = (Integer) stack.pop();
                element2 = (Integer) stack.pop();
                result = element2 / element1;
                stack.push(result);
                break;
            default:
                result = Integer.parseInt(tokens[i]);
                stack.push(result);
 
            }
        }
        return (Integer) stack.pop();
    }
 
    public static void main(String[] args) {
        int result = evalRPN("4 13 5 / +");
        System.out.println("Result of evaluation = " + result);
        int result1 = evalRPN("10 6 9 3 + -11 * / * 17 + 5 +");
        System.out.println("Result of evaluation = " + result1);
    }
}

Time and space complexity

Considering n = length of input Reverse Polish Expression, $d$ = number of operands/digits, $o$ = number of operators, the time complexity of the above implementation is $O(n)$, since we are scanning the entire string. Time taken by push and pop operations is constant i.e. $O(1)$ constant time complexity.

Space complexity = $O(d)$, since we store only operands/digits in the stack and this is the worst case for space complexity in which we push all the operands to the stack, e.g. $234\ast +$.