#algorithms #computer_science

אלגוריתמים הסתברותיים

אלגוריתם הסתברותי הוא אלגוריתם שמקבל מחרוזת אקראית $r$ כקלט.
ישנם מספר דרכים למדל את $r$ אבל למטרה שלנו נניח ש $r$ מכיל מספרים אקראיים בין $0$ ל $n$ כאשר $n$ הוא גודל הקלט של האלגוריתם. כלומר יש איזשהו אלמנט אקראי שמשפיע על פלט האלגוריתם.

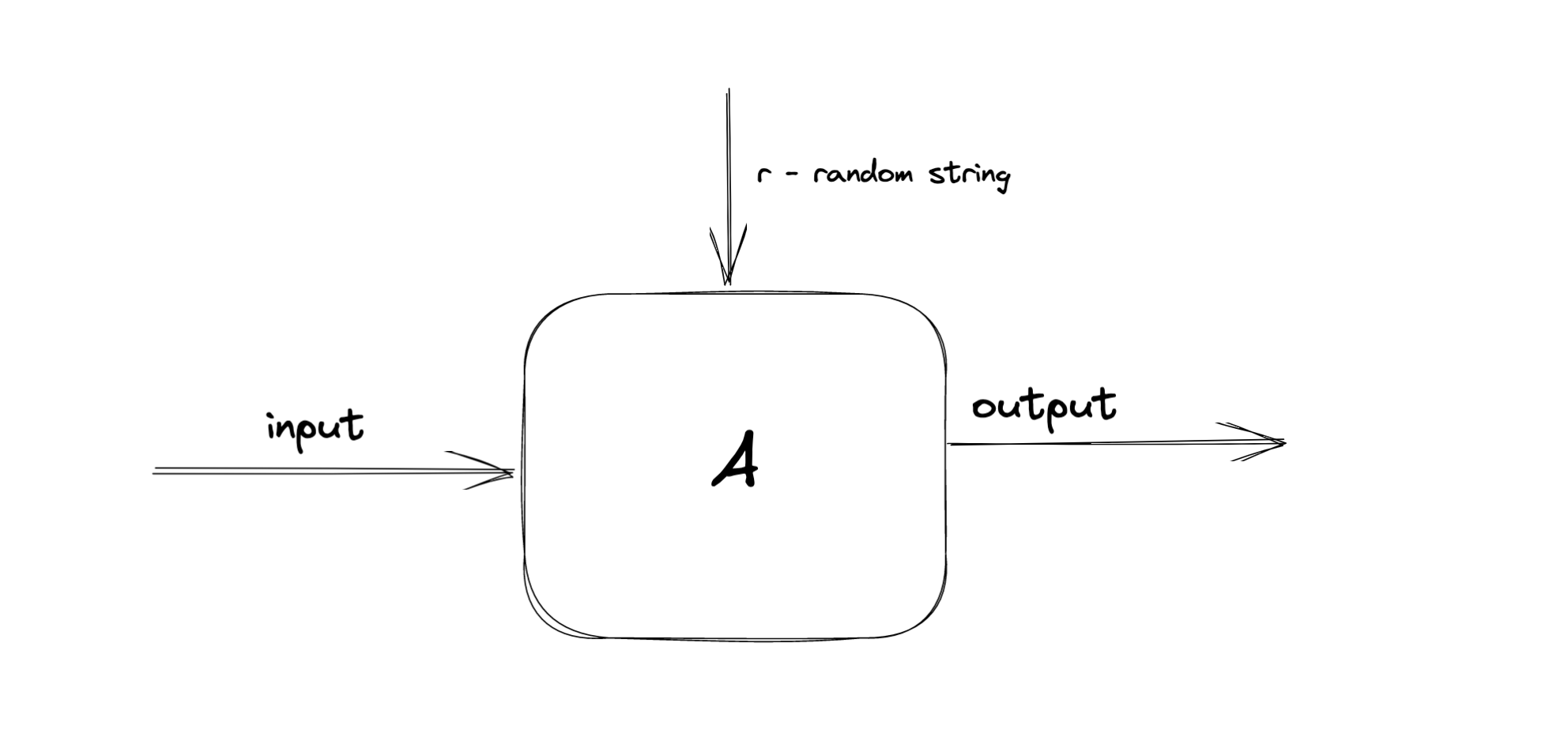
Pasted image 20230207151136.png|350

בדרך כלל, כאשר אנחנו מריצים אלגוריתם דטרמיניסטי שלא משתמש בכלים אקראיים, זמן הריצה והנכונות ברורים לנו – אנו יודעים להוכיח אותם.

ברגע שאנחנו משתמשים באקראיות ובמחרוזת $r$ , ישנם שני דברים שיכולים לקרות. של ריצה של האלגוריתם שלנו למעשה יכול

לרוץ בזמן שונה
להחזיר תשובה שונה

למשל אם האלגוריתם בוחר מספר אקראי $x$ וסופר עד $x$ , לכל מספר נקבל זמן ריצה שונה.
מקרה אחר למשל, אם המערך הוא בגודל $n$ והאלגוריתם בוחר מספר אקראי $x$ בין $1$ ל $n$ ומחזיר את האיבר במקום ה $x$ אז נקבל פלט שונה עבור $x$ שונה.

באלגוריתמים רנדומיים ישנם שני סוגים של משתנים מקריים

זמן הריצה הוא משתנה מקרי (תלוי ב $r$ )
נכונות האלגוריתם היא גם כן משתנה מקרי (היא תלויה ב $r$ )

הדוגמה הכי קלאסית לאלגוריתם עם זמן ריצה מקרי הוא Quick Sort שבו ה pivot נקבל בצורה אקראית. אם הבחירה של הפיבוט היא רעה אנחנו יכולים להגיע לזמן ריצה של $O (n^{2})$ אבל בתוחלת נקבל שזמן הריצה הוא $O (n \log n)$ .

דוגמא לאלגוריתם שלא תמיד נכון – אלגוריתם שמקבל סדרה של מספרים ורוצה להחזיר מספר זוגי מתוך הסדרה. הוא בוחר מספר באופן אקראי, אם המספר אי-זוגי והוא מחזיר אותו, אז האלגוריתם טעה. אם בוחרים רק מספרים זוגיים, אז צודקים. כלומר, נכונות האלגוריתם תלויה בקלט האקראי של הריצה.

סוגים של אלגוריתמיים רנדומים

ישנם מספר סוגים של אלגוריתמיים מקריים שאתעמק בהם כאן.

מונטה קרלו-
זמן הריצה הוא דטרמיניסטי אבל הנכונות היא משתנה מקרי, האלגוריתם עלול להצליח או לטעות. נרצה לנתח את הסיכוי לטעות ונרצה שהסיכוי לטעות יהיה כמה שיותר קטן כלומר אם גודל הקלט הוא $n$ נרצה לטעות בסיכוי $\frac{1}{n^{α}}$ .כאשר $α \geq 1$ קבוע.

לאס וגאס-
האלגוריתם תמיד מצליח אבל זמן הריצה הוא משתנה מקרי. נרצה לנתח את התכונות ההסתברויות של זמן הריצה:

תוחלת זמן הריצה.
חסם עליון לזמן הריצה בסיכוי גבוה.

וידוא כפל מטריצות בינאריות

נציג אלגוריתם מונטה קרלו לוידוא של כפל מטריצות בינאריות. כלומר כל האריתמטיקה של המטריצות היא מעל $Z_{2}$ .

קלט: 3 מטריצות בינאריות $A, B, C$ מגודל $n \times n$
פלט: האם $C = A \cdot B$

הנאיבי הוא כמובן להכפיל עם כפל מטריצות מהיר בזמן ריצה $O (n^{ω})$ ולהשוות. אבל זמן ריצה זה לא פרקטי ונראה משהו מהיר יותר.

אם כן, נראה אלגוריתם שזמן הריצה שלו הוא $O (n^{2})$ אבל הוא טועה בסבירות יחסית גבוהה של לכל היותר $\frac{1}{2}$ .
לאחר מכן נשפר את סיכויי ההצלה לאלגוריתם שזמן הריצה שלו הוא $O (n^{2} \log n)$ אבל הוא צודק בסיכוי גבוה, כלומר הסיכוי לטעות הוא $\frac{1}{n^{α}}$ כפי שרצינו.

אלגוריתם בסיסי

verify_binary_MM_basic(A,B,C)
	choose random vector V = (v1,....,vn) of bits
	Vb = B * V
	Vab = A * Vb

	if Vab = C * V
		return true
		
	return false

נשים לב שאם $C = A B$ אזי לכל וקטור $\vec{v}$ מגודל $n$ מתקיים $C \cdot \vec{v} = A B \cdot \vec{v}$ באופן די הגיוני וזה מה שהאלגוריתם בודק.

זמן ריצה
בחירת הוקטור היא ב $O (n)$ זמן.
כל כפל עם וקטור לוקחת $O (n^{2})$
השוואה לוקחת $O (n)$ .
סה״כ $O (n^{2})$

הבחנה

אם $C = A B$ אז האלגוריתם תמיד צודק. אבל אם $C \neq A B$ אז בחירה של וקטור לא טוב יכולה לגרום לאלגוריתם לטעות (למשל וקטור ה0).

ניתוח הסיכוי לטעות
יהי $D = C - A B$ ונניח $C \neq A B$ . לכן $D \neq 0$ . בפרט זה אומר שקיים $d_{i j} = 1$ (נזכיר שהמטריצות בינאריות).

לשם הסמנטיקה נאמר שוקטור $\vec{v}$ הוא רע אם מתקיים במצב שבו $C \neq A B$ אבל

D \cdot \vec{v} = (C - A B) \vec{v} = 0

אם הוא לא רע נאמר שהוא טוב. נשים לב $\vec{v} is good \leftrightarrow D \vec{v} \neq 0$

למה
מספר הווקטורים הטובים הוא לפחות כמספר הווקטורים הרעים .

הוכחה
נתאר פונקצייה חח״ע שממפה וקטורים רעים לווקטורים טובים. יהי $\vec{v}$ וקטור רע. כלומר $D \vec{v} = 0$ אזי

\forall_{1 \leq i \leq n} : \sum_{k = 1}^{n} d_{i k} \cdot v_{k} = 0

בגלל ש $v$ רע אז מתקיים בלי הגבלת הכלליות $d_{i j} = 1$ . נגדיר

w_{j} = (\begin{matrix} 0 \\ 0 \\ ⋮ \\ 1 \\ ⋮ \\ 0 \end{matrix})

כאשר $1$ נמצא בשורה ה $j$ .

יתקיים ש

v^{'} = v + w_{j}

נראה ש $v^{'}$ וקטור טוב

\sum_{k = 1}^{n} d_{i k} \cdot v_{k}^{'} = \sum_{k = 1}^{n} d_{i k} \cdot (v_{k} + w_{k}) = \sum_{k = 1}^{n} d_{i k} \cdot v_{k} + \sum_{k = 1}^{n} d_{i k} \cdot w_{k} = d_{i j} = 1

$\sum_{k = 1}^{n} d_{i k} \cdot v_{k}$ הוא $0$ כי $v$ וקטור רע. וגם $w_{j}$ הוא האיבר היחיד שיהיה $1$ בוקטור $w_{j}$ ולכן כל האחרים יהיו $0$ .

כלומר הצלחנו לבנות פונקצייה שממפה וקטור רע לטוב.

f (v) = v + w_{j}

קל להראות שזאת פונקצייה חח״ע שכן אם הפלטים הם וקטורים טובים שווים אם נחסר מהם את $w_{j}$ המתאים לכל אחד מהם (זה לא אותו $w$ ) נקבל את הוקטור הרע ששלחנו. והם יהיו שווים.

מסקנה - הסיכוי לבחור וקטור רע הוא לכל היותר $\frac{1}{2}$ .

אמפליפיקציה

נרצה לשפר את הסיכוי לטעות. נעשה זאת באמצעות אמפליפיקציה. בשיטה זו מריצים את האלגוריתם הבסיסי $k$ פעמים.

verify_binary_MM(A,B,C)
	k = alog(n)
	for i = 1 to k
		if verify_binary_MM_basic(A,B,C) = false
			return false
	return true

חישוב הסיכוי לטעות:
על מנת שהאלגוריתם הנ״ל יטעה מספיק שנבחר פעם אחת וקטור רע כלומר שהפלט של האלגוריתם הבסיסי אמור להחזיר שהם ״לא שווים״ אבל הוא מחזיר ״שווים״ נחשב את ההסתברות לכך

\begin{matrix} P (each iteration a bad vector was chosen) \\ = P (make one iteration wrong)^{k} \leq {(\frac{1}{2})}^{k} = \frac{1}{2^{k}} \end{matrix}

המעבר הראשון נובע מאי תלות בין הבחירה של הוקטור.
כפי שאמרנו מטרתנו היא לטעות בסבירות של לכל היותר $\frac{1}{n^{α}}$ אם כן

\frac{1}{2^{k}} = \frac{1}{n^{α}} \leftrightarrow k = α \log (n)

שזה הסיבה שבחרנו את k הזה

זמן ריצה $k$ איטרציות שכל אחת $O (n^{2})$ סה״כ $O (n^{2} \log n)$ .

Quick sort פרנואידי

נסתכל על Quick Sort בהיבט יותר הסתברותי. נשים לב שזה אלגוריתם מסוג לאס וגאס שבו זמן הריצה הוא משתנה מקרי.
באלגוריתם זה אנחנו בוחרים אינדקס אקראי $r$ ומבצעים חלוקה של איברי המערך סביבו , לאחר סיום החלוקה מבצעים זאת שוב על תת המערך הימני והשמאלי. ולבסוף מחברים הכל ומקבלים מערך ממויין. כמו שאמרנו מעצם היותו אלגוריתם לאס וגאס הוא תמיד יצליח למיין אבל זמן הריצה תלוי במיקומים שנבחר.

המקרה הרע הוא מצב בו $r = 1$ או $r = n$ . בשני אלו נקבל סדרה חשבונית של מספר ההזזות שנעשה שמתחילה ב $1$ ומסתיימת ב $n$ כלומר מסתכמת ב $O (n^{2})$

המקרה טוב $a_{r}$ הוא חציון של $A$ במצב זה נקבל נוסחת נסיגה לפי משפט המאסטר שכל פעם עובדים עם חצי מערך ולכן נקבל $O (n \log n)$ .

הבחנה

לא חייב שהחלוקה תהיה בהכרח כמו במקרה הטוב כדי לקבל זמן ריצה כזה, גם אם החלוקה היא כזו שגודל כל צד הוא לפחות $\frac{n}{4}$ זמן הריצה יישאר $O (n \log n)$

מההבחנה הזאת אנחנו יכולים לבנות גרסה אחרת של האלגוריתם שנקראת מיון מהיר פרנואידי. מה שהוא עושה באופן די פשוט זה , אם לאחר חלוקה התנאי הנ״ל לא מתקיים כלומר, אם נסמן $L$ כצד הקטן יותר של $a_{r}$ ו $G$ כצד הגדול יותר, אם מתקיים $| G | < \frac{n}{4} o r | L | < \frac{n}{4}$ נבטל את בחירת הפיבוט שלנו ונחפש פיבוט חדש.

נוסחת הנסיגה של האלגוריתם הרגיל ייראה ככה

T (n) = T (| L |) + T (| G |) + O (n)

נרצה להבין מהי תוחלת זמן הריצה כלומר ה״ממוצע״ של זמן הריצה שלנו.

\begin{matrix} E [T (n)] = E [T (| L |) + T (| G |) + time to find a good pivot \cdot O (n)] = \\ E [T (L)] + E [T (G)] + E [number of times to find a pivot] \cdot O (n) \end{matrix}

$O (n)$ מייצג את מספר ההשוואות.

נשים לב שבחירת הפיבוט היא ניסוי שמבצעים שוב ושוב עד שמצליחים ולכן זה ניסוי מתפלג גיאומטרית .
נסמן את הסיכוי להצלחה כ $p$ ותוחלת מספר הניסיונות להצלחה הוא $\frac{1}{p}$ . נרצה להביא מיהו $p$ תחת ההבנה שמספר הפעמים שמחפשים פיבוט טוב הוא בממוצע $\frac{1}{p}$ .

על מנת שהפיבוט יהיה רע הוא צריך להיות או ברבע האיברים הכי קטנים או ברבע האיברים הכי גדולים. כדי שפיבוט יהיה טוב הוא צריך להיות בטווח שבין $[\frac{n}{4} + 1, \frac{3 n}{4} - 1]$ כלומר חצי מהאיברים הם טובים וחצי הם לא טובים בהסתברות שווה לבחירה פיבוט מכל מקום ולכן

p = \frac{1}{2} \to \frac{1}{p} = 2

Pasted image 20230207183537.png|450

סך הכל אם נציב ונחשב את התוחלת נקבל

E [T (n)] = O (n \log n)

Quick sort - ניתוח תוחלת זמן הריצה

נרצה לחשב את תוחלת מספר ההשוואות שכן ראינו שזאת הפעולה שמשפיעה על זמן הריצה של האלגוריתם בשלמותו כי היא זאת שמושפעת מבחירת הפיבוט. נשים לב שאנחנו לא משווים את כל האיברים אחד עם השני למשל אם שני איברים משוייכים ל $| L |$ בריצה מסויימת אז לא תבוצע השוואה שלהם אחד עם השני.
אז מתי האלגוריתם כן משווה בין $a_{i, j}$ ?
נסתכל על זה קצת אחרת

עבור

A = (a_{1}, a_{2}, \dots, a_{n})

נבנה

(y_{1}, y_{2} \dots y_{n}) | i > j \to y_{i} > y_{j}

מתי האלגוריתם משווה בין $y_{i}$ ל $y_{j}$ ? זה קורה כאשר אחד מהם נבחר להיות הפיבוט (בלי הגבלת הכלליות $y_{j} > y_{i}$ ) ועד הרגע שבו $y_{j}$ נבחר מתקיים

\forall_{k \in [i, j]} : y_{k} was not a pivot

אם אחד שכזה כן נבחר אז לא הגיוני שתהיה השוואה בינהם לכל אורך האלגוריתם שכן הם יופרדו ברגע שאחד כזה ייבחר.

נגדיר משתנה אינדיקטור

X_{i j} = {\begin{cases} 1 & y_{j} is compared with y_{i} \\ 0 & e l s e \end{cases}

נחשב את התוחלת

E [T (n)] = \sum_{i = 1}^{n - 1} \sum_{j = i + 1}^{n} E [X_{i j}]

ומתקיים מתוחלת של משתנה אינדיקטור

E [X_{i j}] = P (X_{i j} = 1)

בטווח בינהם יש $j - i + 1$ איברים וצריך לבחור 2 מבינהם ולכן

P (X_{i j} = 1) = \frac{2}{j - i + 1}

סך הכל נציב בתוחלת ונחשב נקבל

\sum_{i = 1}^{n - 1} \sum_{j = i + 1}^{n} \frac{2}{j - 1 + 1} = 2 \sum_{i = 1}^{n - 1} (\frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{n - i + 1}) < 2 \sum_{i = 1}^{n - 1} \sum_{l = 1}^{n - 1 + 1} \frac{1}{l}

= 2 \sum_{i = 1}^{n - 1} O (\ln (n - i + 1)) = O (n \log n)

מסקנה: מיון מהיר מבצע בתוחלת $O (n \log n)$ השוואות. זהו גם זמן הריצה בתוחלת.

Bucket sort

האלגוריתם הוא דטרממינסטי כאשר הקלט מיוצר בצורה אקראית.
נרצה לפתר את בעיית המיון כאשר כל מספר בקלט נבחר בהתפלגות אחידה מטווח המספרים $[0, 1]$ סה״כ נרצה לבחור $n$ מספרים.

בעזרת מיון מבוסס השוואות ניתן למיין בזמן $Ω (n \log n)$ בתוחלת. נרד מזמן זה בעזרת מיון לא מבוסס השוואות. במקרה הגרוע האלגוריתם עדיין יכול לרוץ בזמן גרוע יותר.

הרעיון נקח את טווח המספרים ונחלק ל $n$ דליים

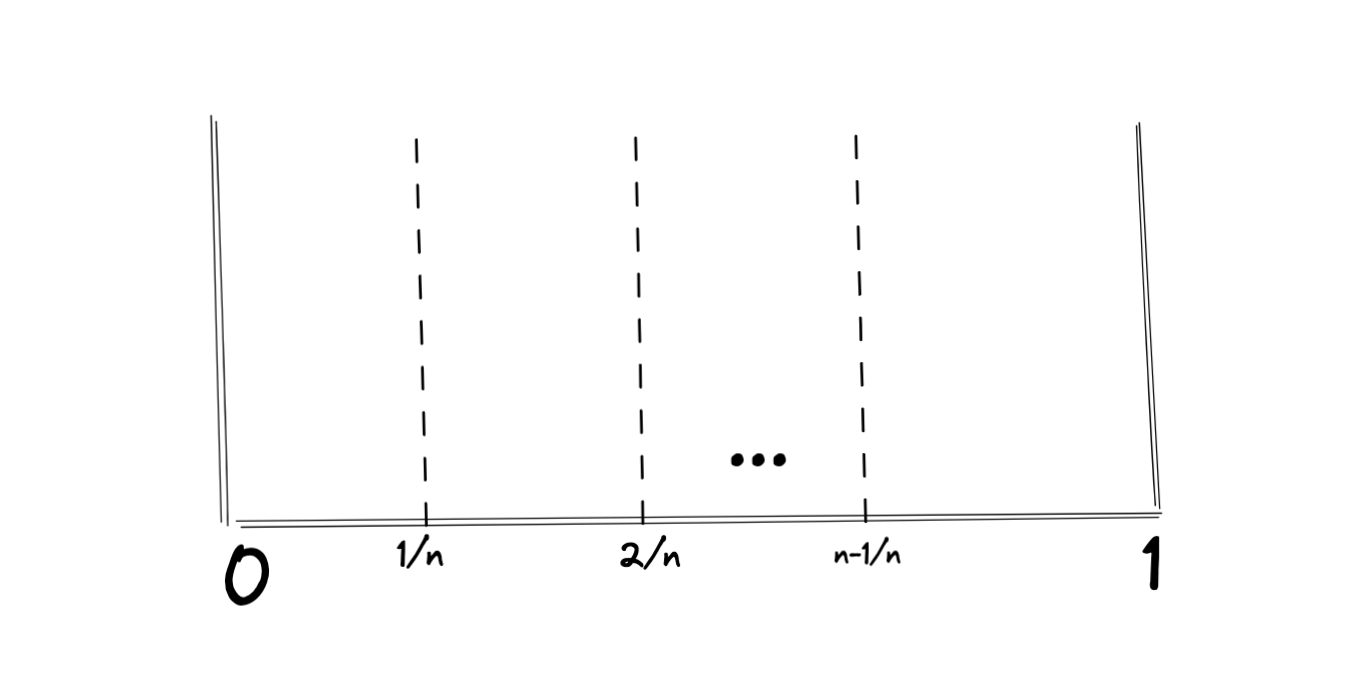
Pasted image 20230207194330.png|250

לכל איבר יש סיכוי של $\frac{1}{n}$ להיות בדלי ה $i$ כלומר תוחלת מספר האיברים בדלי הוא $n \cdot \frac{1}{n} = 1$ נובע מליניאריות התוחלת שכן נוכל להגדיר סדרת ניסויים שבתוחלת $\frac{1}{n}$ יהיו בדלי ה $i$ ואם נסכום אותם נקבל שהתוחלת של $n$ איברים להיות בדלי ה $i$ הוא הנ״ל.

אם כן אלגוריתם מיון דלי יעבוד באופן הבא:

א) נכניס כל איבר לדלי המתאים
ב) נמיין כל דלי בעזרת מיון הכנסה
ג) נשרשר את הדליים לפי סדרם

function bucketSort(array, k) 
    buckets ← new array of k empty lists
    for i = 0 to length(array) 
        insert arr[i] into the correct bucket
    for i = 0 to k 
        nextSort(buckets[i])
    return the concatenation of buckets[0], ...., buckets[k]

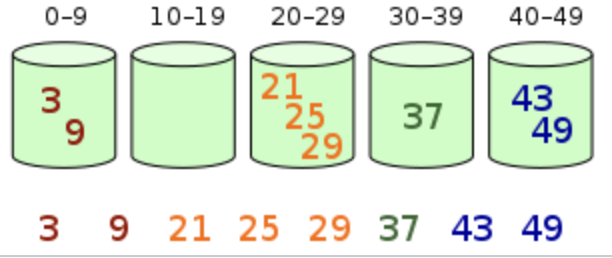
Pasted image 20230207195603.png|250

נסמן את הדלי ה $i$ כ

B_{i} = [\frac{i - 1}{n}, \frac{i}{n})

נגדיר $n_{i}$ משתנה מקרי המסמל את מספר האיברים ב $B_{i}$ ויתקיים

\forall_{i \in [n]} : E [n_{i}] = 1

זמן ריצה
הכנסה לדלי המתאים ליניארית $O (n)$
נמיין כל דלי בעזרת מיון הכנסה $O (n_{i}^{2})$
שרשור הדליים לפי סדרם $O (n)$

סך הכל

O (n + \sum_{i = 1}^{n} (n_{i})^{2})

תוחלת זמן ריצה

E [n + \sum (n_{i})^{2}] = E [n] + \sum_{} E [(n_{i})^{2}] = n + \sum_{} E [(n_{i})^{2}]

נשים לב שהאלגוריתם לוקח $n$ איברים וכל אחד מהם ״מצליח״ להכניס ל $B_{i}$ בהסתברות $\frac{1}{n}$ ו $n_{i}$ הוא משתנה מקרי שסופר את מספר ההצלחות בהסתברות $\frac{1}{n}$ להצלחה. זהו למעשה התפלגות בינומית כלומר

n_{i} \sim B (n, \frac{1}{n})

עם תוחלת $E [n_{i}] = 1$ ושונות

V a r [n_{i}] = n \cdot p (1 - p)

מהגדרת השונות אנחנו יודעים ש

1 - \frac{1}{n} = E (n_{i}^{2}) - (E [n_{i}])^{2} = E [(n_{i})^{2}] - 1 \to E [(n_{i})^{2}] = 2 - \frac{1}{n}

סה״כ נקבל

n + \sum_{} E [(n_{i})^{2}] = n + \sum (2 - \frac{1}{n}) = 3 n - 1 = O (n)

תוחלת זמן הריצה של האלגוריתם היא ליניארית בכמות האיברים במערך.

מדוע בחרנו במיון הכנסה?

הסיבה העיקרים היא שיותר קל לחסום אותו מתמטית שכן הוא ריבועי ל $n_{i}$ והסיבה השנייה היא שהציפייה היא שהגדלים של רוב הדליים יהיו קטנים יחסית מיון הכנסה מאוד טוב לגדלים קטנים.