Minimum Spanning Tree

מומלץ לקרוא את הגדרות בגרפים לפני שנכנסים לסיכום זה.

יהי $G=(V,E)$ מולטי גרף קשיר, ממושקל, עם פונקציית משקל $w:E\to \mathbb{R}$ . ויהי $T=(V,E_T)$ עץ פורש של $G$ .
נגדיר את המשקל של $T$ להיות $w(T)=\sum _{e\in E_T}w(e)$.

עץ פורש מינימלי MST של $G$ הוא עץ פורש $T=(V,E_T)$ של $G$ עם המשקל המינימלי (ייתכנו כמה כאלה).

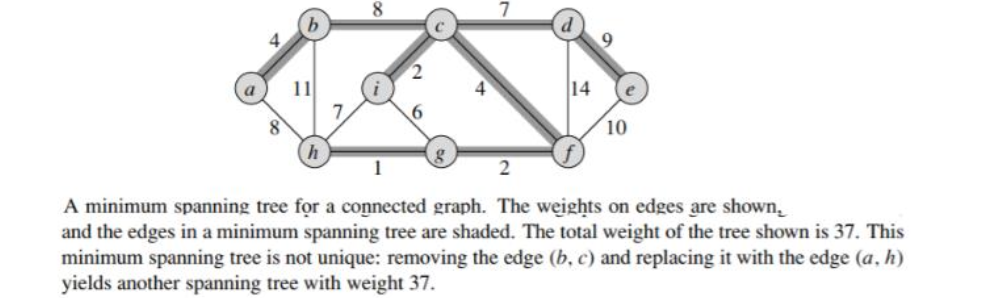
נרצה לתכנן אלגוריתם שמקבל $G$ ופונקציית משקל $w$, ומוצא עץ פורש מינימלי $T$ .
ישנם שני אלגוריתמים חמדניים שמבצעים זאת ומבוססים על אותו אלגוריתם גנרי ובחירה חמדנית.

חתך

תהי קבוצת קודקודים לא ריקה $\mathrm{\varnothing }\ne S\subset V$. החלוקה $(S,V/S)$ נקראת חתך של $G$ . והקשתות $\{e=(u,v)|u\in S,v\in V/S\}$ נקראות קשתות החתך (הן אלה שמחברות בין צד אחד לצד שני. מזכיר קצת גרף דו צדדי).

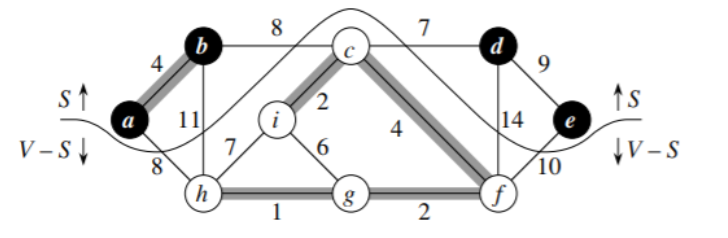
הבחירה החמדנית

יהי $G=(V,E)$ (מולטי) גרף קשיר, ממושקל, עם פונקצי׳ת משקל $w:E\to \mathbb{R}$ . עבור כל קבוצת קודקודים לא ריקה $S\subset V$, קיים עץ פורש מינימלי של $G$ , $T$ כך של $T$ מכיל את קשת החתך המינימלית בחתך $(S,V/S)$.

הוכחה
ניקח קבוצת קודקודים $S$ לא ריקה ואת החתך שנוצר איתה. ניקח את קשת החתך המינימלית נסמנה $e=(u,v)$.
יהי $T=(V,E_T)$ עץ פורש מינימלי של $G$ ונחלק למקרים:

• אם $e\in T$ סיימנו.
• אם $e\notin T$ , כיוון ש $T$ עץ, חייב להיות מסלול פשוט $P$ מ $u\to v$ ב $T$ , אנחנו יודעים שהמסלול הזה לא מכיל את הקשת $e$ , כלומר הוא עובר מצד אחד של החתך לצד השני באמצעות קשת חתך שאינה מינימלית. נסמן את הקשת הזאת $e^{\prime }=(u^{\prime },v^{\prime })$ (יכול להיות שיש עוד קשתות) אבל נגדיר שזאת הקשת הראשונה במסלול שהיא קשת חתך (מותר לנו להגדיר כאלה כי אנחנו יודעים שמספר הקשתות בחתך הוא לפחות אחד ואנחנו לא יודעים איפה הן נמצאות במסלול אז אין בעיה להגדיר את הראשונה מבינהן). כעת נוכל להסתכל על המסלול $P$ באופן הבא

$P_1$ הוא מסלול $u\to u^{\prime }$ ו $P_2$ הוא מסלול $v^{\prime }\to v$ .

כעת, נבנה גרף חדש $T^{\prime }=(V,E_{T^{\prime }})$ שמקיים $E_{T^{\prime }}=E_T\cup \{e\}-\{e^{\prime }\}$ . כלומר החלפנו את הקשת חתך הראשונה במסלול בקשת חתך המינימלית.
נרצה להראות ש $T^{\prime }$ עץ פורש מינימלי. בישביל עץ פורש מינימלי הוא צריך להיות קודם כל

1. עץ פורש
2. משקל מינימלי

עץ פורש
מהקשר של $T^{\prime }$ ל $T$ אנחנו יודעים שמתקיים ש

כלומר אם נוכיח ש $T^{ֿֿ\prime }$ קשיר אז יתקיים שהוא עץ ומהגדרה עץ פורש ל $G$ .
נוכיח שקיים מסלול בין כל שתי קודקודים $x,y$ בגרף $T^{\prime }$. אנחנו יודעים שבהכרח יש מסלול שלהם בעץ $T$ ונסמנו $P^{\prime }$ .
אם הקשת שהורדנו מ $T$ הלוא היא $e^{\prime }$ לא שייכת למסלול $P^{\prime }$ אז אותו המסלול ב $T$ הוא גם המסלול המתאים ב $T^{\prime }$ .
אחרת, $e^{\prime }\in P^{\prime }$ כלומר הורדנו חלק מהמסלול וצריך למצוא אלטרנטיבה. נניח בלי הגבלתת הכלליות ש $u$ מופיע לפני $v$ במסלול $P^{\prime }$ החדש שנבנה.
הסיבה שהוא בטוח יופיע שם היא שעכשיו הורדנו את $e^{\prime }$ מהגרף האלטרנטיבה היחידה שנוכל לתת היא עם $e$ (נשים לב שגם אין מסלול אחר שהוא לא $P^{\prime }$ כי מדובר בעץ ולא אמורים להיות בו מעגלים).
נסתכל על $P^{\prime }$ ב $T$

כאשר $P_1^{\prime }$ הוא מסלול $x\to u^{\prime }$ ו $P_2$ הוא מסלול $v^{\prime }\to y$ . אם כן נבנה את המסלול ל $T^{\prime }$ בצורה הבאה

כלומר מה שעשינו הוא ויתרנו על הקשת $e^{\prime }$ והשתמשנו במסלול ההפוך ל $P_1,P_2$ שהגדנו למעלה כך שהראשון מסתיים ב $u^{\prime }$ ואז המסלול ההופכי שלקחנו הראשון יסתיים ב $u$ ואז עם $e$ מגיעים ל $v$ ועושים את אותו תהליך (ההוכחה כך ש v לפני u היא זהה לחלוטין).
אם כן, יש מסלול מכל נקודה לנקודה ולכן הגרף קשיר וסך הכל הוא גם עץ. מהגדרת עץ פורש מתקיים שהוא פורש את הגרף $G$.

המשקל של $T^{\prime }$
נשווה בין המשקל של $T^{\prime }$ והמשקל של $T$ .
מתקיים $w(e)\le w(e^{\prime })$ כיוון ש$e$ קשת קלה יותר (המינימלית).
סך הכל יתקיים

ואמרנו ש $T$ עץ פורש מינימלי משמע $w(T)\le w(T^{\prime })$
סך הכל מחוקי אי שיוויון יתקיים

ולכן הבחירה החמדנית שאומרת שישנו עץ פורש מינימום שמכיל את הקשת הקלה בחתך נכונה.

צמצום קשתות והאלגוריתם הגנרי לעץ פורש מינימום

הצגנו את תכונת בחירה חמדנית של עצים פורשים מינימליים שנראת בסיס טוב לאלגוריתם חמדן שמוסיף ל MST בכל פעם את קשת החתך המינימלית עבור חתך כלשהו . למרות זאת , ייתכנו כאן שני קשיים :
הראשון , ההגדרה הרקורסיבית שנרצה להשתמש בה , טיפה לא ברורה , אופציה ראשונה היא למחוק קשת החתך המינימלית בחתך כלשהו מהגרף ופותרים באופן רקורסיבי עבור כל אחד משני החתכים , אבל אנחנו לא מבטיחים שאין עוד קשתות חתך שצריכות להיות בעץ הפורש המינימלי .
אופציה שניה למחוק את קשת החתך המינימלית מהגרף , אבל אחרי זה אנו צריכים שיטה להימנע ממעגלים בקשתות שבוחרים ל 𝑇𝑆𝑀.

צמצום קשתות

עבור מולטי גרף $G=(V,E)$ (יכול להיות גם גרף רגיל) וקשת $e\in E$, צמצום קשת$e=(u,v)$ נותן מולטי גרף חדש שמסומן

והוא הגרף המתקבל מ $G$ ע״י "merging" צירוף הקודקוד $u,v$ לקודקוד אחד בשם $uv$ כלומר

כעת נגדיר פונקצייה שממירה קודקוד גרף לקודקוד בגרף המצוצמם באופן הבא

סך הכל נוכל להגדיר את קבוצת הקשתות של הגרף המצומצם כך

נשים לב שבגלל שאנחנו עובדים עם גרף לא מכוון אז אין לולאות עצמיות. כמו כן תכונת הצמצום מאפשרת לנו לדעת בוודאות שלא יווצר מעגל כתוצאה מהצמצום בגלל שאין לולאות עצמיות.

כעת התכונה הזאת מאפשרת לנו לבנות את האלגוריתם הגנרי הבא

MST-Generic(G=(V,E),w) 
	while |V|>1
		let e be the minimum weight edge of some cut in G
		add e to E_t
		conrtract e
	return E_t	

נשים לב שזה אלגוריתם גנרי ולא מימוש מלא. ישנם שתי אלגוריתמים שהם מימוש של הנ״ל והם נבדלים באיך שהם בוחרים את החתך. בחירה זו משנה את זמן הריצה.

הוכחת תת המבנה האופטימלי לאלגוריתם הגנרי

יהי $G=(V,E)$ מולטי גרף קשיר ממושקל עם פונקציית משקל $w$ .
ויהי $(S,V/S)$ חתך של $G$ ותהי $e=(u,v)$ קשת חתך מינימלית.
תהי $T^{\prime }=(V/e,E_{T^{\prime }})$ עץ פורש מינימלי של $G/e$ .
אזי, $T=(V,E_T)$ כאשר $E_T=E_{T^{\prime }}\cup \{e\}$ הוא עפ״מ של $G$.

עץ פורש
ראשית נרצה להוכיח $|E_T|=|V|-1$ . נשים לב ש $T^{\prime }$ עפ״מ ולכן

אבל $$|E_{T}|=|E_{T^{\prime}}|+1= |V|-2+1= |V|-1$$
כעת הוכחנו שבהינתן שהוא גרף קשיר אז הוא עץ.
נוכיח שהוא קשיר, בהינתן שתי קודקודים $x,y$ נמצא את המסלול בינהם.
נפעיל את פונקציית הצמצום $f$ עליהם כיוון ש $T^{\prime }$ הוא עפ״מ שהוא גם צמצום של $T$ . אם לאחר הפעלת $f$ נקבל שתי קודקודים שהמסלול שלהם ב $T^{\prime }$ לא עובר ב $uv$ אז אותו המסלול יעבוד גם ב $T$.
אחרת הפתרון לבעיה הוא פשוט. כל מסלול שעובר בקודקוד $uv$ יעבור עכשיו בקשת $(u,v)$. לכן $T$ קשיר, הוא גם עץ וגם קשתותיו מוכלות בקשתות של $G$ כלומר הוא עץ פורש של $G$.

משקל מינימלי
נב״ש ש $T$ אינו עץ פורש מינימלי של $G$ .
ניקח $\bar{T}=(V,\bar{E})$ עפ״מ של $G$ כלומר $w(\bar{T})<w(T)$. מתכונת הבחירה החמדנית נוכל להניח ש $e\in \bar{E}$ .
כעת ניקח ${\bar{T}}^{\prime }=(V/e,E_{{\bar{T}}^{\prime }})$ כאשר $E_{\bar{T}}^{\prime }=E_{\bar{T}}/\{e\}$. כלומר צמצמו את הקשת המינימלית בחתך של העץ החדש.
נשים לב ש ${\bar{T}}^{\prime }$ הוא עפ״מ של $G/e$ כי

1. $$|E_{\overline{T^{\prime }}}|=|E_{\bar{T}}|-1=(|V|-1)-1=|V/e|-1$$
2. לכל זוג קודקודים בגרף המצוצמם אם המסלול $P$ בינהם משתמש ב $e$ אז בצמצום זה הפך להיות קודקוד אז המסלול עדיין קביל פשוט במקום לעבור בקשת של הגרף הוא עובר בקודקוד חדש, אחרת , אותו מסלול $P$ קיים גם בגרף המצומצם.
3. $E_{\overline{T^{\prime }}}\subseteq E$

קיבלנו סך הכל

קיבלנו

אבל $T^{\prime }$ הוא עפ״מ באותו גרף מצומצם בסתירה לכך ש $T^{\prime }$ הוא עפ״מ .

סה״כ קיבלנו שבנייה של עפ״מ באופן ריקורסיבי על ידי הוספת קשת חתך מינימלי לתת עץ פורש מינימלי משאירה אותו מינימלי ולכן תכונת תת המבנה האופטימלית מתקיימת.

prim algorithm

הרעיון באלגוריתם פרים הוא להסתכל על החתך $(S,V/S)$ כאשר $S$ הוא קודקוד יחיד. באופן הזה האלגוריתם מסתכל שוב ושוב על קשת החתך המינימלי שנוגעת בקודקוד היחיד ב$S$ ומצמצם את הגרף מקשת זו.
על מנת לשלוט ביעילות האלגוריתם, הקודקוד ב $S$ נבחר להיות הקודקוד החדש המצוצמם שהתקבל מצמום קשת החתך המינימלית האחרונה. נשים לב שבאיטרציה הראשונה בוחרים קודקוד שרירותי .
ז״א שאם יש קשת חתך שלא הצטמצמה , אז הקשת תהיה החתך הבא.
בגלל שמתסכלים רק על קשתות החתך, אנחנו נמנעים מסריקת כל הקשתות בכל איטרציה. אף על פי כן, צמצום קשת יכול להוסיף קשתות חדשות לחתך הבא.
כיוון שהגרף הוא מולטי גרף ייתכנו כמה קשתות בין אותם קודקודים כאשר לכל קשת מששקל שונה, אבל כיוון שמחפשים קשת חתך מינימלית בכל פעם, נוכל פשוט לשמור מידע עבור הקשת המינימלית בין זוג קודקודים.

באופן סכימתי האלגוריתם ייראה ככה:

1. יצירת קבוצה שמאכלסת את כל הקשתות ב עץ פורש מינימלי. היא מתחילה כקבוצה ריקה.
2. לכל קודקוד נוסיף מידע $p$ שמייצג את הקודקוד אליו הוא מקושר בחתך $S$ ונוסיף ערך key שמייצג את המשקל אמ״מ הוא קשת חתך עם $S$ אחרת יהיה שם $\mathrm{\infty }$ . כמו כן באופן שרירותי ניקח קודקוד אחת וניתן לו מפתח $0$
3. מאתחלים תור קדימויות עם קודקודי $V$ נסמנה $Q$, יחס הסדר הוא לפי ערכי המפתחות.
4. כל עוד התור לא ריק נוציא את המינימום $u$ ונבדוק האם הוא מקושר ל $S$ או לא כלומר האם $p$ לא ריק (במילים אחרות נשאלת השאלה האם היא קשת חתך או לא)
5. אם הוא לא ריק אז מוסיפים אותו ל$E_T$ כי הוא הקשת חתך המינימלית
6. רצים על כל השכנים של $u$ בלי קשר להאם הוספנו אותו ל $E_T$ ובודקים האם שכן $v$ נמצא בתור Q וגם המשקל שלו עם $u$ קטן מ $v.key$ כלומר האם המשקל שלו עם u קטן מהמשקל שלו עם הקודקוד בחתך $S$ .
7. אם התנאי מתקיים משנים את ערך המפתח של $v$ להיות המשקל שלו עם $u$ ואת $p$ של $v$

נשים לב לשתי דברים חשובים

1. הקודקוד הראשון $r$ תמיד יצא באיטרצייה הראשונה.
2. אנחנו לעולם לא נבחר קודקוד שכבר משוייך ל $S$ אחרת יהיה מעגל וזה בסתירה להגדרת העץ. זה נעשה על ידי הבדיקה האם השכן קיים בערימת מינימום.

ההצטמצמיות מבוצעות ע"י תור 𝑄 כאשר ערך ה- keys לכל קודקוד 𝑢 הוא המשקל של הקשת עם משקל מינימלי שמקשרת בין 𝑢 לקודקוים שנמחקו מ- 𝑄 . באתחול , כל ה- keys להיות ∞ . חוץ מהקודקוד השרירותו r שנבחר לראשונה , המפתח שלו הוא 0 בהתחלה . בנוסף מאתחלים Q להכיל את כל 𝑉 . וכך , הקודקוד הראשון שמוחקים מ- 𝑄 הוא 𝑟 , ואז מעדכנים את המפתחות לכל השכנים של 𝑟 להיות המשקל של הקשת ביניהם לבין 𝑟 . מהאיטרציה השניה והלאה , האינטרפרטציה צריכה להיות שכל הקודקודים שנמחקו מ- Q הצמצמו לקודקוד אחד. וכך , המפתח הקטן ביותר לקודקודים שעדיין ב- 𝑄 מייצגים את הקשת המינימלית שמקשרת אותם לקודקוד היחיד שהוצמצם . ולכן , האלגוריתם מוציא את הקודקוד 𝑢 עם המפתח עם המפתח הקטן ביותר ומוחק 𝑢 מהתור 𝑄. האינטרפרטציה היא שקשת חתך מינימלית מתווספת ל- 𝑇𝑆𝑀. על מנת לבצע צמצום של קשת חדשה שבחרנו להכנה לאיטרציה הקודמת , האלגוריתם סורק את כל השכנים של 𝑢 לבדוק אם המפתח שלו צריך הפחתה , עקב כניסת קשת חדשה לחתך.

MST-PRIM(G=(V,E),w)
	E_T = empty_set
	for each u in V 
		u.key = INFINITY
		u.p = NULL
	set r.key = 0 for some arbitrary r in V

	Q.init(V)
	while |Q| >= 1
		u = Q.extract_min()
		if u.p != NULL
			E_T.add(u,u.p)
		for each v in u.ADJ()
			if Q.contains(v) and weight(u,v)< v.key
				v.key = weight(u,v)
				v.p = u
	return E_T				

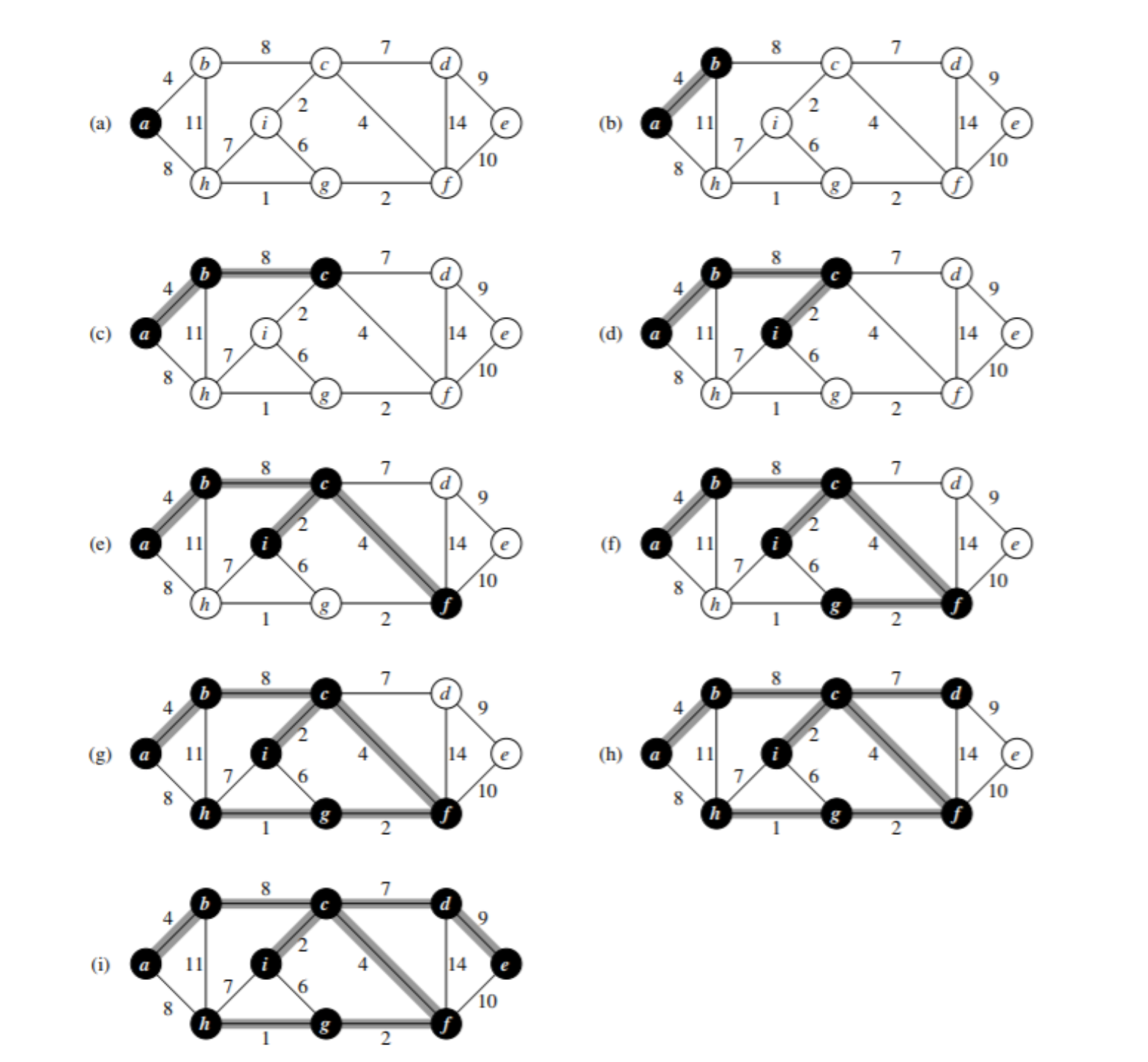
זמן ריצה
זמן הריצה תלוי גם באימפלמנטצייה של $Q$ נסכם בטבלה (ניתן לממש גם באופן אחר ואפילו מומלץ במקרים מסויימים למשל אם המשקלים מוגבלים בגודל או שהם בינאריים)

Kruskal algorithm

כדי להבין את האלגוריתם של prim מומלץ לעבור קודם על Union find .

הרעיון של האלגוריתם הזה הוא למצוא את הקשת המינימלית בגרף המצומצם ולהוסיף את הקשת הזו ל MST.
המימוש יעבוד כך:

1. מיון הקשתות לפי המשקלים.
2. סריקתם מהמינימום למקסימום
3. על כל קשת $e$ נבדוק האם הקשת מייצרת מעגל עם קבוצת הקשתות שכבר הוספנו ל MST
4. אם היא מייצרת מעגל לא מכניסים אותה, אחרת מכניסים ל MST.

נשים לב שעל מנת לבדוק האם $e$ מייצרת מעגל עלינו להשתמש במבנה נתונים Union Find שמצויין למעלה. כך נוכל לייצג את הרכיבים הקשירים של הקשתות שכבר נבחרו ל MST.
נזכיר שהפעולות שמבנה נתונים זה תומך הן make_set ו find_sey ו union על קבוצות מופרדות.
$e=(u,v)$ תייצר מעגל אמ״מ find_set(u)=find_set(v) .

MIST-Kruskal(G=(V,E),w)
	E_T = empty_set
	for each u in V
		make set(u)
	sort(E by w)
	for each e = (u,v) in E 
		if find_set(u) != find_set(v)
			E_T.add(e = (u,v))
			union(u,v)
	return E_T		 

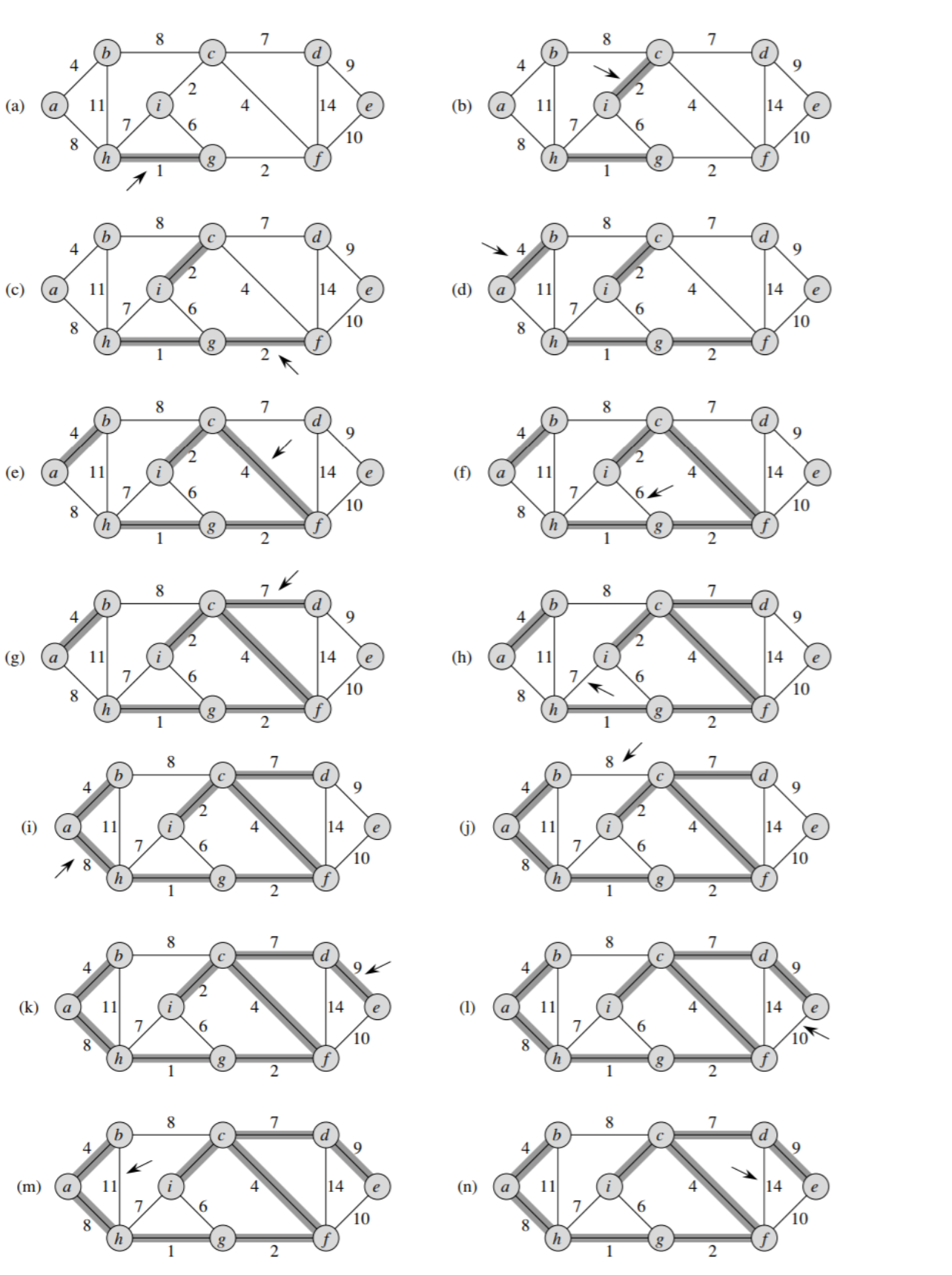
זמן ריצה
במבנה נתונים union_find פעולת make_set לוקחת $O(1)$ זמן ופעולת find_set ופעולת union לוקחות $O(\alpha |V|)$ זמן ממוצע, כאשר $\alpha |V|$ היא inverse Ackerman funcion . האלגוריתם ממיין את הקשתות של $E$ ואז מבצע $2|E|$ פעולות find ו $|V|-1$ פעולות union. סה״כ

כלומר זה תלוי כמה זמן לוקח למיין את E.