Divide and conquer

בהגדרה - הפרד ומשול זוהי פרדיגמה לתכנון אלגוריתם המשתמשת בריקורסיה על מנת להפוך בעייה קלה לבעיות קלות יותר , זאת באה עם היתרונות והחסרונות שלה , למשל אנחנו עלולים לחשב מספר ערכים , מספר רב של פעמים כפי שנראה ב תכנות דינמי.
הרעיון מאחורי הפרדיגמה של הפרד ומשול היא פשוטה ואומרת :

• תפריד את הבעיה לבעיות קטנות יותר (הפרד).
• תפתור את הבעיות הקטנות יותר(משול).
• מזג את התוצאות.

היכולת הזאת לפשט את הבעיה מאפשרת לנו לפתור בעיות ביעילות ריצה שלא היינו מגיעים אליה בתכנות לא רקורסיבי.

כעת נראה מספר בעיות הניתנות לפתרון בעזרת ריקורסייה.

מינימום ומקסימום

מינימום

נניח שיש לנו מערך $A[n]$ (האלמנטים יכולים להיות מכל סוג כל עוד יכולת ההשוואה מוגדרת על אותו הסוג). ננסה למצוא את איבר המינימום של המערך הזה

הפתרון הטריוויאלי העולה בראש של כל מתכנת, היא להחזיר משתנה מקומי $min$ ולשמור אליו את הערך המינימלי תוך כדי ריצה על המערך. או בתיאור פסודו:

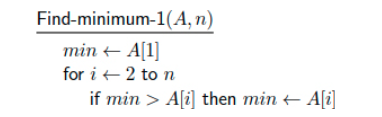
עם זאת אנחנו נאלץ לבצע $n-1$ השוואות ונרוץ על כל המערך, לא נשמע כזה נורא אך ניתן לפתור את זה אחרת .

נוכל אולי לבטא את $n$ כביטוי בחזקת $2$ למשל $2^m$ ונוכל לחלק את המערך שלנו לזוגות (אולי יישאר איבר בודד אבל זה לא משנה), נשווה כל זוג והמנצח ממשיך לשלב הבא ככה עד שנשאר איבר אחר (מעין טורניר בודוקאי).

בפסודו:

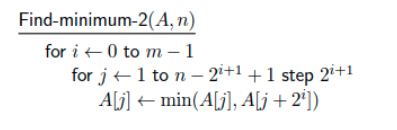
נשים לב שאנחנו רוצים לזוז כל פעם בקפיצות ביחס לקומה בה אנחנו נמצאים ככל ש i מתקדם ככה יש פחות ופחות איברים במערך , על מנת שלא נקצה עוד זכרון נרוץ בקפיצות המתוארות למעלה.
באופן ויזואלי :

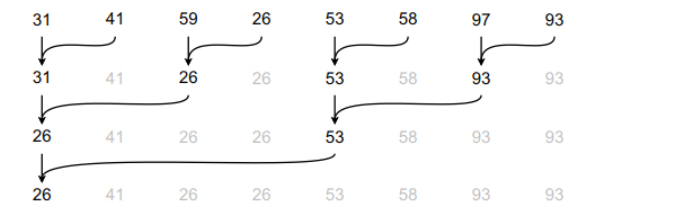
האם שיפרנו משהו? עבדנו קצת קשה אבל סך הכל נראה ש נקבל

נשאלת השאלה, האם הדבר במקרה?

לכל שיטה בה נבחר אנחנו תמיד נצטרך לעבור על $n$ האיברים במערך כדי לדעת האם האיבר עליו אנחנו עומדים הוא המינימום או לא. כלומר אנחנו תמיד נמצא את עצמנו בונים מעין עץ בינארי שלם לכל השוואה שנבחר וכפי שנדבר בהמשך ,

לכל עץ בינארי עם $n$ עלים, יש בידיוק $n-1$ קודקודים פנימיים.
לכן על מנת למצוא את המינימום נצטרך לעשות $n-1$ השוואות, לא ניתן לייעול.

מקסימום

נשמע שזאת אותה הבעיה לא? פשוט להחליף את הסימן (להחליף $\le$ ב $\ge$ ).
המעבר בין בעיה א׳ לבעיה ב׳ הוא אלגוריתם בפני עצמו הנקרא reduction , זהו כלי בסיסי אך אפשר לדבר עליו רבות.

במקרה הזה המעבר די פשוט והוא עוזר לנו גם לדעת שנדרשת $n-1$ פעולות על מנת למצוא את המקסימום.

מינימום ומקסימום ביחד

נוכל פשוט לחבר את שתי התוכנות לפעולה אחת ולקבל את התוצאה ב $2n-2$ שהיא חסומה ב $O(n-1)$ כמו השיטות הקודמות .

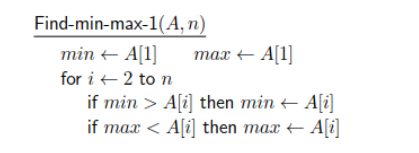
אבל בואו ננסה לייעל את השיטה הזאת ,
דרך אחת תהיהי להוסיף $else$ בין שני ההשוואות כי כמובן שאם אחת מתקיימת השנייה לא. במערך עולה ממויין עם זאת, עדיין נקבל $2n-2$ פעולות. לא רע במיוחד אבל נוכל לייעל .

כעת, סוף סוף נוכל לדבר ולהראות איך נשתמש ב הפרד ומשול כדי לפתור בעיות,

הפעולה תחזיר $(M,m)$ אחד מייצג את המקסימום ואחד את המינימום (לתוהים ששואלים איך אפשר להחזיר דבר כזה בתכנות, פשוט בונים struct , class או tuple).

הפרד - נחלק את המערך לחצי כל פעם - תנאי העצירה יהיה כאשר גודל תת המערך הוא 2 ואז נוכל להחזיר השוואה רגילה .

משול - על כל תת מערך שמאלי וימני נפעיל רקורסיבית את הפעולה שוב פעם.

מזג - נחזיר את המקסימום בין $M_{1,2}$ כאשר $1$ זה תת המערך השמאלי ו $2$ זה תת המערך הימני. באופן דומה נחזיר את המינימום בין $m_1,m_2$ .

Algorithm: Max - Min(x, y)
if y – x ≤ 1 then
return (max(numbers[x], numbers[y]), min((numbers[x], numbers[y]))
else
(max1, min1):= maxmin(x, ⌊((x + y)/2)⌋)
(max2, min2):= maxmin(⌊((x + y)/2) + 1)⌋,y)
return (max(max1, max2), min(min1, min2))

נחשב את זמן הריצה :
עבור $n$ שקטן או שווה ל$2$ אז זמן הריצה זהו זמן ריצה קבוע , לכן מה שמעניין זה כאשר $n>2$ .

צמצמנו את זמן הריצה אבל זה לא ממש נחשב שיפור, וזה בלי לקחת בחשבון את העובדה שהריקורסייה תופסת יותר זכרון ואולי בכלל עדיף את הקוד הליניארי והשימוש בלולאה כמו מקודם... אבל עדיין זאת דרך לעבוד עם הפרד ומשול.

מיון מיזוג

הצורך להחזיק אוסף מסוייף בסדר כלשהו הוא צורך תמידי הניכר בכל תחומי חיינו, גם בתכנות הרבה מאוד פעמים נרצה את המידע שלנו בסדר כלשהו. השיטה הטירוויאלית שכולם מכירים bubble sort היא המוכרת מכולם והפשוטה מכולם אך היא לוקחת $\mathrm{\Omega }(n^2)$ השוואות.

באלגוריתם מיון המיזוג נשתמש בהפרד ומשול כדי לייעל את זמן המיזוג שלנו:

הפרד - כל פעם נחלק את המערך לשני חצאים.

משול - ברגע שנגיע למערך בגודל 2 נחליף את סדר האיברים בהתאם לגודלם

מיזוג - לאחר שסידרנו כל תת מערך נחבר את החלקים למערך אחד גדול וממויין.

קוד המיזוג יהיה מאוד נאיבי כמובן שצריך לדעת באיזה אופן למזג וזה לא מספיק סתם לחבר בין שני המערכים, ישנם מספר דרכים למזג בין מערכים לא אפרט את כל התהליך כי זה לא רלוונטי , חשוב לדעת שכולן בסך הכל לוקחות $O(n)$ מבחינת זמן ריצה
מצרף פה כמה אימפלמנטציות אפשריות :

TOP - DOWN

// Split A[] into 2 runs, sort both runs into B[], merge both runs from B[] to A[]
// iBegin is inclusive; iEnd is exclusive (A[iEnd] is not in the set).
void TopDownSplitMerge(B[], iBegin, iEnd, A[])
{
    if (iEnd - iBegin <= 1)                    // if run size == 1
        return;                              // consider it sorted
    // split the run longer than 1 item into halves
    iMiddle = (iEnd + iBegin) / 2;          // iMiddle = mid point
    // recursively sort both runs from array A[] into B[]
    TopDownSplitMerge(A, iBegin,  iMiddle, B);  // sort the left  run
    TopDownSplitMerge(A, iMiddle,    iEnd, B);  // sort the right run
    // merge the resulting runs from array B[] into A[]
    TopDownMerge(B, iBegin, iMiddle, iEnd, A);
}

//  Left source half is A[ iBegin:iMiddle-1].
// Right source half is A[iMiddle:iEnd-1   ].
// Result is            B[ iBegin:iEnd-1   ].
void TopDownMerge(A[], iBegin, iMiddle, iEnd, B[])
{
    i = iBegin, j = iMiddle;
 
    // While there are elements in the left or right runs...
    for (k = iBegin; k < iEnd; k++) {
    // If left run head exists and is <= existing right run head.
        if (i < iMiddle && (j >= iEnd || A[i] <= A[j])) {
            B[k] = A[i];
            i = i + 1;
        } else {
            B[k] = A[j];
            j = j + 1;
        }
    }
}

BOTTOM - UP

//  Left run is A[iLeft :iRight-1].
// Right run is A[iRight:iEnd-1  ].
void BottomUpMerge(A[], iLeft, iRight, iEnd, B[])
{
    i = iLeft, j = iRight;
    // While there are elements in the left or right runs...
    for (k = iLeft; k < iEnd; k++) {
   // If left run head exists and is <= existing right run head.
        if (i < iRight && (j >= iEnd || A[i] <= A[j])) {
            B[k] = A[i];
            i = i + 1;
        } else {
            B[k] = A[j];
            j = j + 1;    
        }
    } 
}

סך הכל הפסודו קוד יהיה מהצורה של אלגוריתם המיון יהיה מהצורה

ננתח את הסיבכויות זמן ריצה לפי שיטת המאסטר

לפי שיטת המאסטר נקבל שמספר הפעולות הריקורסיבי שווה למספר הפעולות הלא ריקורסיביות ולכן

(הבסיס הדיפולטי בסיכום זה יהיה 2 תמיד, רשמתי את זה פה רק כדי שיהיה ברור).

אנקדוטה - כל אלגוריתם מיון על מידע שכל מה שידוע עליו הוא יחס הסדר תמיד יהיה חסום ב $O(nlogn)$.

כפל של מספרים גדולים

על פניו נשמע כמו כותרת מוזרה כי תכנותית אנחנו רושמים פשוט
$\text{return }x\cdot y$

אז מה זה אומר בכלל ? נסתכל על הבעיה באופן תיאורטי ונניח שגודל המספר יכול להיות אין סופי , למרות שבמעבדי 64 ביטים הייצוג המקסימלי של מספר מספיק לרוב הבעיות שאנחנו מתמודדים איתם, נרצה להבין תיאורטית איך ניתן לייעל כפל כזה בהינתן שאנחנו מקבלים קלטים בגדלים לא ידועים השואפים למספר אינסופי.

יהי $X,Y$ שני מספרים ששניהם באורך $n$ ביטים (כלומר בייצוג הבינארי שלהם). נניח את אורך הביטים בלי הגבלת הכלליות כיוון שאם נרצה להקטין מספר פשוט נשים כמה 0 שצריך מה msb .

אז איך בכלל מתחילים לחשב זמן ריצה של דבר כזה? שלא לדבר על איך משתמשים בהפרד ומשול כדי לחשב את זה ... לפי החוקים של כפל אנחנו בעצם נבצע $n^2$ פעולות כפל וחיבור באלגוריתם הנאיבי ולכן חסום ב $\mathrm{\Theta }(n^2)$ .

זה בשיטה הנאיבית. ננסה לראות כמה יצא לנו על ידי שימוש בהפרד ומשול
נגדיר $X=x_1{x}_2{x}_3\dots x_n$ וגם $Y=y_1{y}_2{y}_3\dots y_n$. כאשר כל ספרה שייכת לקבוצה הבינארית וכל ספרה היא ביט.

נחלק באמצע את מספר הספרות באופן הבא

כעת כמו שניתן לפרק מספר לספרות בבסיס 10 נעשה זאת על המספרים שלנו באופן הבא

הכפל בינהם יהיה

וכאן בעצם יש לנו איזשהי זהות ריקורסיבית וזהות זאת תהיה המשול שלנו, על כל תתי מספרים בינאריים ניקח את החצאים וננחשב רקורסיבית את הביטוי המתמטי הזה.

בפסודו קוד זה ייראה ככה :

ומבחינת סיבוכיות זמן ריצה נקבל

כאשר $cn$ מייצג את כל הפעולות הלא ריקורסיביות כמו העלאת חזקה וכל פעולות החיבור שנעשה.
לפי שיטת המאסטר נקבל שהסיבוכיות הזאת היא גם כן $\mathrm{\Theta }(n^2)$ וזה לא עזר. נוכל לייעל את הזמן ריצה הזה אך לא בהרבה על ידי כך שנשים לב שמתקיים

נסמן $A=X_1{Y}_1$ ו $B=X_2{Y}_2$

כלומר באמצע החישוב של $A,B$ נוכל לייצר תלות עם הביטוי האמצעי ולחסור פעולה ריקורסיבית אחת, נקבל זמן ריצה קצת יותר יעיל של $n^{1.5}$ .
המסקנה היא שצריך לדעת מתי להשתמש בהפרד ומשול כי לא בהכרח שזה יהיה שווה את זה.ֿ

אנדקוטה , פעולת העלאה בחזקת n של מספר בשיטת הפרד ומשול היא לוגריתמית ביחס ל n.