#data_structures

Disjoint Set Data Structure

בהינתן עולם כלשהו של איברים אנחנו רוצים להחזיק חלוקה של האיברים הללו לקבוצות זרות.
כל איבר מתחיל כקבוצה בפני עצמו וניתן לאחר שתי קבוצות לקבוצה גדולה ללא אפשרות פיצול.

Disjoint set או Union find הוא מבנה נתונים התומך בפעולות הבאות

make-set(x) יוצר קבוצה עם האיבר החדש $x$ .
union(x,y) מאחד בין שתי קבוצות המכילות את האיברים $x, y$ (בהנחה שהן בשתי קבוצות שונות)
find-set(x) מוצא את הקבוצה שלה איבר $x$ שייך (נשים לב ש $x$ הוא מצביע לאיזשהו איבר בקבוצה כלשהי)

מימוש ברשימה מקושרת

נחזיק רשימה מקושרת דו כיוונית לכל קבוצה ונגדיר לכל קבוצה איבר מזהה הנציג.
באופן הזה נוכל להפעיל את union בזמן קבוע כי נחזיק לכל רשימה מצביע לראש ולזנב, כלומר אם union יופעל על $x, y$ בסדר הזה, ניקח את הזנב של הקבוצה שבה $x$ נמצא, ונחבר ל נציג של הקבוצה שבה $y$ נמצא
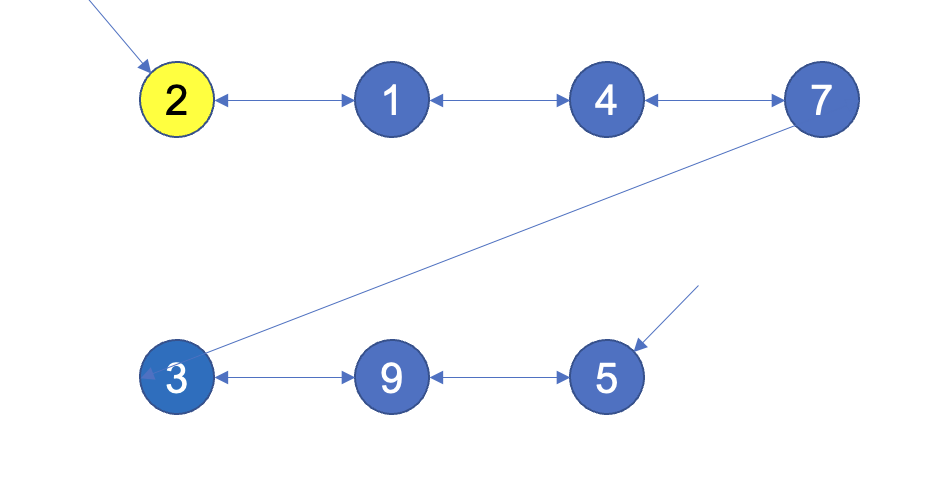
Pasted image 20221128171853.png|250

החישוב של find-set פשוט ידרוש מאיתנו ללכת עד לראש הרשימה כלומר $O (n)$ זמן. בהנחה, (לא סבירה) שהאיחוד נעשה תמיד על הנציגים של הקבוצות. במקרה הכללי, דרוש לפני כן למצוא את הנציגים בשתי קריאות ל find-set כלומר $O (n)$ .

אם נרשום את זמני הריצה בטבלה זה ייראה ככה

make-set	union	find-set
O(1)	O(1)	O(n)

ייעול לרשימה מקושרת

כל איבר יחזיק מצביע לאיבר הראשון ברשימה וכעת נוכל לגשת לנציג בזמן ריצה קבוע.
הבעיה שנוצרת ברעיון הזה היא שבמיזוג שתי קבוצות נצטרך להשקיע הרבה יותר זמן כדי לעדכן את המצביעים של רשימה אחת להצביע על ראש הרשימה השנייה (כמובן שנעדיף לקחת את הרשימה הקצרה יותר אבל עדיין זמן הריצה בודק את המקרה הגרוע שהוא $O (n)$ ) /
Pasted image 20221128172346.png|350

כלומר אם נרשום את זמני הריצה כעת זה ייראה ככה

make-set	union	find-set
O(1)	O(n)	O(1)

נשים לב ש union בפועל לוקח $O (m i n (| S_{x} |, | S_{y} |))$ שבמקרה הגרוע זה שקול ל $n$ .

ב ניתוח לשיעורין העלות לשיעורין של פעולת union היא $O (\log n)$

מימוש על ידי יערות

נחזיק יער של כל הקבוצות, כאשר כל קבוצה תייצג רכיב קשירות ביער כלומר עץ כאשר השורש הוא ה נציג שהגדרנו.

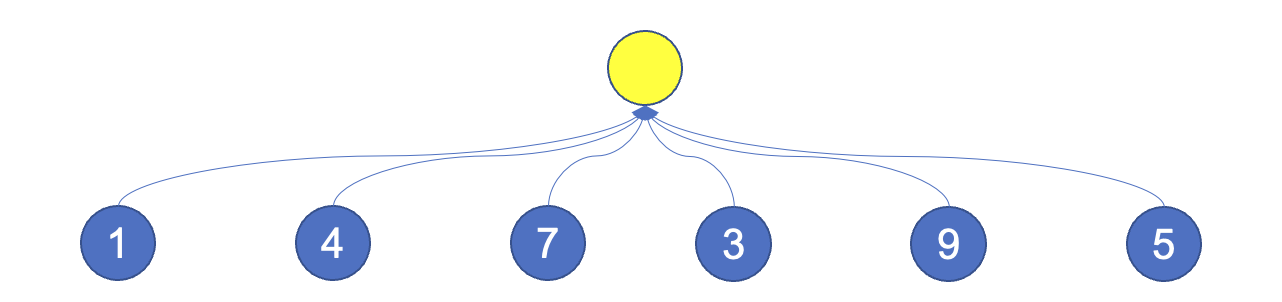
Pasted image 20221128173323.png|350

לכל קודקוד $x$ נשמור מצביע לאבא שלו בעץ , האבא של הנציג יהיה עצמו. וכעת
find-set(x) פעולה החסומה בגובה העץ.
make-set(x) יצירת שורש חדש שיצביע לעצמו
union(x,y) ניקח את העץ בעל הגובה הקטן ביותר להיות בן של העץ בעל הגובה הגדול ביותר . נשייך לכל קודקוד דרגה rank שמייצגת את הגובה של הקודקוד (ביחס לתת העץ המושרש בו כלומר מהו הגובה של העץ כאשר הקודקוד הוא השורש)

find-set(x)
	if parent(x) != x
		find-set(x)
	return x	

make-set(x)
	x.parent = x
	x.rank = 0

union(x,y)
	x = find-set(x)
	y = find-set(y)
	child = min_root(rank(x), rank(y))
	parent = max_root(rank(x), rank(y))
	parent.add-child(child)

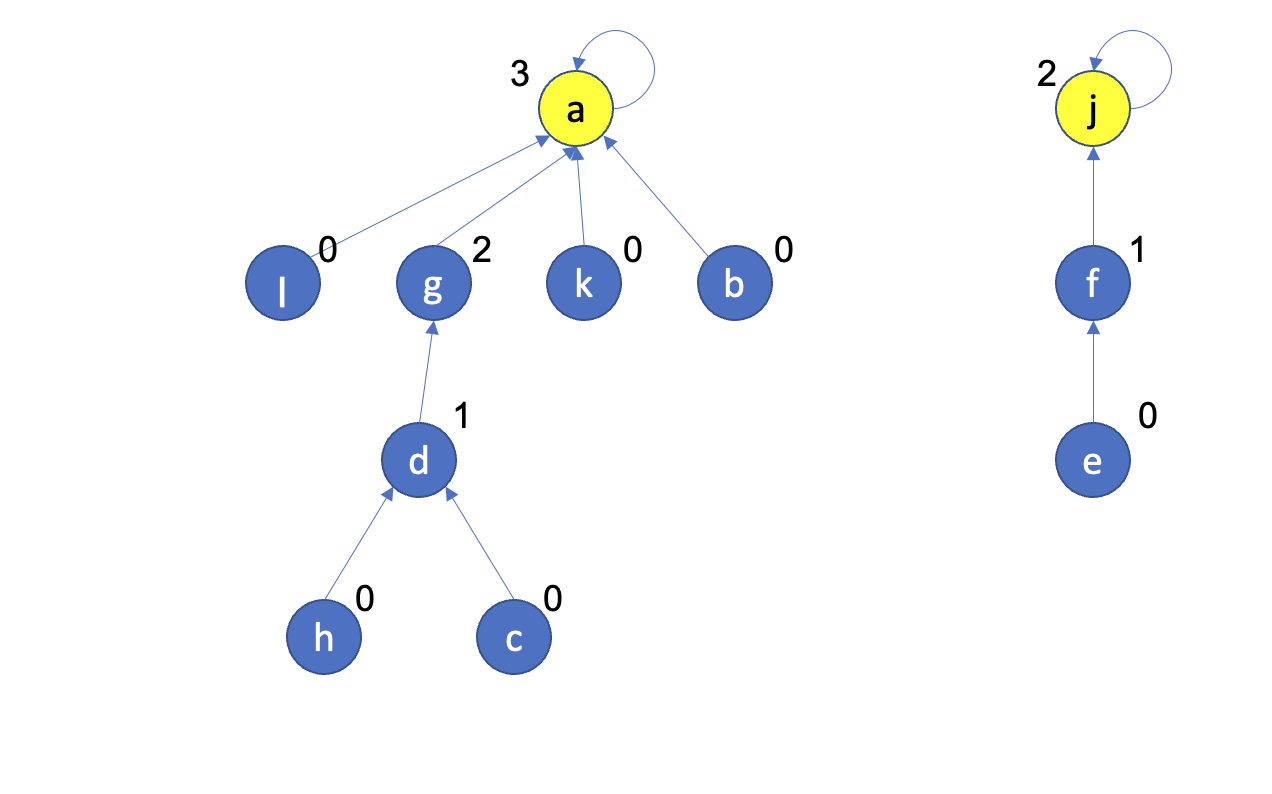
Pasted image 20221128181141.png|350
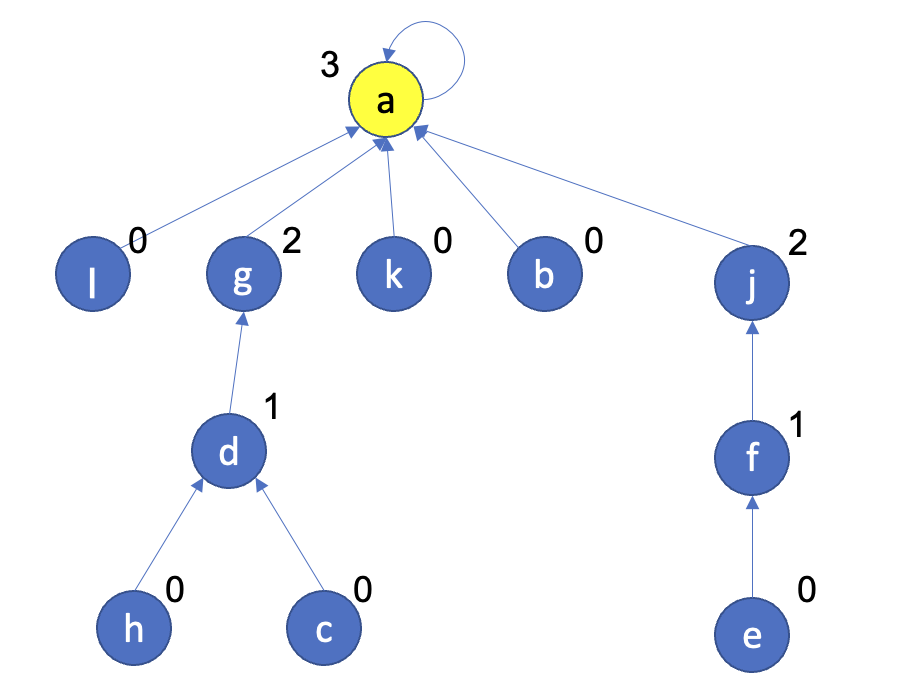
Pasted image 20221128181205.png|350
נשים לב, ה rank של כל הקודקודים נשאר זהה, פרט למקרה שבו מאחדים שני עצים עם אותו rank, ואז השורש החדש מקדם את הrank ב1.

דחיסת מסלולים

אם אנחנו משקיעים $O (x)$ זמן כדי לשלוף ערך מסויים $t$ אז בסוף הפעולה נהפוך את עומק $x$ להיות $1$ ע״י הגדרת $t$ כבן ישיר של השורש.
את התהליך הזה נעשה לכל הקודקודים על המסלול מ $x$ עד לשורש.

int find_set(int v) {
    if (v == parent[v])
        return v;
    return parent[v] = find_set(parent[v]);
}

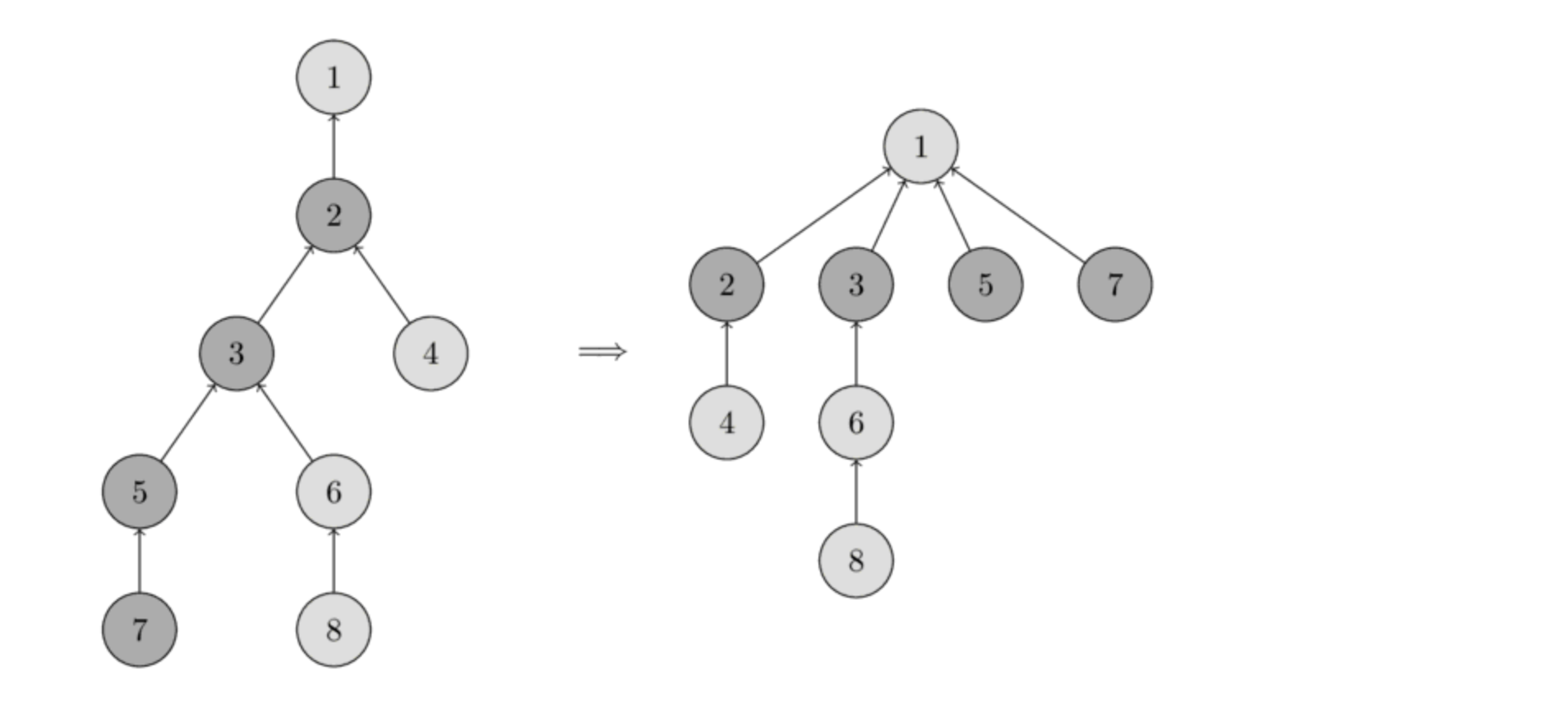
Pasted image 20221128201253.png|450
נשים לב שאין צורך לעדכן את ה rank של קודקודים שאינם מעודכנים, גם ככה משתמשים רק ב rank של השורש לביצוע union. גם אם הדרגה של השורש תפסיק לייצג את גובה העץ ממש, היא עדיין תהיה חסם עליון על גובה העץ.
(בפועל זה יכול לגרום למצב שנאחד עץ גבוה לתוך עץ נמוך, בכל מקרה זמן הריצה עדיין חסום בצורה טובה).

תכונות

לכל $x$ שאינו השורש מתקיים $r a n k (x) < r a n k (π (x))$ נשים לב ש $π$ מייצג את האבא של קודקוד $x$ .
ההוכחה תחולק למקרים
א. אם יוצרים קודקוד אז בוודאי שמתקיים כי $x$ הוא שורש.
ב. אם התקיים עבור $x$ עד לזמן מסויים, יכול להשתנות רק כתוצאה מהבאים
שינוי $r a n k (x)$ , שינוי $π (x)$ או שינוי של $r a n k (π (x))$ ללא שינוי של $π (x)$ .

הראשון לא משתנה לעולם אם $x$ הוא לא השורש, כי ביקשנו שהאלגוריתם לא ישנה את זה.
השני יכול להשתנות רק במצב שבו $x$ היה שורש ואוחד בפעולת union או שהוא השתנה כתוצאה מדחיסת מסלולים , בשתי המקרים האבא עדיין עם דרגה גבוהה יותר.
השלישי קורה רק בתהליך של גדילה ולכן לא יכול להיות מצב שהיחס הזה ישתנה.

לכל שורש עם rank שערכו k יש עץ עם לפחות $2^{k}$ קודקודים
ההוכחה היא באינדוקצייה על מספר פעולות ה union כי אלה היחידות שמשנות את הדרגה.
בסיס: אם לא עשינו פעולת union אחת הדרגה בהכרח שווה ל 0 ובעץ יש לכל הפחות קודקוד אחד $2^{0} = 1$ .
צעד: נניח שמתקיים לפני הביצוע של union בפעם ה n. נסמן את הדרגה לפני ב $r_{1}$ ואת הדרגה אחרי הפעולה ב $r_{2}$ ובאופן דומה נסמן ב $s_{1}, s_{2}$ את גדלי העצים לפני ואחרי הפעולה.

אם $r_{1} (x) \neq r_{1} (y)$ ובלי הגבלת הכלליות נניח $r_{1} (x) < r_{1} (y)$ אז $y$ יהיהי שורש העץ החדש

\begin{matrix} s_{2} (y) = s_{1} (x) + s_{1} (y) \geq 2^{r_{1} (x)} + 2^{r_{1} (y)} \geq 2^{r_{1} (y)} = 2^{r_{2} (y)} \end{matrix}

אם $r_{1} (x) = r_{1} (y)$ ובלי הגבלת הכלליות נניח $y$ יהיהי שורש העץ החדש אזי

s_{2} (y) = s_{1} (x) + s_{2} (y) \geq 2^{r_{1} (x)} + 2^{r_{1} (y)} = 2^{r_{1} (x) + 1} = 2^{r_{2} (x)}

לכל קודקוד שדרגתו $k$ , ניתן לשייך קבוצה של לפחות $2^{k}$ קודקודים שונים כך שכל קודקוד במבנה יהיה משוייך לכל היותר לקודקוד אחד שדרגתו k

אם יש $n$ איברים ביעד בסה״כ אז יש לכל היותר $\frac{n}{2^{k}}$ קודקודים עם דרגה $k$

זמני ריצה

בסדרה של $m$ פעולות על מבנה הנתונים שמכיל $n$ איברים העלות הכוללת תהיה
$O (n \log^{*} n + m \log^{*} n) \subseteq O (m \log^{*} n)$
נזכיר ש $\log^{*}$ זה בעצם כמה פעמים ניתן להוציא log עד שמגיעים למספר קטן או שווה ל1.

T (n) = T (\log n) + 1

שימושים

מציאת מעגלים בגרף לא מכוון

1. Create disjoint sets for each vertex of the graph.  
2. For every edge u, v in the graph  
    i) Find the root of the sets to which elements u and v belongs.  
    ii) If both u and v have the same root in disjoint sets, a cycle found.