תמורה היא פונקצייה חח״ע ועל
דוגמה לתמורה מעל
נסמן אותה כ
דרכים מקובלות לסמן תמורה
כפונקצייה:
כמחזורים זרים :
אדגים זאת כאן אבל פירוט נוסף נמצא בהסבר על חבורת התמורות
למשל עבור התמורה
נוכל לסמן אותה גם כ
זה בעצם סימון שמפריד את התמורה לחלקים שקוראים אחד לשני...
חילופי סדר
בתמורה ישנו מצב של חילוף סדר שמשמעו
דרכים למציאת חילופי הסדר
מעקב אחרי הערכים (זאת שיטה פחות יעילה):
למשל עבור
| 1<2 | 1<3 | 2<3 |
|---|---|---|
ולכן מספר חילופי הסדר בתמורה הוא
השיטה הציורית
- נכתוב את התמורה כפונקצייה ונעביר ״קו״ בין מספרים שווים
- נספור את החיתוכים שנוצרו לנו ואלו מספר חילופי הסדר
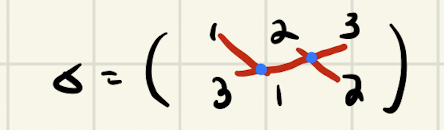
סימן התמורה
לכל תמורה יש סימן התלוי במספר חילופי הסדר, נסמן את מספר חילופי הסדר ב
תמורה תקרא זוגית אם
הגדרה נוספת לסימן התמורה :
נגדיר את סימן התמורה
למשל עבור התמורה
יתקיים